Lernpfad Lineare Gleichungssysteme - Alles rund um Freizeit
In diesem Lernpfad lernst du, was lineare Gleichungssysteme (LGS) sind und welche Verfahren zur Lösung es gibt. Zu den verschiedenen Lösungsverfahren wirst du selbst Videos erstellen. Zudem wirst du Anwendungssituationen zu linearen Gleichungssystemen kennenlernen.
Die Übungen im Buch beziehen sich auf das Schülerbuch "Schnittpunkt Mathematik 9 - Differenzierende Ausgabe" des Klett-Verlages.
Die Aufgabe kann mit einer Gleichung mit zwei Variablen gelöst werden. Die Variable x steht für den Preis einer Tüte Pommes, die Variable y für den Preis einer Dose Cola.
Löse durch Probieren
Die obige Situation lässt sich durch die Gleichung x + 2y = 5 beschreiben. Finde durch Probieren verschiedene Zahlenpaare (x;y), die diese Gleichung erfüllen. Wie viel könnten eine Tüte Pommes und eine Dose Cola kosten, damit die Gleichung passt? Notiere deine Werte in einer Tabelle.
Die Gleichung für die Situation oben lautet x + 2y = 5.
Alle Zahlenpaare (x;y), die diese lineare Gleichung erfüllen, sind Lösungen der Gleichung. Diese Lösungen stellen Punkte (xy) im Koordinatensystem dar und liegen auf der Geraden mit der Funktionsgleichung y=mx+b.
Übung 1 Text - Gleichung (online)
Ordne im Quiz und in der nachfolgenden LearningApp dem Text eine passende Gleichung mit zwei Variablen und eine mögliche Lösung zu.
Addiert man zu einer Zahl 6, so erhält man das Dreifache der anderen Zahl.
Addiert man zur zweiten Zahl 6, so erhält man das Vierfache der ersten Zahl.
Die Summe zweier Zahlen ist 52.
Das Doppelte der ersten ist gleich dem Dreifachen der zweiten Zahl.
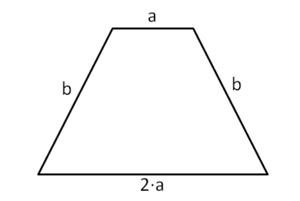
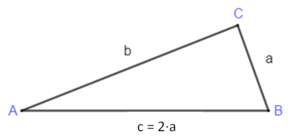
Ein gleichschenkliges Dreieck hat einen Umfang von 41 cm.
In einem gleichschenkligen Dreieck ist die Basis (Grundseite) nur ein Drittel so lang wie die Schenkel.
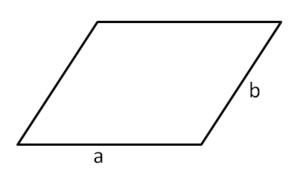
Der Umfang eines Rechtecks ist 80 cm.
Der Flächeninhalt eines Rechtecks beträgt 64cm².
Andreas hat 6 CDs mehr als Karin.
x + y = 522x + y = 41y = xy + 6 = 4∙xx + 6 = 3∙yx∙y = 642∙x = 3∙yy = x - 62x + 2y = 80
Übung 2 Text - Gleichung (Buch)
Löse die Aufgaben aus dem Buch. Gib zunächst die Bedeutung der Variablen an und stelle anschließend die Gleichung auf.
Löse in drei Schritten:
1. Bedeutung der Variablen angeben:
x Anzahl der 2er Gruppen
y Anzahl der 3er Gruppen
2. Gleichung aufstellen:
x·2 +y·3 = 24
3. Mögliche Lösungen angeben:
Setze für x eine mögliche Zahl ein und berechne dann den zugehörigen y-Wert. Wenn du z.B. 3 Zweiergruppe bildest, sind schon 6 Schüler:innen eingeteilt, es bleiben also 18 Schüler:innen übrig. Diese kannst du in 6 Dreiergruppen einteilen. Eine mögliche Lösung ist also (3;6). Finde so mögliche Werte, die du für x und y einsetzen kannst durch Ausprobieren.
(3;6); (6;4); ...
Löse die übrigen Teilaufgaben ebenso in drei Schritten!
1. Bedeutung der Variablen angeben:
x eine Zahl
y eine andere Zahl
2. Gleichung aufstellen:
x+y=9
3. Mögliche Lösung angeben (probiere aus):
(0;9); (1;8); ...
Löse die übrigen Teilaufgaben ebenso in drei Schritten!
1. Bedeutung der Variablen angeben:
x eine Zahl
y eine zweite Zahl
2. Gleichung aufstellen:
"Die Summe" bedeutet "+"
"Dreifaches einer zweiten Zahl" bedeutet "3·y"
1. Bedeutung der Variablen angeben:
x eine Zahl
y eine andere Zahl
2. Gleichung aufstellen:
"Die Differenz" bedeutet "-"
"dem Dreifachen einer Zahl" bedeutet ...
"dem Doppelten einer anderen Zahl" bedeutet ...
Gleichung: ... - ... = 7
3. Mögliche Lösungen
Finde durch Probieren mögliche Lösungen, die du für x bzw. y einsetzen kannst.
Bei geometrischen Anwendungen hilft immer ein Skizze! Zeichne die angegebene Figur und beschrifte sie passend zur Aufgabenstellung. Gib die Bedeutung der Variablen an! Finde durch Probieren mindestens zwei Lösungen.
Betrachte als Hilfe die Skizze links, das Kantenmodell. a ist die Seitenlänge aller Seiten des gleichseitigen Dreiecks, c ist die Höhe des Prismas. Wenn du dieses Kantenmodell basteln sollst, wie viele Spieße der Länge a benötigst du und wie viele der Länge c. Die Summe beträgt dann 60 cm.
Betrachte als Hilfe die Skizze rechts, das Kantenmodell der quadratischen Pyramide. Stelle einen Term für die Kantenlänge auf. Diese soll dann 40 cm betragen.
Die Gleichung ist im Aufgabentext gegeben.
a) Setze in die Gleichung für x den Wert 1 ein und berechne damit den Wert für y:
y = -4x+3 für x=1
y = -4· 1+3 (Tipp: Zwischen -4 und x muss ein Malzeichen ergänzt werden.)
y = -1
(1|-1)
Die Gleichung ist im Aufgabentext gegeben.
Bei d und e ist der Wert für y gegeben. Setze hier für y ein und löse die Gleichung nach x auf.
y = -4x+3 für y=4 4y=-4·x+3 |-3
1 = -4·x | :(-4)
- = x
(-0,25|4)
Wenn du den Graphen einer linearen Funktion zeichnen möchtest, kannst du dies schnell mithilfe der Steigung m und des y-Achsenabschnitts b. Daher wandle die Gleichungen in die Form y = mx + b um.
a) y - 2x = 5 |+2x
y = 2x + 5
Diese Gerade kannst du nun in ein Koordinatensystem zeichnen. (Steigung m = 2 und y-Achsenabschnitt b = 5)
Wie zeichne ich eine Gerade mit m und b?
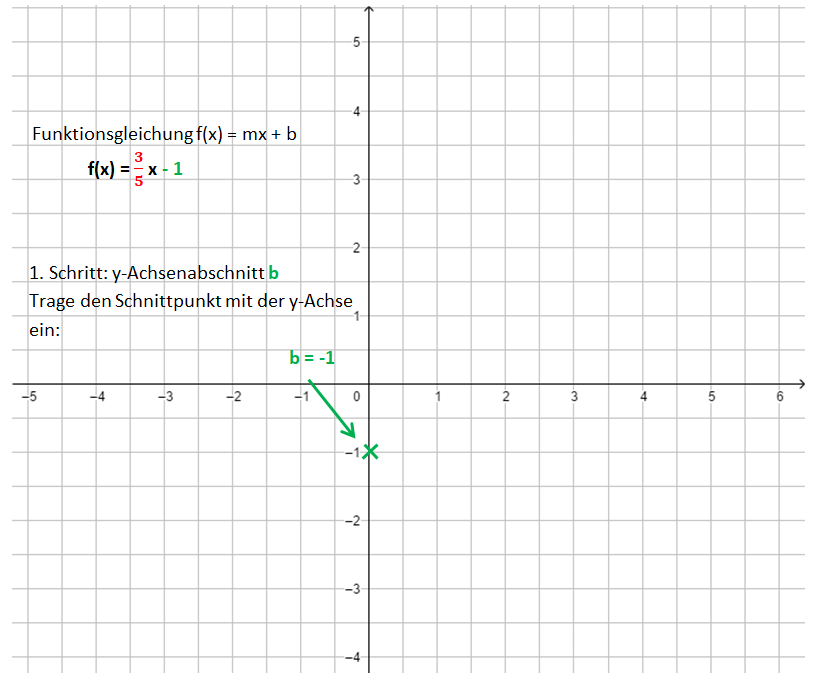
1. Schritt: Zeichne den y-Achsenabschnitt b ein: P(0|b)
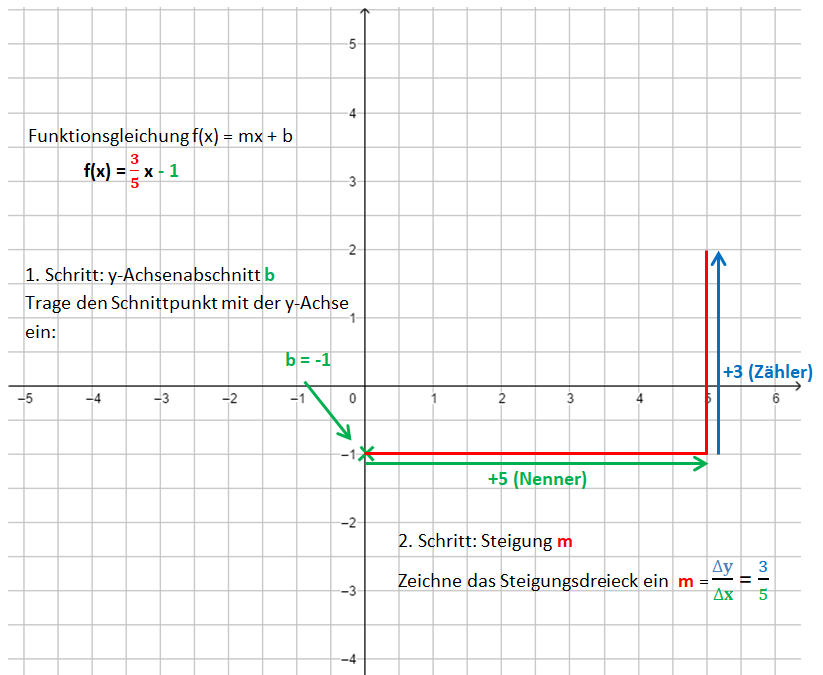
2. Schritt: Zeichne das Steigungsdreieck ein. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten).
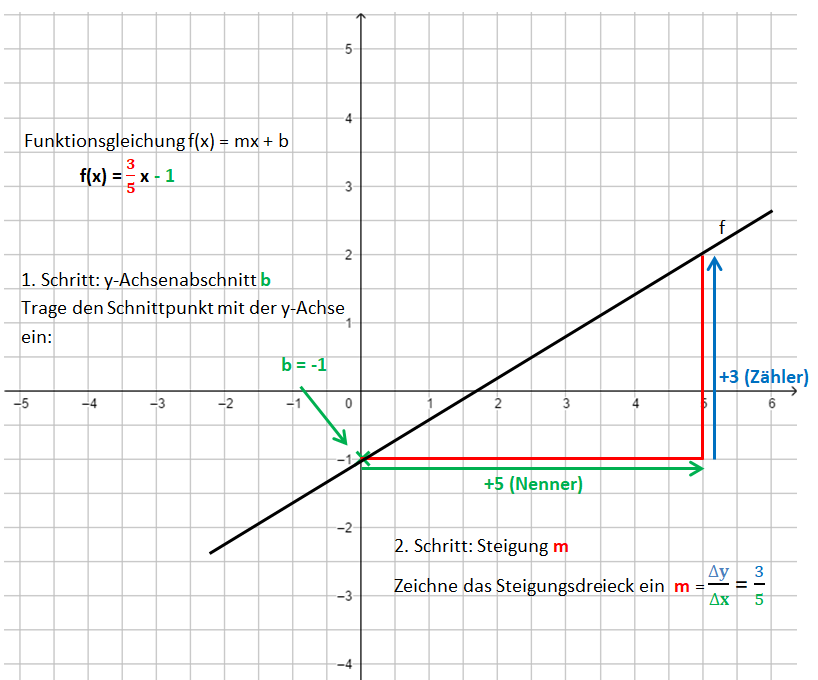
3. Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Punktprobe: Setze für x und y in der Gleichung die angegebenen Werte des Punktes ein und prüfe, ob eine wahre oder falsche Aussage entsteht.
Bei einer wahren Aussage (w) erfüllt der Punkt die Gleichung und liegt auf dem Graphen, bei einer falschen Aussage (f) nicht.
a) 2x-3y+3=0 Prüfe (4;2)
2·4-3·2+3=0 |Rechne die linke und rechte Seite aus.
8-6+3=0
5=0 (f), also erfüllt der Punkt die Gleichung nicht.
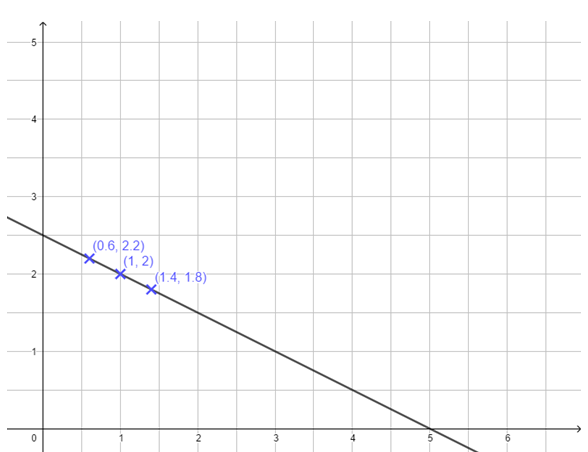
Forme die Gleichungen um in die Form y = mx + b und zeichne die zugehörigen Geraden in ein Koordinatenkreuz. Zeichne die Punkte ebenfalls in das Koordinatenkreuz. Lies ab, welcher Punkt auf welcher Geraden liegt.
Beispiel:
2x - 3y + 3 = 0 |-2x; -3
-3y = -2x - 3 |:(-3)
y = x + 1
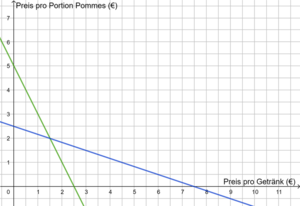
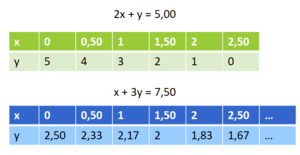
Lege die Bedeutung der Variablen fest, z.B. x - Preis pro Getränk, y - Preis pro Portion Pommes. Stelle nun jeweils eine passende Gleichung auf. Nutze zur Lösung verschiedene Darstellungen: Wertetabellen und Graphen
Ein lineares Gleichungssystem (LGS) besteht aus zwei linearen Gleichungen. Diese haben jeweils zwei Variablen. Das Wertepaar (x;y), das beide Gleichungen erfüllt, ist die Lösung des linearen Gleichungssystems. Diese Lösung kannst du z.B. durch Probieren erhalten (Wertetabelle).
Cookies helfen uns bei der Bereitstellung von ZUM Projektwiki. Durch die Nutzung von ZUM Projektwiki erklärst du dich damit einverstanden, dass wir Cookies speichern.
