Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2) Lineare Funktionen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
K (Maria Eirich verschob die Seite 2) Lineare Funktionen nach Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2) Lineare Funktionen) |
(kein Unterschied)
| |
Version vom 12. April 2020, 21:34 Uhr
2.1) Lineare Funktionen erkennen und darstellen
Im Aktiv-Urlaub warten verschiedene Aufgaben auf die Klassen.
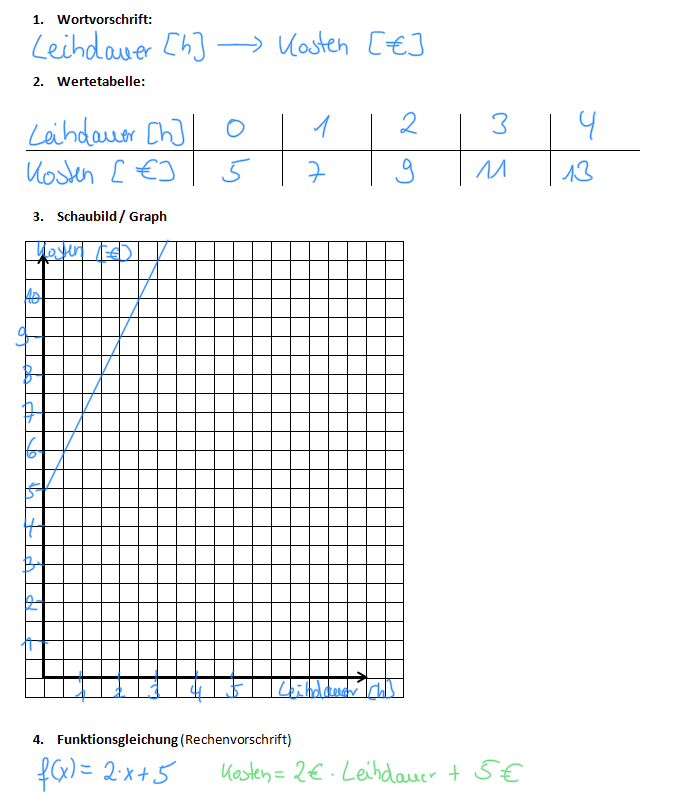
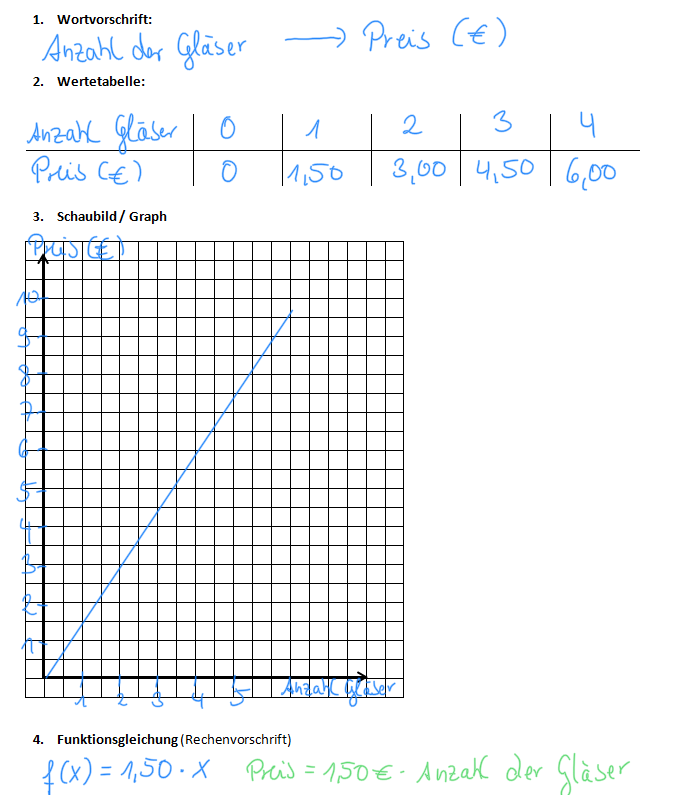
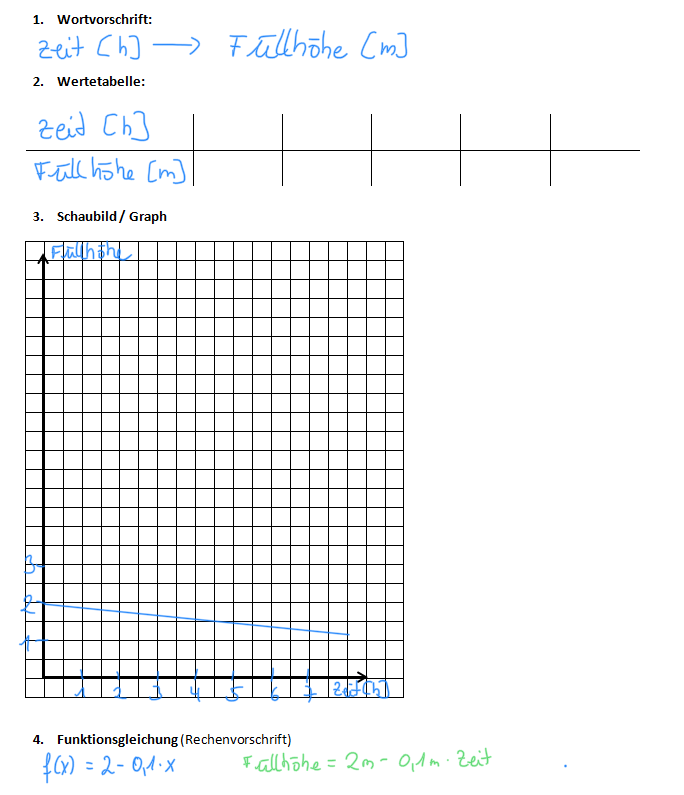
Welche Zuordnung liegt vor? Der Leihdauer x (in h) werden die Kosten y (in €) zugeordnet. Erstellen eine Wertetabelle für 0,1,2,... Stunden und zeichne den Graphen.
Vergleiche die Graphen mit denen der Wanderung. Fällt dir etwas auf?
Diese Eigenschaften werden in folgendem Lied besungen (hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen). Du musst noch nicht jeden Zusammenhang, der hier genannt wird, verstehen. Vieles davon erarbeitest du auf den nächsten Seiten.
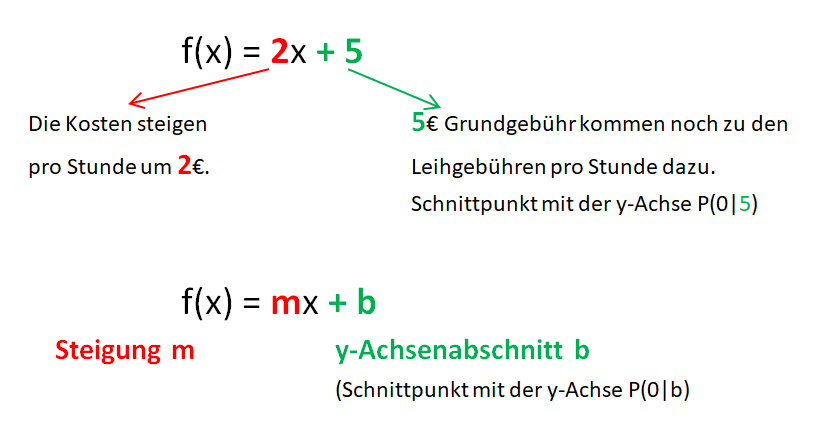
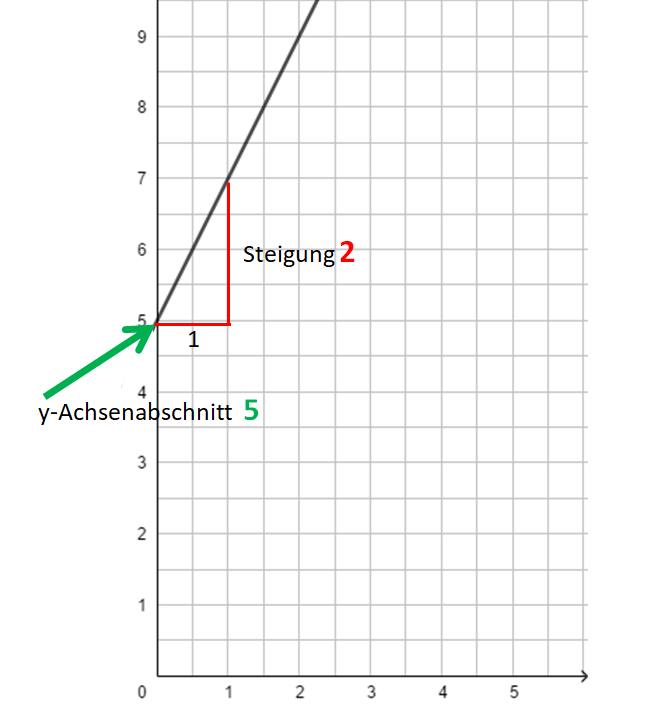
2.2 f(x) = mx + b: Bedeutung von m und b der Funktionsgleichung
Damit du einen Eindruck von der Bedeutung m (Steigung) und b (y-Achsenabschnitt) erhältst, verändere in der folgenden Animation mithilfe der Schieberegler die Größe von m und b. Notiere deine Beobachtungen stichpunktartig.