|
|
| (64 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| {{Box|1=Info |2=In diesem Lernpfadkapitel kannst du etwas über '''Punkte und Vektoren im Raum''' lernen und wirst erfahren, was Schrägbilder und Netze von geometrischen Körpern sind und wie du sie zeichnen kannst. Ebenfalls erwartet dich in diesem Kapitel, was unmögliche Figuren sind und woran du diese erkennen kannst. Dir stehen eine Vielzahl an verschiedenen Aufgaben zum Üben zur Verfügung. | | {{Box|1=Info |
| | |2= In diesem Lernpfadkapitel beschäftigst du dich mit '''Punkten und Vektoren im Raum'''. |
| | Du lernst die Grundlagen zum Thema Punkte und Vektoren. Dies Beinhaltet die Unterscheidung dieser beiden Begriffe, das Rechnen, Interpretieren und Anwenden im Sachzusammenhang. |
|
| |
|
| Bei den Aufgaben unterscheiden wir folgende Typen:
| | Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen: |
|
| |
|
| *In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | | * Mit Aufgaben, die <span style="color: #F19E4F"> '''orange''' </span> gefärbt sind, kannst du <span style="color:#F19E4F">'''grundlegende Kompetenzen'''</span> wiederholen und vertiefen. |
| | * Aufgaben in <span style="color: #5E43A5"> '''blauer''' </span> Farbe sind Aufgaben <span style="color: #5E43A5">'''mittlerer Schwierigkeit'''</span> |
| | * und Aufgaben mit <span style="color: #89C64A"> '''grünem''' </span> Streifen sind <span style="color: #89C64A">'''Knobelaufgaben'''</span>. |
|
| |
|
| *Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''.
| | Wir wünschen dir viel Erfolg! |
| | | |3=Kurzinfo}} |
| *Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''.
| |
| | |
| | |
| Viel Erfolg!|3=Kurzinfo}}
| |
|
| |
|
| ==Wiederholung von Punkten und Vektoren== | | ==Wiederholung von Punkten und Vektoren== |
| {{Box|Erinnerung: Punkte und Vektoren im Raum|{{Lösung versteckt|1= Diesdas Lennarts machts|2=Infobox|3=Einklappen}}| | | {{Box | 1=Merksatz |2= Jeder Punkt lässt sich durch den Vektor beschreiben, der den Ursprung auf diesen Punkt verschiebt, den '''Ortsvektor'''. Bei Punkten werden die Koordinaten direkt an den Namen des Punktes geschrieben, der Name des Punktes wird immer groß geschrieben; bei Vektoren, also auch bei Ortsvektoren, werden die Koordinaten durch ein Gleichheitszeichen vom Namen des Vektors getrennt, der Name des Vektors wird manchmal mit einem Pfeil darüber versehen und meistens klein geschrieben. |
| Merksatz}}
| |
|
| |
|
| ==Das dreidimensionale Koordinatensystem== | | Zum Punkt <math>A(1|2|3) </math> gehört also der Ortsvektor <math>\vec {a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix} </math>.|3= Merksatz}} |
|
| |
|
| | ==Koordinatensystem== |
| | {{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben. |
|
| |
|
| | #Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3. |
| | #Zeichne die Punkte <math> A (1|2|1)</math>,<math> B(1|4|2)</math>, <math> C(1|2|{-}1{,}5)</math> und <math> D(1|4|{-}0{,}5) </math> in das gezeichnete Koordinatensystem. Zeichne nun die Verbindungsvektoren <math>\vec{ AB }</math> , <math>\vec{ AC }</math>,<math>\vec{ CD }</math> und <math>\vec{ BD }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. |
| | #Nutze den Punkt <math> A (1|2|1)</math> aus Aufgabenteil 2. Füge die Punkte <math> E (-1|2|1)</math>,<math> F(1|0|1)</math>, <math> G(-1|0|1)</math> und <math> H(0|1|5) </math>. Zeichne nun die Verbindungsvektoren <math>\vec{ AE }</math>,<math>\vec{ AF }</math>, <math>\vec{ AH }</math>, <math>\vec{ EG }</math>, <math>\vec{ FG }</math>, <math>\vec{ FH }</math> , <math>\vec{ EH }</math> und <math>\vec{ GH }</math> ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn. |
|
| |
|
| | |
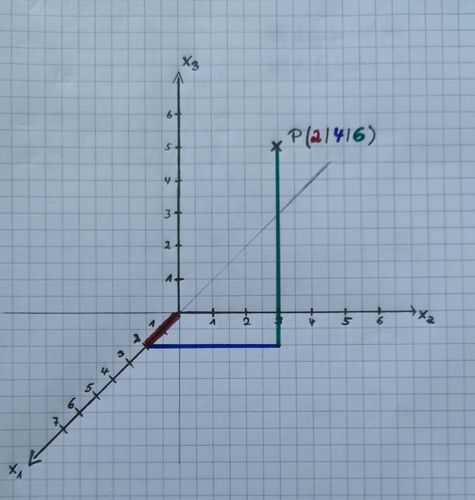
| | {{Lösung versteckt|1= Punkte in einem dreidimensionalen Koordinatensystem kannst du mithilfe eines "Pfad-Folge-Verfahren" genau bestimmen. Dabei geht man die durch die Punktkoordinaten angegeben Längeneinheiten in die Richtung der jeweiligen Achsen. Es entsteht einen Koordinatenzug. Das folgende Bild verdeutlicht das Verfahren. |
|
| |
|
| | [[Datei:Koordinatenzug.jpg|rahmenlos|500x500px|Koordinatenzug des Pfad-Folge-Verfahrens]] |
| | |2= Tipp|3=Einklappen}} |
|
| |
|
|
| |
|
| {{Box|Erinnerung: Bekannte Körper|{{Lösung versteckt|1=[[Datei:Schrägbild eines Würfels.svg|alternativtext=Würfel|mini|106x106px]]
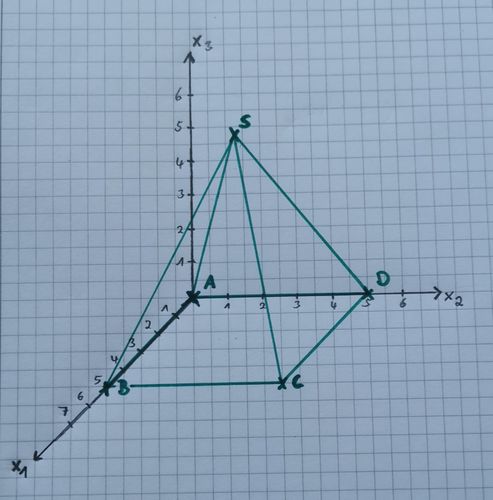
| | {{Lösung versteckt|1= Bei Aufgabenteil 2 handelt es sich um ein Parallelogram. Bei Aufgabenteil 3 bekommst du eine Pyramide heraus, die eine quadratische Grundfläche besitzt. Deine Lösung kann aufgrund einer anderen Skalierung der Achsen natürlich auch von der folgenden Lösung abweichen. |
| Der '''Würfel''' besteht aus sechs gleichgroßen Flächen. Zudem besitzt der Würfel 12 gleichlange Kanten und acht Ecken.<br />
| | [[Datei:Lösung 2,3.jpg|rahmenlos|500x500px|Lösung]] |2= Lösung|3=Einklappen}} |
|
| |
|
| | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} |
|
| |
|
|
| |
|
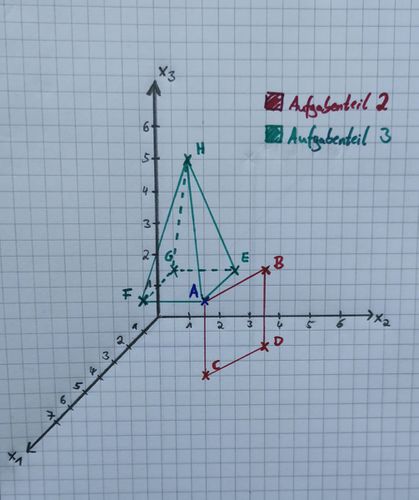
| | {{Box|1= Aufgabe 2: Geometrische Objekte im Koordinatensystem|2= Die abgebildete Pyramide besitzt einen Eckpunkt im Nullpunkt <math> A(0|0|0)</math>. Die quadratische Grundfläche der Pyramide liegt dabei in der <math> x_1</math>-<math> x_2</math>-Ebene und die Spitze der Pyramide liegt 6 Längeneinheiten über der Grundfläche. |
|
| |
|
| | [[Datei:Pyramide.jpg|rahmenlos|500x500px|Pyramide]] |
|
| |
|
|
| |
|
| | <quiz display="simple"> |
| | {Welche Aussage stimmt für die Koordinaten der Punkte <math> B </math>,<math> C </math> und <math> D </math> ?} |
| | - <math> B (5|0|0),C(0|0|5),D(0|5|0) </math> |
| | - <math> B(0|5|0),C(0|5|5),D(0|0|5) </math> |
| | + <math> B (5|0|0),C(5|5|0),D(0|5|0) </math> |
| | - <math> B (1|0|0),C(0|1|1),D(0|0|1) </math> |
| | </quiz> |
|
| |
|
| | <quiz display="simple"> |
| | {Welche Aussage stimmt für den Flächeninhalt der Grundfläche der Pyramide ?} |
| | - Der Flächeninhalt der Grundfläche der Pyramide beträgt <math>5 \text{ LE}^2 </math>. |
| | - Der Flächeninhalt der Grundfläche der Pyramide beträgt <math>10 \text{ LE}^2 </math>. |
| | + Der Flächeninhalt der Grundfläche der Pyramide beträgt <math>25 \text{ LE}^2 </math>. |
| | </quiz> |
| | {{Lösung versteckt|1=Die Gundfläche ist ein Quadrat. Durch Multiplizieren der Längen der Grundflächenkanten erhältst du den Flächeninhalt.|2= Tipp 2|3=Einklappen}} |
|
| |
|
| | <quiz display="simple"> |
| | {Wo liegt der Spitze der Pyramide ?} |
| | + Die Spitze der Pyramide liegt bei <math> S (2{,}5|2{,}5|6) </math>. |
| | - Die Spitze der Pyramide liegt bei <math> S (5|5|5) </math>. |
| | - Die Spitze der Pyramide liegt bei <math> S (2{,}5|2{,}5|5) </math>. |
| | </quiz> |
| | {{Lösung versteckt|1=Die Spitze einer Pyramide liegt mittig über der Grundseite.|2= Tipp 3|3=Einklappen}} |
| | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} |
|
| |
|
| [[Datei:Quader quadratische Grundfläche.png|mini|116x116px]]
| | ==Vektoren als Verschiebungen== |
| Der '''Quader''' besteht aus sechs rechteckigen Seitenflächen, die im rechten Winkel aufeinander stehen. Die gegenüberliegenden Seiten sind jeweils parallel und gleich groß.<br />
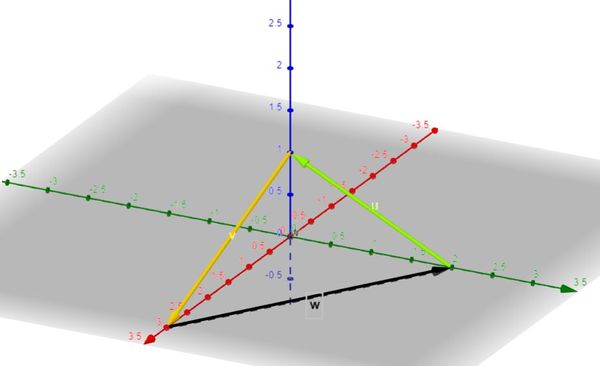
| | {{Box|1= Aufgabe 3: Verschiebungen durch Vektoren|2= Betrachte die dargestellten Verschiebungen <math>\vec{u} </math> (grün) , <math>\vec{v}</math> (gelb) und <math>\vec{w}</math> (schwarz). Außerdem sind die Punkte <math> A(3|0|0)</math>, <math> B(0|2|0)</math> und <math> C(0|0|1)</math> bekannt. |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| |2=Infobox|3=Einklappen}}|
| |
| Merksatz}}
| |
| | |
| | |
| | |
| | |
| | |
| <nowiki>{{Box|1 = Übung 1: Lückentext Körper|2= Ziehe die korrekten Wörter in die jeweiligen Lücken.</nowiki><br /><div class="lueckentext-quiz">
| |
| Im '''Schrägbild''' nimmt man Körper auf der ebenen Fläche '''räumlich''' wahr.
| |
| | |
| Die '''Vorderseite''' des Quaders solltest du in '''Originalgröße''' zeichnen. Wenn der Quader eine '''Länge''' von 8 cm und eine Höhe von 2 cm hat, ist das '''Rechteck''', das du als seine Vorderseite zeichnest, 8 cm breit und 2 cm hoch.
| |
| | |
| Ein Würfel hat '''8''' Ecken, '''6''' Flächen und '''12''' Kanten. Außerdem sind alle Kanten '''gleich''' lang und alle Flächen '''quadratisch'''. Auch sind die Flächen '''gleich''' groß.
| |
| | |
| Eine Pyramide ist ein Körper, der aus einem Vieleck (Drei-, Vier-, Fünfeck usw.) und mehreren '''Dreiecken''' besteht. Das Vieleck bildet die '''Grundfläche''' und die Dreiecke die '''Mantelfläche''' der Pyramide.
| |
| </div> {{Lösung versteckt|1= Schau dir die Infobox zu den bekannten Körpern noch einmal an.|minialternativtext=|2=Tipp|3=Einklappen}}|Farbe={{Farbe|orange}}<nowiki>|3= Arbeitsmethode}}</nowiki> | |
| | |
| | |
| <nowiki>{{Box|Übung 2: Punkte im Koordinatensystem|An welchen Koordinaten liegen die Ecken des angegebenen Tetraeders? </nowiki> | |
| | |
| {{LearningApp|width=100%|height=500px|app=2531036}}
| |
| | |
| {{Lösung versteckt|1= Lies die Aufgabenstellung der App um die Höhe|minialternativtext=|2=Tipp|3=Einklappen}}
| |
| | |
| | |
| <br /> | |
| | |
| ==Schrägbilder und Netze==
| |
| | |
| {{Box|Erinnerung: Schrägbilder und Körpernetze|{{Lösung versteckt|1= Körpernetze und Schrägbilder sind Darstellungshilfen, die man in der Geometrie benutzt. Durch ein Schrägbild wird auf einer ebenen Fläche ein Körper räumlich dargestellt. Beispielsweise kann man einen dreidimensionalen Körper auf einem zweidimensionalen Blatt Papier abbilden.
| |
| *Ein Körpernetz entsteht, wenn man den dreidimensionalen Körper an einigen Kanten aufschneiden und dann auseinanderklappen würde.
| |
| *Bei einem Schrägbild zeichnest du den Köper, wie der Name schon sagt, schräg von der Seite. Hierbei ist wichtig, dass die schrägen Linien meistens im Winkel von <math>45</math>° gezeichnet werden. Je nach Blickpunkt, verändert sich die Perspektive auf den Körper. Die verdeckten Linien, die man von vorne nicht sehen kann, werden gestrichelt dargestellt.|2=Infobox|3=Einklappen}}
| |
| | | |
| Merksatz}}
| |
| | |
| {{Box|Erinnerung: Wie zeichnet man ein Schrägbild?|{{Lösung versteckt|1= Jeder Körper hat eine Grundfläche. Zum Zeichnen von Schrägbildern sollten mehrere Regeln berücksichtigt werden. Zunächst wird die Grundfläche des Körpers in der angegebenen Längeneinheit auf ein Blatt Papier übertragen. Die Längen, die in die Blattebene hinlaufen, werden verkürzt darstellt. Um die Längen zu verkürzen, multipliziert man die reale Länge der Kante mit einem Verkürzungsfaktor <math>q</math>. Der Verkürzungsfaktor <math>q</math> beträgt meistens <math>q= 0{,}5</math>. Zu beachten ist außerdem, dass die verkürzten Kanten schräg gezeichnet werden. Die Höhe steht immer senkrecht auf der Grundfläche und wird in der angegebenen Längeneinheit gezeichnet.|2=Infobox|3=Einklappen}}
| |
| | |
| Beispielkonstruktion eines Quaders:
| |
| <ggb_applet id="SQm8Xq3y" width="1009" height="483" border="888888" sdz="true" /><br />
| |
| |Merksatz}}<br />
| |
| ==='''Übungen: Netze'''===
| |
| | |
| {{Box|1= Übung 1: Würfelnetze|2= Giovanni, Yasmin und Mehmet haben jeweils das Netz eines Würfels gezeichnet. Beurteile, ob die Körpernetze korrekt gezeichnet wurden.[[Datei:Lösung Würfelnetze.jpg|mini | alternativtext=|zentriert|500x500px]] {{Lösung versteckt|1=Stelle dir vor, dass du die Kanten aneinander klebst. Was kannst du ausschließen? Welche Eigenschaften kennst du, die hier nicht zutreffen?|2= Tipp|3=Einklappen}}Wer hat richtig gezeichnet?
| |
| <div class="multiplechoice-quiz"> | |
| (Giovanni und Yasmin) (!Alle) (!Yasmin und Mehmet) (!Giovanni und Mehmet) | |
| </div>|Farbe={{Farbe|orange}}|3= Arbeitsmethode}}
| |
| | |
| | |
| | |
| <br />{{Box|Übung 2: Kanten kleben|Markiere die Kanten, die die gleiche Kantenlänge haben, in derselben Farbe!<ggb_applet id="dugsrtcf" width="1000" height="800" border="888888" sdz="true" />{{Lösung versteckt|1= Stell dir am Besten vor, wie du die Seiten des Netzes knicken und verkleben musst, damit der Körper eines Prismas entsteht.
| |
| |2=Tipp|3=Einklappen}}|Arbeitsmethode
| |
| | Farbe={{Farbe|orange}} }}
| |
| | |
| | |
| {{Box|1= Übung 3: Wahr- und Falschaussagen über Schrägbilder|2= Bestimme, ob die folgenden Aussagen wahr oder falsch sind.
| |
| <div class="multiplechoice-quiz">
| |
| | |
| Wenn ein Quader im Schrägbild dargestellt wird, dann sind die Deck- und die Grundfläche immer gleich groß. (wahr) (!falsch)
| |
| | |
| Es gibt mehr als eine Lösung für Körpernetze von Schrägbildern. (wahr) (!falsch)
| |
| | |
| Schrägbilder haben keine versteckten Ecken oder Kanten. (wahr) (!falsch)
| |
| | |
| Schrägbilder stellen geometrische Figuren auf dem Papier dar. (wahr) (!falsch)
| |
| </div> | |
| | |
| Falls ihr eine Frage falsch beantwortet habt, könnt ihr hier noch einmal die Erklärung zu den Lösungen nachgucken.
| |
| {{Lösung versteckt|1=1) Bei der Konstruktion eines Quaders werden lediglich die nach hinten verlaufenden Kanten verkürzt dargestellt. Da Deck- und Grundfläche parallel zueinander liegen, sind sie immer gleichgroß.
| |
|
| |
| 2) Zu jedem Körper gibt es mehrere Netze. Je nach dem welche Kante aufgeschnitten wird, entsteht ein anderes Netz.
| |
| | |
| 3) Wenn du das Schrägbild korrekt gezeichnet hast, dann solltest du aus verschiedenen Perspektiven immer alle Ecken und Kanten sehen können.
| |
|
| |
|
| 4) Du konstruierst Schrägbilder, um geometrische Figuren bzw. räumliche Körper auf dem Papier darzustellen.|2=Erklärungen|3=Einklappen|Farbe={{Farbe|orange}}}}|Farbe={{Farbe|orange}}|3= Arbeitsmethode}}
| | [[Datei:Vektoren.jpg|rahmenlos|600x600px]] |
|
| |
|
| | Welche Punkte erhältst du bei folgenden Verschiebungen durch die Vektoren? |
|
| |
|
| {{Box|Übung 4: Netze der bekannten Körper| | | # <math> A(3|0|0)</math> <math>+ \vec{w} </math> |
| Für die folgende Aufgabe benötigst du einen gespitzten Bleistift, dein Heft und Geodreieck. Zeichne das Netz
| | # <math> C(0|0|1)</math> <math> - \vec{u} </math> |
| | # <math> A(3|0|0)</math> <math> - \vec{u}-\vec{w}-\vec{v} </math> |
| | # <math> C(0|0|1) </math> <math>- \vec{u}+\vec{u}</math> |
| | # <math> B(0|2|0) </math> <math> + 2 \cdot \vec{u} + 2 \cdot \vec{v} + \vec{w} </math> |
|
| |
|
| '''a)''' einer Pyramide, welche aus vier gleichseitigen Dreiecken mit Seitenlänge <math>2</math> cm und einer quadratischen Grundfläche mit Seitenlänge von <math>2</math> cm besteht.
| |
| {{Lösung versteckt|1= Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.|2= Tipp zu a)|3=Einklappen}}
| |
| {{Lösung versteckt|1=[[Datei:Pyramidennetz a.jpg|mini]]|2= Lösung|3=Einklappen}}
| |
| '''b)''' eines Tetraeder mit Seitenlänge <math>2</math> cm.
| |
| {{Lösung versteckt|1=Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.|2= Tipp zu b)|3=Einklappen}}
| |
| {{Lösung versteckt|1=[[Datei:Tetraedernetz b.jpg|mini]]|2= Lösung|3=Einklappen}}
| |
| '''c)''' eines Quaders, welcher <math>1</math> cm breit, <math>2</math> cm lang und <math>1</math> cm hoch ist.
| |
| {{Lösung versteckt|1= Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.|2= Tipp zu c)|3=Einklappen}}
| |
| {{Lösung versteckt|1=[[Datei:Quadernetz.jpg|mini]]|2= Lösung|3=Einklappen}}
| |
| '''d)''' eines dreieckigen Prismas, welches aus zwei gleichseitigen Dreiecken mit Seitenlänge <math>1</math> cm besteht. Die Breite des Prismas soll <math>2</math> cm betragen.{{Lösung versteckt|1=Beachte die Infobox zu Netzen. Wenn dir das nicht weiter hilft, scrolle ans Ende der Seite.|2= Tipp zu d)|3=Einklappen}} {{Lösung versteckt|1=[[Datei:Prismanetz d.jpg|mini|216x216px]]|2= Lösung|3=Einklappen}}
| |
| |Arbeitsmethode}}
| |
|
| |
|
|
| |
|
| |
|
| |
| {{Box|1= Übung 5: Netze zusammenfalten|2= Sind die gegebenen Netze die Netze einer Pyramide? Die weiteren Netze erscheinen, wenn du den Regler auf der rechten Seite bewegst. <ggb_applet id="abxbyZSC" width="1062" height="524" border="888888" />
| |
|
| |
| <div class="multiplechoice-quiz">
| |
|
| |
| Netz 1 ist das Netz einer Pyramide. (wahr) (!falsch)
| |
|
| |
| Netz 2 ist das Netz einer Pyramide. (!wahr) (falsch)
| |
|
| |
| Netz 3 ist das Netz einer Pyramide. (wahr) (!falsch)
| |
|
| |
| Netz 4 ist das Netz einer Pyramide. (!wahr) (falsch)
| |
|
| |
| Netz 5 ist das Netz einer Pyramide. (!wahr) (falsch)
| |
| </div>
| |
| {{Lösung versteckt|1= | | {{Lösung versteckt|1= |
| *Netz 1 ist das Netz einer Pyramide, da alle Seiten der Dreiecke sich treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils gleich lang sind.
| | # <math> B(0|2|0)</math> |
| *Netz 2 ist nicht das Netz einer Pyramide, da die längeren Seiten des höheren Dreiecks nicht mit den des weniger hohen Dreiecks übereinstimmen.
| | # <math> B(0|2|0)</math> |
| *Netz 3 ist das Netz einer Pyramide, da alle Seiten der Dreiecke sich treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils gleich lang sind.
| | # <math> A(3|0|0)</math> |
| *Netz 4 ist nicht das Netz einer Pyramide, da die Seiten der Dreiecke sich nicht treffen, wenn man die Dreiecke nach unten versucht zusammenzuklappen, d.h. die benachbarten Seiten der Dreiecke sind jeweils nicht gleich lang.
| | # <math> C(0|0|1)</math> |
| *Netz 5 ist nicht das Netz einer Pyramide, da die Seiten der Dreiecke sich nicht treffen, d.h. dass die benachbarten Seiten der Dreiecke jeweils nicht gleich lang sind.
| | # <math> A(3|0|0)</math> |
| |alternativtext=|2=Lösung|3=Einklappen}}|3= Arbeitsmethode}}
| | |2= Lösung|3=Einklappen}} |
|
| |
|
| | |Farbe={{Farbe|orange}}|3= Arbeitsmethode}} |
|
| |
|
| {{Box|Übung 6: Netze von Prismen|Zeichne die folgenden Netze in dein Heft und ergänze fehlende Flächen, damit das Netz eines Prismas entsteht.[[Datei:Angefangene Netze eines Prismas.jpg|mini|alternativtext=|zentriert]] | | ==Rechnen mit Vektoren== |
| | {{Box|1= Aufgabe 4: Vektoren addieren und mit einem Skalar multiplizieren|2= |
|
| |
|
| {{Lösung versteckt|1= Schau dir zunächst noch einmal an, wie ein Prisma aussieht und welche Flächen es hat. Dann überlege dir, welche Flächen in den gegebenen Netzen fehlen könnten. | | {{LearningApp|width=100%|height=500px|app=11071387}} |
| |2=Tipp|3=Einklappen}} | |
| {{Lösung versteckt|1= Vergleiche die angegebenen Lösungen mit deinen eigenen Netzen. Bei dieser Aufgabe solltest du beachten, dass die angegebenen Lösungen nur mögliche Lösungen sind. [[Datei:Aufgabe Prisma Lösung.jpg|mini|alternativtext=|zentriert]] |2=Lösung|3=Einklappen}}|Arbeitsmethode|Farbe={{Farbe|orange}}}}
| |
| <br />
| |
|
| |
|
| | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} |
|
| |
|
| ==='''Übungen: Schrägbilder'''===
| | {{Box|1= Aufgabe 5: Lückentext - Geometrische Bedeutung von Vektoraddition und skalarer Multiplikation|2= |
| | |
| <br />
| |
| | |
| {{Box|1=Übung 1: Memory|2=Gegeben sind Körpernetze und Schrägbilder. Finde die passenden Paare. | |
| | |
| <div class="memo-quiz">
| |
|
| |
| | |
| {{{!}}
| |
| | |
| {{!}}[[File:Square pyramid.png|thumb|Quadratische Pyramide|alternativtext=|125x125px]]{{!}}{{!}}[[Datei:Pyramide Netz 2.png|mini|alternativtext=|125x125px]]
| |
| | |
| {{!}}-
| |
| | |
| {{!}}[[File:120px-Hexahedron-slowturn.gif|thumb|120px-Hexahedron-slowturn|alt=120px-Hexahedron-slowturn.gif]]{{!}}{{!}}[[File:Hexahedron flat color.svg|thumb|Hexahedron flat color|alt=Hexahedron flat color.svg|144x144px]]
| |
| | |
| {{!}}-
| |
| | |
| {{!}}[[File:120px-Tetrahedron-slowturn.gif|thumb|120px-Tetrahedron-slowturn|alt=120px-Tetrahedron-slowturn.gif]]{{!}}{{!}}[[File:Tetrahedron flat.svg|thumb|Tetrahedron flat|alternativtext=|110x110px]]
| |
| | |
| {{!}}-
| |
| | |
| {{!}}[[File:Cuboid abcd.svg|thumb|Quader mit Raumdiagonale d|alternativtext=|125x125px]]{{!}}{{!}}[[File:QuaderNetz.svg|thumb|Auseinander geklapptes Netz eines Quaders|alternativtext=|131x131px]]
| |
| | |
| {{!}}-
| |
| | |
| {{!}}[[File:Triangular prism.svg|thumb|dreieckiges Prisma|alternativtext=|143x143px]]{{!}}{{!}}[[Datei:Desarrollo prisma triangular.png|mini|alternativtext=|125x125px]]
| |
| | |
| {{!}}}
| |
|
| |
|
| | <div class="lueckentext-quiz"> |
| | Wir definieren zwei '''Rechenoperationen''' für Vektoren: das Bilden des Vielfachen und der Summe. Die '''Vektoraddition''' bezeichnet das Bilden der '''Summe''' zweier Vektoren gleichen Typs. Gleichen Typs heißt, dass die beiden Vektoren gleich viele '''Komponenten''' haben. Man bildet die Summe, indem man die '''Komponenten''' der Vektoren '''komponentenweise''' addiert. Wir können uns die Addition von Vektoren als ein „'''Aneinanderlegen'''“ von zwei '''Pfeilen''' von ggf. verschiedener Länge vorstellen. Wenn wir <math> \vec{a} </math> und <math> \vec{b}</math> als '''Pfeile''' deuten, bedeutet die Addition, dass wir die '''Pfeile''' hintereinanderlegen, so dass der '''Anfang''' von <math> \vec{b} </math> und die „'''Spitze'''“ von <math> \vec{a} </math> übereinstimmen. Eine derartige Verwendung von Pfeilen ist aus der '''Physik''' bekannt. Dort werden oftmals '''Kräfte''' und Geschwindigkeiten mit Pfeilen dargestellt. Man kann am Ende zur Addition sagen, dass das Bilden der Summe zweier Vektoren <math> \vec{a} + \vec{b} </math> als '''Hintereinander-Ausführen''' der durch <math> \vec{a} </math> und <math> \vec{b} </math> dargestellten '''Verschiebungen''' gesehen werden kann. |
| </div> | | </div> |
|
| |
|
| {{Lösung versteckt|1= * Falls du nicht mehr weißt, wie die Schrägbilder der bekannten Körper aussehen, dann guck noch einmal in der Erinnerungsbox zu den bekannten Körpern nach.
| | <div class="lueckentext-quiz"> |
| * Falls du nicht mehr weißt, wie die Netze der bekannten Körper aussehen, dann guck noch einmal hier nach: Das Netz eines Quaders, dreieckigen Prismas, einer Pyramide und eines Tetraeders findest du in den Lösungen von Aufgabe "nach Konstruktion zeichnen". Das Netz eines Würfels siehst du, wenn du Aufgabe 1 zu Schrägbildern richtig gelöst hast.
| | Das Bilden des '''Vielfachen''' eines Vektors wird auch als '''Multiplikation mit einem Skalar''' bezeichnet. Wir nennen unseren '''Vektor''' wieder <math> \vec{a} </math> und das '''Skalar''' bezeichnen wir mit <math> c </math>. Von jedem Vektor kann das '''<math> c </math> -Fache''' gebildet werden, indem '''alle Komponenten''' von <math> \vec{a} </math> '''mit <math> c </math> multipliziert''' werden. Ist '''<math> c>0 </math>''' so wird der „Pfeil“ von <math> \vec{a} </math> um den Faktor <math> c </math> gestreckt ('''falls <math>c > 1</math>''') oder gestaucht ('''falls <math>c < 1</math> '''). Ist '''<math>c<0</math>''', so erhält der Pfeil, der um den Faktor <math> c </math> gestreckt oder getaucht wird, noch eine '''Richtungsumkehrung'''. Für den Fall ''' <math> c=-1 </math> ''' sprechen wir dann vom '''Gegenvektor''' von <math> \vec{a} </math>. |
| |2=Tipp |3=Einklappen}}
| |
| |3=Arbeitsmethode|Farbe={{Farbe|orange}}
| |
| }}
| |
| | |
| | |
| {{Box|Übung 2: Schrägbild zeichnen|Wie sieht das Schrägbild des folgenden Körpernetzes aus? Zeichne die Lösung in dein Heft und überprüfe dein Ergebnis mit der angegebenen Lösung.[[Datei:Körpernetz Quader.jpg|mini|alternativtext=|zentriert]]
| |
| | |
| {{Lösung versteckt|1= Falls du keine Idee hast, um welchen Körper es sich hier handeln könnte, schau dir oben noch einmal die Erinnerung der bekannten Körper an.
| |
| |2=Tipp 1|3=Einklappen}}
| |
| | |
| {{Lösung versteckt|1= Wenn du das Netz einem Körper zu ordnen konntest, dann überlege dir welche Seiten zu einander parallel sind.
| |
| |2=Tipp 2|3=Einklappen}}
| |
| | |
| {{Lösung versteckt|1= Das angegebene Netz ist das Netz eines Quaders. Jetzt solltest du es mit den angegebenen Längeneinheiten zeichnen können.
| |
| |2=Tipp 3|3=Einklappen}}
| |
| | |
| {{Lösung versteckt|1= Vergleiche die angegebene Lösung mit deiner Lösung im Heft. [[Datei:Aufgabe Lösung.jpg|mini|alternativtext=|zentriert]] |2=Lösung|3=Einklappen}}|Arbeitsmethode| }}
| |
| | |
| | |
| {{Box|Übung 3: Zeichnung eines Netzes|Zeichne das Netz des folgenden Schrägbildes und benutze die angegebenen Längen. Zeichne das Netz in dein Heft.[[Datei:Schrägbild Trapezprisma.jpg|zentriert|mini]]
| |
| {{Lösung versteckt|Fange mit der größten quadratischen Grundfläche an, und überlege, wie du von hieraus ein Netz formen kannst.|2=Tipp 1|3=Einklappen}}
| |
| {{Lösung versteckt|Welche Kanten des Körper musst du ,,einschneiden" um das Netz zu formen? Überlege dir, was passiert, wenn du einige Kanten ,,einschneidest". Entsteht so dein Körpernetz?|2=Tipp 2|3=Einklappen}}
| |
| {{Lösung versteckt|,,Schneide" alle Kanten ein, die senkrecht von der quadratischen Grundfläche hochführen. Trenne nun die nicht-rechteckigen Seitenflächen der Grundfläche von der gegenüberliegenden Fläche der Grundfläche. Nun muss nur noch eine Kante ,,eingeschnitten" werden, um das Körpernetz zu erhalten.|2=Tipp 3|3=Einklappen}} {{Lösung versteckt|[[Datei:Netz Trapezprisma.jpg|zentriert|mini]] So sieht eine mögliche Lösung des Körpernetztes des gegebenen Schrägbildes aus. Die Seiten, die senkrecht der Grundfläche hochgehen, wurden ,,eingeschnitten". Danach wurden die anliegenden nicht-rechteckigen Seiten der Grundfläche von der gegenüberliegenden Fläche der Grundfläche getrennt. Als letztes wurde eine rechteckige Seitenfläche der Grundfläche von der gegenüberliegenden Fläche der Grundfläche getrennt.|2=Lösung|3=Einklappen}}
| |
| |Arbeitsmethode| Farbe={{Farbe|grün|dunkel}}}}
| |
| | |
| | |
| | |
| | |
| {{Box|Übung 4: Schrägbilder korrigieren| Sofia hat im Unterricht das Schrägbild eines dreieckigen Prismas und eines Quaders, sowie Schrägbilder zweier Pyramiden gezeichnet. Beurteile, ob die Schrägbilder richtig sind. Falls sie falsch sind, finde die Fehler und korrigiere die Schrägbilder.[[Datei:Falsche Figuren.jpg|mini|alternativtext=|zentriert|300x300px]]
| |
| {{Lösung versteckt|*[[Datei:Fehler Pyramide.jpg|mini]] Figur 1: Die versteckten Linien wurden nicht gestrichelt gezeichnet.
| |
| *[[Datei:Fehler Quader.jpg|mini]] Figur 2: Hier liegt der Fehler darin, dass die markierten Längen, die in die Blattebene hinlaufen, auf der linken Seite des Quaders nicht denselben Winkel haben wie die anderen beiden, die in die Blattebene laufen, auf der rechten Seite. (Hier hättest du genauso gut die anderen beiden Längen, die in Blattebene hineinlaufen, auf der rechten Seite als Fehler markieren können.) Weiterhin wurde die hintere versteckte Linien nicht gestrichelt gezeichnet.
| |
| *[[Datei:Fehler Prisma.jpg|mini]] Figur 3: Hier sehen wir, dass die markierte Länge, die in die Blattebene hinlaufen, nicht denselben Winkel haben wie die anderen beiden, die in die Blattebene laufen. Somit verändert sich auch die eine Seite des hinteren Dreiecks.
| |
| * Figur 4 wurde richtig gezeichnet.
| |
| |2=Fehler|3=Einklappen}}
| |
| {{Lösung versteckt|[[Datei:Korrektur1.jpg|mini]]|2=Korrektur|3=Einklappen}}|Arbeitsmethode|}}
| |
| | |
| | |
| {{Box|
| |
| 1= Übung 5: Zeichnen und Messen - Quader|
| |
| 2= Ein Quader hat eine Länge von <math>8</math> cm, eine Breite von <math>8</math> cm und eine Höhe von <math>4</math> cm. Zeichne sein Schrägbild in dein Heft und miss mit dem Lineal nach, wie weit die Ecke unten links vorn von der Ecke oben rechts hinten entfernt ist.
| |
| | |
| | |
| | |
| <div class="multiplechoice-quiz"> | |
| Die gesuchte Strecke ist
| |
| (<math>12{,}8</math> cm lang.) (!<math>10{,}1</math> cm lang.) (!<math>14{,}3</math> cm lang.) (!<math>8{,}6</math> cm lang.)
| |
| </div>
| |
| | |
| {{Lösung versteckt|1= Zunächst zeichnest du in wahrer Länge die Vorderseite des Quaders. Das Rechteck hat dann eine Länge von <math>8</math> cm und eine Höhe von <math>4</math> cm.
| |
| |2=Tipp 1|3=Einklappen}}
| |
| {{Lösung versteckt|1= Im zweiten Schritt zeichnest du von den vier Eckpunkten jeweils eine Hilfsgerade im Neigungswinkel <math>45</math>°.
| |
| |2=Tipp 2|3=Einklappen}}
| |
| {{Lösung versteckt|1= Jetzt multiplizierst du die angegebene Breite mit dem Verkürzungsfaktor <math>q = 0{,}5</math>. Die errechnete Kantenlänge von <math>4</math> cm soll jetzt die Länge der Hilfsgeraden darstellen. Hier passt du deine anfänglich gezeichneten Hilfsgeraden an die Länge von <math>4</math> cm an.
| |
| |2=Tipp 3|3=Einklappen}}
| |
| {{Lösung versteckt|1= Die neu konstruierten Punkte verbindest du abschließend noch miteinander und zeichnest die nicht sichtbaren Linien gestrichelt ein. |2=Tipp 4 |3=Einklappen}} | |
| {{Lösung versteckt|1= Die gesuchte Strecke beträgt <math>12{,}8</math> cm.[[Datei:Lösungsskizze.jpg|mini|alternativtext=|zentriert]] |2=Lösung|3=Einklappen}}|Farbe={{Farbe|orange}}|3= Arbeitsmethode}}
| |
| | |
| | |
| {{Box|1= Übung 6: Zeichnen und Messen - Prisma| 2= Ein gleichseitiges Prisma hat eine Seitenlänge von <math>a=6</math> cm und eine Höhe von <math>h=5</math> cm. Zeichne das Schrägbild in dein Heft und miss mit dem Lineal nach, wie weit die vordere Ecke unten rechts von der hinteren Ecke oben entfernt ist.
| |
| <div class="multiplechoice-quiz">
| |
| Die gesuchte Strecke ist
| |
| (<math>6{,}9</math> cm lang.) (!<math>5{,}3</math> cm lang.) (!<math>7{,}4</math> cm lang.) (!<math>5{,}8</math> cm lang.)
| |
| </div>
| |
| {{Lösung versteckt|1= Zunächst zeichnest du die Strecke <math>AB=6</math> cm in wahrer Länge.
| |
| |2=Tipp 1|3=Einklappen}}
| |
| {{Lösung versteckt|1= Da es sich bei dem Körper um ein gleichseitiges Prisma handelt, schneidet die Höhe die Strecke <math>AB</math> genau im Mittelpunkt <math>P</math>. Von diesem Punkt <math>P</math> ziehst du nun in einem Winkel von <math>45</math>° eine Hilfslinie. Um die Länge der Hilfslinie zu ermitteln, multiplizierst du die angegebene Höhe mit <math>0{,}5</math> . Hier hätte die Strecke dann eine Länge von <math>2{,}5</math> cm.
| |
| |2=Tipp 2|3=Einklappen}}
| |
| {{Lösung versteckt|1= Jetzt verbindest du den entstandenen Punkt <math>C</math> mit den Punkten <math>A</math> und <math>B</math>, um die Grundfläche des Prismas zu erhalten.
| |
| |2=Tipp 3|3=Einklappen}}
| |
| {{Lösung versteckt|1= Nun zeichnest du jeweils von den Punkten <math>A, B</math>, und <math>C</math> eine senkrechte Linie, die der Höhe von <math>5</math> cm entspricht. Um die Konstruktion abzuschließen, verbindest du die weiteren Eckpunkte miteinander.|2=Tipp 4 |3=Einklappen}}
| |
| | |
| | |
| {{Lösung versteckt|1= Die gesuchte Strecke beträgt <math>6{,}9</math> cm.[[Datei:Aufgabe Lösung Prisma.jpg|mini|alternativtext=|zentriert]]|2=Lösung|3=Einklappen}} |3= Arbeitsmethode}}
| |
| | |
| | |
| {{Box|Übung 7: nach Konstruktionsbeschreibung zeichnen|Für diese Aufgabe benötigst du einen gespitzten Bleistift, Heft und Geodreieck. Zeichne eine Pyramide mithilfe folgender Konstruktionsbeschreibung. Die Kantenlängen kannst du frei wählen.
| |
| | |
| ''Schritt 1:'' Die quadratische Grundfläche der Pyramide wird als Parallelogramm <math>ABCD</math> gezeichnet. Dabei werden die nach hinten verlaufenden Kanten im Winkel von <math>45</math>° gezeichnet und in ihrer Länge halbiert. | |
| | |
| ''Schritt 2:'' Die Spitze <math>S</math> der Pyramide wird senkrecht über dem Mittelpunkt der Grundfläche <math>ABCD</math> angenommen. | |
| | |
| ''Schritt 3:'' Die Spitze <math>S</math> der Pyramide wird mit den Eckpunkten <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> der Grundfläche verbunden. Sichtbare Linien werden durchgezeichnet. Nicht sichtbare Linien werden punktiert. | |
| {{Lösung versteckt|1= Weil die Lösung nicht in dieser Box angezeigt werden kann, scrolle ganz ans Ende der Seite, um die Lösung zu sehen.|2=Lösung|3=Einklappen}}|Arbeitsmethode}}
| |
| | |
| | |
| ==Unmögliche Figuren==
| |
| | |
| {{Box|Unmögliche Figuren|Falls du dir unsicher bist, was unmögliche Figuren sind, lies dir die Infobox einmal durch.{{Lösung versteckt|1= '''Unmögliche Figuren''' sind grafisch zweidimensionale Figuren, die dreidimensional erscheinen aber als Körper in der Realität nicht existieren können. Die geometrischen, dreidimensionalen Objekte kann man in der Realität gar nicht herstellen. Gezeichnet werden können sie auf (dem zweidimensionalen) Papier aber ohne Probleme. Bei den Figuren handelt es sich meist um optische Täuschungen.|2=Infobox|3=Einklappen}}'''<big>Beispiele von unmöglichen Figuren:</big>'''
| |
| | |
| | |
| {{2Spalten
| |
| |[[Datei:Lattenkiste_a.jpg|alternativtext=|ohne|mini|193x193px|Die unmögliche Lattenkiste]]
| |
| |[[Datei:Impossible_cube_illusion_angle.svg|alternativtext=|mini|Unmöglicher Würfel|ohne|199x199px]]
| |
| }}|
| |
| Merksatz}}
| |
| | |
| | |
| {{Box|Idee| 2 = Vielleicht kennst du ja auch schon ein paar unmögliche Figuren, natürlich nicht aus unserer Realität, aber ja aus Filmen? Eine der obigen Figuren kommt zum Beispiel in einer Szene aus ''Inception'' (2010) vor, die du dir hier auf YouTube angucken kannst:{{#ev:youtube|dvSD1EAlAUQ}}|3 = Hervorhebung1| Farbe={{Farbe|gelb}}}}
| |
| | |
| | |
| ===Übungen: unmögliche Figuren===
| |
| | |
| {{Box|1=Übung 1: Erkennst du die unmöglichen Figuren? |2=Im unteren Kasten siehst du unmögliche Figuren und nicht unmögliche Figuren. Bestimme, ob die Figuren unmöglich sind oder nicht. Ziehe dafür das Bild in den zugehörigen Kasten.
| |
| | |
| <div class="zuordnungs-quiz"> | |
|
| |
| | |
| {{{!}} | |
| | |
| {{!}}unmögliche Figuren {{!}}{{!}} [[File:Impossible cube illusion angle.svg|thumb|alternativtext=|154x154px]] {{!}}{{!}} [[File:Reutersvärd’s triangle.svg|thumb|alternativtext=|150x150px]]{{!}}{{!}}[[File:Blivet.png|thumb|alternativtext=|200x200px]]{{!}}{{!}}[[File:Impossible staircase.svg|thumb|alternativtext=|200x200px]]
| |
| | |
| {{!}}-
| |
| | |
| {{!}}geometrische Körper/Konstruktionen{{!}}{{!}} [[Datei:Cube-2351867 640.jpg|mini|alternativtext=|200x200px]] {{!}}{{!}} [[File:Deutsches Technikmuseum Berlin February 2008 0005.JPG|thumb|alternativtext=|200x200px]] {{!}}{{!}} [[Datei:Treppe-zp-beisp1.svg|mini|167x167px]]
| |
| | |
| {{!}}}
| |
|
| |
| | |
| </div> | |
|
| |
|
| | Wir nennen zwei Vektoren '''kollinear''' (oder parallel), wenn einer der Vektoren ein '''Vielfaches des anderen''' ist. Mit anderen Worten: Wenn <math> \vec{a} </math> und <math> \vec{b} </math> zwei '''verschiedene''' Vektoren sind, so sind sie '''parallel/kollinear''' zueinander, falls ein '''Skalar <math> c </math>''' existiert, sodass gilt: '''<math> c \vec{a}=\vec{b} </math>'''. Dabei ist es egal, ob die beiden Vektoren in '''verschiedene''' '''Richtungen''' zeigen oder nicht. |
| | </div> |
| |3=Arbeitsmethode}} | | |3=Arbeitsmethode}} |
|
| |
|
| | ==Kollinearität von Vektoren== |
| | {{Box|1= Aufgabe 6: Kollinearität von Vektoren|2= |
|
| |
|
| <br />
| | {{LearningApp|width=100%|height=500px|app=11504986}} |
| | |
| | |
| {{Box|Übung 2: Aus unmöglich mach möglich!|Wie müsste man den unmöglichen Würfel verändern, damit diese/r keine unmögliche Figur mehr ist? [[Datei:Impossible_cube_illusion_angle.svg|alternativtext=|mini|Unmöglicher Würfel|ohne|199x199px]]{{Lösung versteckt|1= Man müsste die hinteren Seitenkannten des Würfels zerschneiden, um die vorderen an dieser Stelle sichtbar zu machen. Einen echten, nicht unmöglichen Würfel siehst du hier: | |
| [[Datei:Cube-2351867 640.jpg|mini|alternativtext=|zentriert]]|2=Lösung|3=Einklappen}}
| |
| |Arbeitsmethode| Farbe={{Farbe|grün|dunkel}}}}
| |
| | |
| | |
| {{Box | Übung 3: Das Penrose-Dreieck|Betrachte das sogenannte Penrose-Dreieck. Welche Besonderheiten fallen dir auf? Wordurch wird die optische Täuschung hervorgerufen? Welches mathematische Gesetz zeigt, dass das Dreieck im Dreidimensionalen nicht existieren kann? Beantworte im Heft.[[Datei:Penrose triangle.svg|zentriert|mini]]
| |
| | |
| {{Lösung versteckt|1=In welchem Winkel stehen die Seiten des Dreiecks aufeinander?|2=Tipp 1|3=Einklappen}}
| |
| {{Lösung versteckt|1=Was ist die Winkelsumme eines "möglichen" Dreiecks?|2=Tipp 2|3=Einklappen}}
| |
| {{Lösung versteckt|1=Das Penrose-Dreieck hat drei Seiten, die jeweils im rechten Winkel zueinander stehen und dennoch zu einem Dreieck verbunden sind. Damit verstößt es gegen mehrere mathematische Gesetze der Geometrie. Zum Beispiel beträgt die Winkelsumme in einem Dreieck immer <math>180</math>°.|2=Lösung|3=Einklappen}}|Arbeitsmethode| Farbe={{Farbe|grün|dunkel}}}}
| |
| | |
| | |
| <br />
| |
| | |
| | |
| | |
| | |
| | |
| | |
| ===Quellen===
| |
| {{Lösung versteckt|1= *https://learnattack.de/mathematik/koerpernetz-und-schraegbild-von-koerpern#video-was-sind-schr%C3%A4gbild-und-netz-eines-k%C3%B6rpers
| |
| *https://www.geogebra.org/m/a7wZdw5C#material/Qf9yn4sG
| |
| *https://www.geogebra.org/m/SQm8Xq3y
| |
| *https://www.geogebra.org/m/ab93zf9g
| |
| *https://www.geogebra.org/m/nc7KHTJt
| |
| *https://www.geogebra.org/material/show/id/ab93zf9g#
| |
| *https://www.geogebra.org/material/show/id/Z57aCNpm#
| |
| *https://www.youtube.com/watch?v=dvSD1EAlAUQ
| |
| *https://www.klippert-medien.de/media/ntx/klippert/sample/09108DA5_Musterseite.pdf
| |
| *https://nl.wikipedia.org/wiki/Onmogelijke_figuur#/media/Bestand:Blivet.png
| |
| *https://de.wikipedia.org/wiki/Unm%C3%B6gliche_Figur#/media/Datei:Impossible_staircase.svg
| |
| *https://de.wikipedia.org/wiki/Penrose-Dreieck#/media/Datei:Deutsches_Technikmuseum_Berlin_February_2008_0005.JPG
| |
| *https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Reutersv%C3%A4rd%E2%80%99s_triangle.svg
| |
| *https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Impossible_cube_illusion_angle.svg|2=Orientiert an|3=Einklappen}}
| |
| | |
| | |
| | |
| <br />
| |
| ===Geogebra Applets===
| |
| | |
| ======Pyramidenaufgabe Übung 6 Lösung======
| |
| <ggb_applet id="Z57aCNpm" width="750" height="550" border="888888" />
| |
| ======Netzaufgabe Übung 4 a Tipp======
| |
| <ggb_applet id="Jhc3FeP8" width="750" height="550" border="888888" />
| |
| ======Netzaufgabe Übung 4 b Tipp======
| |
| <ggb_applet id="QU97VcUE" width="950" height="550" border="888888" />
| |
| ======Netzaufgabe Übung 4 c Tipp======
| |
| <ggb_applet id="UaEEaDy7" width="800" height="550" border="888888" />
| |
| ======Netzaufgabe Übung 4 d Tipp======
| |
| <ggb_applet id="EwEjZUYn" width="869" height="486" border="888888" />
| |
|
| |
|
| | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} |
|
| |
|
| ==Aufgabe 8 - Länge und Abstände von Vektoren== | | ==Länge und Abstände von Vektoren== |
| | | {{Box|1=Aufgabe 7: Länge und Abstände von Vektoren|2= |
| {{Box|1=Aufgabe 8 - Länge und Abstände von Vektoren|2= | |
| <quiz display="simple"> | | <quiz display="simple"> |
| {Berechne die Länge der Vektoren:} | | {Berechne die Länge der Vektoren:} |
|
| |
|
| {a) <math> \vec{v} = \begin{pmatrix} 3 \\ -4 \\ 0 \end{pmatrix} </math>} | | { <math> \vec{v} = \begin{pmatrix} 12 \\ 3 \\ 4 \end{pmatrix} </math>} |
| - 4 | | - <math> 11 </math> |
| + 5
| | - <math> 12 </math> |
| - 6 | | + <math> 13 </math> |
| - 7
| | - <math> 14 </math> |
| | |
| {b) <math> \vec{v} = \begin{pmatrix} 12 \\ 3 \\ 4 \end{pmatrix} </math>}
| |
| - 11
| |
| - 12
| |
| + 13 | |
| - 14 | |
|
| |
|
| {c) <math> \vec{v} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} </math>} | | { <math> \vec{v} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix} </math>} |
| - 1 | | - <math> 1 </math> |
| - 2 | | - <math> 2 </math> |
| + <math> \sqrt{2} </math> | | + <math> \sqrt{2} </math> |
| - <math> frac 1 2 </math> | | - <math> \frac{1}{2} </math> |
| </quiz> | | </quiz> |
| | |
| | {{Lösung versteckt|1=Man berechtnet die Länge eines Vektors wie folgt: Man quadriert jede Komponente des Vektors. Anschließend werden diese addiert und zum Schluss wird aus dem Ergebnis die Wurzel gezogen.|2=Tipp 1|3=Tipp verbergen}} |
|
| |
|
| <quiz display="simple"> | | <quiz display="simple"> |
| {Berechne den Abstand der Punkte:} | | {Berechne den Abstand der Punkte:} |
|
| |
|
| {a)<math> A(2|-4|1) </math> und <math> B(4|-4|-2) </math>} | | {<math> A(8|9|10) </math> und <math> B(2|6|8) </math>} |
| + 3
| | - <math> 9{,}5 </math> |
| - 6
| | + <math> 7 </math> |
| - 9 | | - <math> 8 </math> |
| - 12
| | - <math> 6{,}5 </math> |
| | |
| {b)<math> A(8|9|10) </math> und <math> B(2|6|8) </math>}
| |
| - 9,5
| |
| + 7
| |
| - 8 | |
| - 6,5 | |
| </quiz> | |
| |3=Arbeitsmethode|Farbe={{Farbe|gelb|dunkel}}}}
| |
|
| |
|
| {{Box|1=| | | {<math> A(-1|{-}2|2) </math> und <math> B(-3|{-}1|0) </math>} |
| <quiz display="simple">
| | + <math> 3 </math> |
| {Gegeben ist ein Dreieck <math> ABC </math> mit den Punkten <math> A(-3|0|-2) </math> <math> B(1|2|2) </math> und <math> C(-3|3|2) </math> . Berechne den Umfang des Dreiecks.}
| | - <math> 6 </math> |
| - 14,123 | | - <math> 9 </math> |
| - 11,256 | | - <math> 12 </math> |
| + 15,123
| |
| - 13,894 | |
| </quiz> | | </quiz> |
| |3=Arbeitsmethode|Farbe={{Farbe|blau|dunkel}}}}
| | {{Lösung versteckt|1=Man berechtnet den Abstand zweier Punkte wie folgt: Man betrachtet die einzelnen Einträge von <math> A </math> und <math> B </math>. Wenn man sich den ersten Eintrag von <math> A </math> anschaut, so betrachtet man auch den ersten Eintrag von <math> B </math>. Zwischen diesen beiden Einträgen bildet man nun die Differenz. Gleiches Verfahren setzt man bei allen anderen Einträgen ein. Achtung: Betrachte immer nur von einem Punkt zum anderen die Veränderung, sodass sich keine Vorzeichenfehler einschleichen! Man betrachtet also immer alle Einträge von <math> A </math> nach <math> B </math> oder alle Einträge von <math> B </math> nach <math> A </math>. Dann hat man einen Vektor gefunnden, der die Verschiebung beschreibt. Ab hier geht man dann wieder so vor wie in Tipp 1 beschrieben|2=Tipp 2|3=Tipp verbergen}} |
| | |
| {{Box|1= ==Aufgabe 9 - Vektoren addieren und mit einem Skalar multiplizieren==
| |
| | |
| {{LearningApp|width=100%|height=500px|app=11071387}}
| |
| |3=Arbeitsmethode|Farbe={{Farbe|gelb|dunkel}}}} | |
|
| |
|
| ==Aufgabe 10: Lückentext - Geometrische Bedeutung von Vektoraddition und skalarer Multiplikation== | | |3=Arbeitsmethode|Farbe={{Farbe|orange}}}} |
|
| |
|
| <div class="lueckentext-quiz">
| | ==Geometrische Objekte untersuchen== |
| Wir definieren zwei '''Rechenoperationen''' für Vektoren: das Bilden des Vielfachen und der Summe. Die '''Vektoraddition''' bezeichnet das bilden der '''Summe''' zweier Vektoren gleichen Typs, das heißt dass die beiden Vektoren gleich viele '''Komponenten''' haben. Man bildet die Summe, indem man die '''Einträge''' der Vektoren '''komponentenweise''' addiert. Wir können uns die Addition von Vektoren als ein „'''Aneinanderlegen'''“ von zwei '''Strecken''' von ggf. verschiedener Länge vorstellen. Nennen wir <math> \vec{a} </math> und <math> \vec{b}</math> Vektoren. Wir deuten diese als '''Pfeile''' und addieren sie, das heißt wir legen sie hintereinander, sodass der '''Anfang''' von <math> \vec{b} </math> und die „'''Spitze'''“ von <math> \vec{a} </math> übereinstimmen. Ein derartiges Verhalten von Pfeilen ist aus der '''Physik''' bekannt. Dort werden oftmals '''Kräfte''' und Geschwindigkeiten mit Pfeilen dargestellt. Man kann am Ende zur Addition sagen, dass das Bilden der Summe zweier Vektoren a+b als '''Hintereinander-Ausführen''' der durch <math> \vec{a} </math> und <math> \vec{b} </math> dargestellten '''Verschiebungen''' gesehen werden kann.
| | {{Box|1= Aufgabe 8: Besondere Vierecke |
| | |2= |
|
| |
|
| Das Bilden des '''Vielfachen''' eines Vektors wird auch als '''Multiplikation mit einem Skalar''' bezeichnet. Wir nennen unseren '''Vektor''' wieder <math> \vec{a} </math> und das '''Skalar''' bezeichnen wir mit <math> c </math>. Von jedem Vektor kann das '''<math> c </math> -Fache''' gebildet werden, indem '''alle Komponenten''' von <math> \vec{a} </math> '''mit <math> c </math> multipliziert''' werden. Ist '''<math> c>0 </math>''' so wird der „Pfeil“ von <math> \vec{a} </math> um den Faktor <math> c </math> aufgeblasen ('''falls <math>c > 1</math>''') oder geschrumpft ('''falls <math>c < 1</math> '''). Ist '''<math>c<0</math>''', so erhält der Pfeil, der um den Faktor <math> c </math> aufgeblasen oder geschrumpft wird, noch eine '''Richtungsumkehrung''' und wird zum '''Gegenvektor'''.
| | In einem kartesischen Koordinatensystem sind die Punkte <math> A(3|3|5)</math>, <math> B(3{,}5|3{,}5|1)</math> und <math> C(6{,}5|2{,}5|3) </math> gegeben. |
| | |
| Wir nennen zwei Vektoren '''kollinear''' (oder parallel), wenn einer der Vektoren ein '''Vielfaches des anderen''' ist. Mit anderen Worten: Wenn <math> \vec{a} </math> und <math> \vec{b} </math> zwei '''verschiedene''' Vektoren sind, so sind sie '''parallel/kollinear''' zueinander, falls ein '''Skalar <math> c </math>''' existiert, sodass gilt: '''<math> ca=b </math>'''. Dabei ist es egal, ob die beiden Vektoren in '''unterschiedliche''' '''Richtungen''' zeigen oder nicht.
| |
| </div>
| |
| | |
| | |
| {{Box|1= Arbeitsmethode|2= ==Aufgabe 11 - Für die ganz Schnellen eine Knobelaufgabe: Besondere Vierecke==
| |
| | |
| In einem kartesischen Koordinatensystem sind die Punkte <math> A(3|3|5)</math>, <math> B(3,5|3,5|1)</math> und <math> C(6,5|2,5|3) </math> gegeben. | |
|
| |
|
| <quiz display="simple"> | | <quiz display="simple"> |
| Zeile 482: |
Zeile 171: |
|
| |
|
| <quiz display="simple"> | | <quiz display="simple"> |
| {b) Sei <math> P </math> nun ein weiter Punkt im bereits vorhandenen System. Welche Koordinaten muss <math> P </math> haben, damit <math> P </math> gemeinsam mit <math> A </math>, <math> B </math> und <math> C </math> die Eckpunkte einer Raute bildet?} | | {b) Wir betrachten weiterhin das Dreieck <math> ABC </math>. Ein neuer Punkt <math> Q </math> soll so gewählt werden, dass er zusammen mit dem Dreieck <math> ABC </math> ein Parallelogramm bildet, das keine Raute ist. Welche Koordinaten passen zu <math> Q </math>? Es sind zwei Antwortmöglichkeiten richtig. Finde beide!} |
| + <math> P(7|3|-1)</math> | | + <math> Q(6|2|7)</math> |
| - <math> P(-7|-3|1)</math> | | - <math> Q(7|4|3)</math> |
| - <math> P(5|2|-3)</math> | | + <math> Q(0|4|3)</math> |
| - <math> P(-5|-2|3)</math> | | - <math> Q(6|3|{-}1)</math> |
| | </quiz> |
| | {{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist. |2=Tipp 1|3=Tipp verbergen}} |
| | {{Lösung versteckt|1=Du musst Gegenvektoren verwenden.|2=Tipp 2|3=Tipp verbergen}} |
| | {{Lösung versteckt|1=Verwende den Vektor <math>\vec{ CA }</math> am Punkt <math> B </math> für eines der Parallelogramme und den Vektor <math>\vec{ BA } </math> am Punkt <math> C </math> für das zweite Parallelogramm.|2=Tipp 3|3=Tipp verbergen}} |
| | |
| | <quiz display="simple"> |
| | {c) Sei <math> P </math> nun ein weiter Punkt im bereits vorhandenen System. Welche Koordinaten muss <math> P </math> haben, damit <math> P </math> gemeinsam mit <math> A </math>, <math> B </math> und <math> C </math> die Eckpunkte einer Raute bildet?} |
| | + <math> P(7|3|{-}1)</math> |
| | - <math> P(-7|{-}3|1)</math> |
| | - <math> P(5|2|{-}3)</math> |
| | - <math> P(-5|{-}2|3)</math> |
| </quiz> | | </quiz> |
| {{Lösung versteckt|1=Zeichne dir ein gleichschenkliges Dreieck auf und mach dir zunächst klar welche Seite die Basis des Dreieicks ist.|2=Tipp 1|3=Tipp verbergen}} | | {{Lösung versteckt|1=Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist.|2=Tipp 1|3=Tipp verbergen}} |
| {{Lösung versteckt|1=Gegenüberliegende Seiten sind in einer Raute gleich lang.|2=Tipp 2|3=Tipp verbergen}} | | {{Lösung versteckt|1= In einer Raute sind alle Seiten gleich lang und gegenüberliegende Seiten parallel.|2=Tipp 2|3=Tipp verbergen}} |
| {{Lösung versteckt|1=Verwende den Vektor <math>\vec{ AC }</math> am Punkt <math> B </math>.|2=Tipp 3|3=Tipp verbergen}} | | {{Lösung versteckt|1= Verwende den Vektor <math>\vec{ AC }</math> am Punkt <math> B </math>.|2=Tipp 3|3=Tipp verbergen}} |
|
| |
|
| <quiz display="simple">
| | |3= Arbeitsmethode|Farbe={{Farbe|orange}}}} |
| {c) wir betrachten nun wieder das Dreieck <math> ABC </math>. Ein neuer Punkt <math> Q </math> solls o gewählt werden, dass er zusammen mit dem Dreieck <math> ABC </math> ein Parallelogramm bildet, das keine Raute ist. Welche Koordinaten passen zu <math> Q </math>? Es sind zwei Antwortmöglichkeiten richtig. Finde beide!}
| | |
| + <math> P(6|2|7)</math>
| | {{Fortsetzung|vorher=zurück zur Kapitelauswahl|vorherlink=Digitale_Werkzeuge_in_der_Schule/Unterwegs_in_3-D_–_Punkte,_Vektoren,_Geraden_und_Ebenen_im_Raum#Kapitelauswahl}} |
| - <math> P(7|4|3)</math>
| | |
| + <math> P(0|4|3)</math>
| | {{SORTIERUNG:{{SUBPAGENAME}}}} |
| - <math> P(6|3|-1)</math>
| | [[Kategorie:Digitale Werkzeuge in der Schule]] |
| </quiz>
| |
| {{Lösung versteckt|1=Zeichne dir ein gleichschenkliges Dreieck auf <math> ABC </math> und überleg dir wie ein Parallelogram entstehen könnte. |2=Tipp 1|3=Tipp verbergen}} | |
| {{Lösung versteckt|1=Sei dir bewusst, dass es auch Gegenvektoren gibt.|2=Tipp 2|3=Tipp verbergen}} | |
| {{Lösung versteckt|1=Verwende den Vektor <math>\vec{ CA }</math> am Punkt <math> B </math> und den Vektor <math>\vec{ BA } </math> am Punkt <math> C </math>.|2=Tipp 3|3=Tipp verbergen}} | |
| |3= Arbeitsmethode|Farbe={{Farbe|grün|dunkel}}}}
| |