Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum
In diesem Lernpfadkapitel beschäftigst du dich mit Geraden im Raum. Du lernst, Geraden im Raum durch Vektoren zu beschreiben, Parameterdarstellungen und Spurpunkte von Geraden zu bestimmen, die Lage von Geraden im Raum und zueinander zu bestimmen sowie Geradenscharen zu bestimmen.
Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:
- Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit
- und Aufgaben mit grünem Streifen sind Knobelaufgaben.
Einführung
Parameterdarstellung einer Geraden
Lagebeziehungen von Geraden
Wir unterscheiden die Lage zweier Geraden in identisch, parallel, geschnitten und windschief. Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander kollinear (sind Vielfache voneinander), so können die Geraden lediglich identisch oder parallel sein.
Um nun zu untersuchen, ob die Geraden parallel oder identisch sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden identisch. Andernfalls sind die Geraden echt parallel.
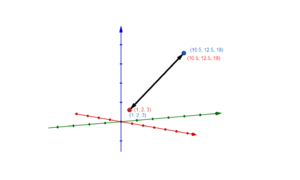
Wie verlaufen die folgenden Geraden zueinander?
a)

b)

c)

 ein Vielfaches voneinander (=kollinear) sind. Da beide Ortsvektoren identisch sind, sind die Geraden identisch.
ein Vielfaches voneinander (=kollinear) sind. Da beide Ortsvektoren identisch sind, sind die Geraden identisch. nicht auf der Geraden von
nicht auf der Geraden von , mit
, mit  .
. ) und der Ortsvektor der einen Gerade auf der anderen Gerade ist:
) und der Ortsvektor der einen Gerade auf der anderen Gerade ist:  .
.
Sind die Richtungsvektoren nicht kollinear, so können die Geraden sich lediglich schneiden oder windschief zueinander sein.
Um nun zu untersuchen, ob sich die Geraden schneiden oder zueinader winschief sind, müssen wir schauen, ob sich ein Schnittpunkt berechnen lässt. Hierzu setzen wir die Geradengleichungen gleich und formen um. Erhalten wir einen Schnittpunkt S, so schneiden sich die Geraden im Punkt S. Andernfalls sind diese Geraden windschief zueinander.
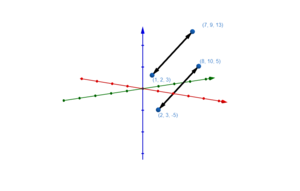
Wie verlaufen die folgenden Geraden zueinander?
a)

b)

c)

Zwei Geraden...
sind identisch
- Richtungsvektoren kollinear (= Vielfache voneinander)
- Ortsvektor der einen Geraden liegt auf der anderen Geraden
sind parallel
- Richtungsvektoren kollinear (= Vielfache voneinander)
- Ortsvektor der einen Geraden liegt nicht auf der anderen Geraden.
schneiden sich
- Richtungsvektoren nicht kollinear (= Vielfache voneinander)
- Bei dem Versuch einen Schnittpunkt zu berechnen, kommt eine wahre Aussage in Form eines Punktes heraus
sind zueinander windschief
- Richtungsvektoren nicht kollinear (= Vielfache voneinander)
- Bei dem Versuch einen Schnittpunkt zu berechnen, kommt eine falsche Aussage heraus
.
Flugerlaubnis erteilen?
Ein wichtiger Bestandteil der Flugsicherung sind die Fluglotsen der "Deutschen Flugsicherung" (DFS). Sie koordinieren und überwachen jährlich Millionen Flüge im deutschen Luftraum. Am heutigen Tag wollen drei Flugzeuge starten. Hierzu gehört das Fugzeug der Marke Aer startet bei 



Es kam zu einem riesigen Stromausfall und der Fluglotse ist sich unsicher. Hilf ihm die Antworten auf folgende Fragen zu finden:
a) Wie lauten die Geradengleichungen der einzelen Fugzeuge?
b) Welches der Flugzeuge ist das schnellste?
c) Können alle Flugzeuge starten, ohne dass es zu einer Kollision kommt?
Flugzeug Aer:

Dies erhalten wir, indem wir folgendes berechnen:

Flugzeug Amadeus:

Dies erhalten wir wie folgt:
Wir wiisen, dass sich das Flugzeug nach einer Sekunde bei 


![{\displaystyle 164,85={\sqrt[{2}]{98,88**2+82,4**2+z**2}}}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/3c8b6cc3f237dd69aa0895ca9690f6a18dfc24e0)

Wir berechnen die Geschwindigkeit, indem wir die Länge des Richtungsvektors berechnen. Dies erfolgt it der Formel:

Flugzeug Aer und Amadeus:
Sie schneiden sich für