Digitale Werkzeuge in der Schule/Mathematik im Beruf/Tischlerinnen und Tischler: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 42: | Zeile 42: | ||
Notiere dir die Rechnungen für die folgenden Aufgaben in deinem Heft bzw. auf deinem Tablet. | Notiere dir die Rechnungen für die folgenden Aufgaben in deinem Heft bzw. auf deinem Tablet. | ||
{{Box|Aufgabe 5: Dachstütze| [[Datei:Dreieck_Holz.jpg|rechts|mini|Die Dachstütze]] | |||
a) Zuerst sollst du ein Bauteil für einen Dachstuhl verleimen und zwar als rechtwinkliges Dreieck. Die Längen der Holzbalken sollst du an der Konstruktion abmessen. Du hast die Längen <math>3</math> dm, <math>4</math> dm und <math>5</math> dm abgemessen. Zeige, dass du mit diesen Längen ein rechtwinkliges Dreieck konstruieren kannst. | |||
a) Zuerst sollst du ein Bauteil für einen Dachstuhl verleimen und zwar als rechtwinkliges Dreieck. Die Längen der Holzbalken sollst du an der Konstruktion abmessen. Du hast die Längen <math>3</math> dm, <math>4</math> dm und <math>5</math> dm abgemessen. Zeige, dass du mit diesen Längen ein rechtwinkliges Dreieck konstruieren kannst. | {{Lösung versteckt | Setze zwei Seitenlängen des Dreiecks in den Satz des Pythagoras ein und überprüfe. Überlege zuerst, welche Seiten die Katheten sind und welche die Hypotenuse ist.| Tipps anzeigen | Tipps verbergen}} | ||
{{Lösung versteckt |1= Die längste Seite ist die Hypotenuse, also haben wir <math>c = 5</math> dm und die beiden anderen Seiten sind die Katheten mit <math>a = 3</math> dm und <math>b = 4</math> dm. Also muss gelten: | {{Lösung versteckt |1= Die längste Seite ist die Hypotenuse, also haben wir <math>c = 5</math> dm und die beiden anderen Seiten sind die Katheten mit <math>a = 3</math> dm und <math>b = 4</math> dm. Also muss gelten: | ||
| Zeile 68: | Zeile 68: | ||
[[Datei:Skizze Aufgabe 2.jpg|mini|Die geplante Kopfbandkonstruktion]] | [[Datei:Skizze Aufgabe 2.jpg|mini|Die geplante Kopfbandkonstruktion]] | ||
b) Für eine Kopfbandkonstruktion nennt dir Herr Meier eine Höhe von <math>45</math> cm und Breite von <math>45</math> cm. Du sollst nun das Kopfband zuschneiden. Die Länge dessen ist nicht bekannt und die gesamte Konstruktion muss noch angefertigt werden, sodass du die Länge nicht ausmessen kannst. Berechne die Länge des Kopfbandes. | b) Für eine Kopfbandkonstruktion nennt dir Herr Meier eine Höhe von <math>45</math> cm und Breite von <math>45</math> cm. Du sollst nun das Kopfband zuschneiden. Die Länge dessen ist nicht bekannt und die gesamte Konstruktion muss noch angefertigt werden, sodass du die Länge nicht ausmessen kannst. Berechne die Länge des Kopfbandes. | ||
{{Lösung versteckt | Die gesuchte Seite ist die Hypotenuse.| Tipps anzeigen | Tipps verbergen}} | {{Lösung versteckt | Die gesuchte Seite ist die Hypotenuse.| Tipps anzeigen | Tipps verbergen}} | ||
{{Lösung versteckt |<math>\begin{align} | {{Lösung versteckt |<math>\begin{align} | ||
& & 45^2 + 45^2 &= c^2 | & & 45^2 + 45^2 &= c^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & 4050 &= c^2 | \Leftrightarrow & & 4050 &= c^2 & &\mid \surd\\ | ||
\Leftrightarrow & & \sqrt{4050} &= c | \Leftrightarrow & & \sqrt{4050} &= c \\ | ||
\Leftrightarrow & & c &\approx 63{,}6396 | \Leftrightarrow & & c &\approx 63{,}6396 | ||
\end{align}</math>| 2=Lösung anzeigen | 3=Lösung verbergen}} | \end{align}</math>| 2=Lösung anzeigen | 3=Lösung verbergen}} | ||
|Arbeitsmethode | Farbe=#CD2990 }} | |Arbeitsmethode | Farbe=#CD2990 }} | ||
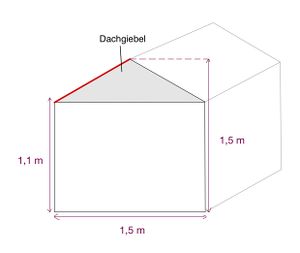
{{Box|Aufgabe 6: Gartenhäuschen| Im Garten soll ein Spielhäuschen aufgebaut werden. Als Dach sollen zwei Holzplatten dienen, die jeweils rechts und links an den Dachgiebel angebracht werden. Berechne wie lang die rot makierte Seite der Holzplatte sein muss, wenn das Häuschen insgesamt <math>1,5</math> m breit und <math>1,5</math> m hoch ist. Die Höhe des Häuschens ohne das Dach beträgt <math>1,10</math> m. [[Datei:Skizze Aufgabe 4.jpg|mini|Der Plan des Gartenhäuschens]] | {{Box|Aufgabe 6: Gartenhäuschen| Im Garten soll ein Spielhäuschen aufgebaut werden. Als Dach sollen zwei Holzplatten dienen, die jeweils rechts und links an den Dachgiebel angebracht werden. Berechne wie lang die rot makierte Seite der Holzplatte sein muss, wenn das Häuschen insgesamt <math>1{,}5</math> m breit und <math>1{,}5</math> m hoch ist. Die Höhe des Häuschens ohne das Dach beträgt <math>1{,}10</math> m. [[Datei:Skizze Aufgabe 4.jpg|mini|Der Plan des Gartenhäuschens]] | ||
{{Lösung versteckt | Überlege wo du in diesem Konstrukt ein rechtwinkliges Dreieck findest, was dir zur Berechung helfen kann.| Tipp 1 anzeigen | Tipp 1 verbergen}} | {{Lösung versteckt | Überlege wo du in diesem Konstrukt ein rechtwinkliges Dreieck findest, was dir zur Berechung helfen kann.| Tipp 1 anzeigen | Tipp 1 verbergen}} | ||
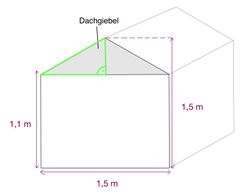
{{Lösung versteckt |Das gefragte Dreieck ist in grün eingezeichnet. Überlege, welche Längen der Seiten des Dreiecks du dir aus den Beschriftungen erschließen kannst. [[Datei:Rechtwinkliges Dreieck Dachgiebel.jpg|mini|zentriert|250px|Rechtwinkliges Dreieck im Dachgiebel]]| Tipp 2 anzeigen | Tipp 2 verbergen}} | {{Lösung versteckt |Das gefragte Dreieck ist in grün eingezeichnet. Überlege, welche Längen der Seiten des Dreiecks du dir aus den Beschriftungen erschließen kannst. [[Datei:Rechtwinkliges Dreieck Dachgiebel.jpg|mini|zentriert|250px|Rechtwinkliges Dreieck im Dachgiebel]]| Tipp 2 anzeigen | Tipp 2 verbergen}} | ||
{{Lösung versteckt | | {{Lösung versteckt | | ||
Wir betrachten die waagerechte Seite <math> a = 75 </math>cm und die senkrechte Seite <math> b = 40 </math>cm. Diese Längen setzen wir in den Satz des Pythagoras ein: | Wir betrachten die waagerechte Seite <math> a = 75 </math>cm und die senkrechte Seite <math> b = 40 </math>cm. Diese Längen setzen wir in den Satz des Pythagoras ein: | ||
<math>\begin{align} | <math>\begin{align} | ||
& & 40^2 + 75^2 &= c^2 | & & 40^2 + 75^2 &= c^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & 7225 &= c^2 | \Leftrightarrow & & 7225 &= c^2 & &\mid \surd\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & 85 &= c | ||
\end{align}</math> | \end{align}</math> | ||
Also ist die gefragte Länge <math>85</math> cm.| 2=Lösung anzeigen | 3=Lösung verbergen}}|Arbeitsmethode | Farbe=#CD2990 }} | Also ist die gefragte Länge <math>85</math> cm.| 2=Lösung anzeigen | 3=Lösung verbergen}}|Arbeitsmethode | Farbe=#CD2990 }} | ||
{{Box|1=Info|2= Bei Aufgabe 7 musst du nur entweder Aufgabe 7a <u>oder</u> Aufgabe 7b bearbeiten. Beachte, dass die Aufgaben 7a und 7b verschiedene Schwierigkeitsstufen haben.|3=Kurzinfo}} | {{Box|1=Info|2= Bei Aufgabe 7 musst du nur entweder Aufgabe 7a <u>oder</u> Aufgabe 7b bearbeiten. Beachte, dass die Aufgaben 7a und 7b verschiedene Schwierigkeitsstufen haben.|3=Kurzinfo}} | ||
| Zeile 98: | Zeile 99: | ||
{{Box|Aufgabe 7a: Eckschrank|Nach den Arbeiten im Garten seid ihr nun wieder im Wohnzimmer. Hier soll ein Eckschrank konstruiert werden. Die Tür dieses Schranks soll in der Mitte zu öffnen sein und dann zu beiden Seiten aufgehen. Der Schrank endet an den Wänden jeweils <math>35</math> cm von der Zimmerecke entfernt. | {{Box|Aufgabe 7a: Eckschrank|Nach den Arbeiten im Garten seid ihr nun wieder im Wohnzimmer. Hier soll ein Eckschrank konstruiert werden. Die Tür dieses Schranks soll in der Mitte zu öffnen sein und dann zu beiden Seiten aufgehen. Der Schrank endet an den Wänden jeweils <math>35</math> cm von der Zimmerecke entfernt. | ||
Fertige zunächst eine Skizze an. Berechne dann die Länge einer Tür. Da das Ergebnis sehr genau sein muss, runde auf drei Nachkommastellen. | Fertige zunächst eine Skizze an. Berechne dann die Länge einer Tür. Da das Ergebnis sehr genau sein muss, runde auf drei Nachkommastellen. | ||
{{Lösung versteckt | Zur genaueren Vorstellung der Konstruktion siehe dir die Skizze "Eckschrank" an. [[Datei:Eckschrank.jpg|alternativtext=|zentriert|mini|387x387px|Eckschrank]]| Tipps anzeigen | Tipps verbergen}} | {{Lösung versteckt | Zur genaueren Vorstellung der Konstruktion siehe dir die Skizze "Eckschrank" an. [[Datei:Eckschrank.jpg|alternativtext=|zentriert|mini|387x387px|Eckschrank]]| Tipps anzeigen | Tipps verbergen}} | ||
{{Lösung versteckt |1= Die gesuchte Länge ist die Hälfte der Hypotenuse. Wir berechnen zunächst die gesamte Länge der Hypotenuse mit Hilfe des Satz des Pythagoras: | {{Lösung versteckt |1= Die gesuchte Länge ist die Hälfte der Hypotenuse. Wir berechnen zunächst die gesamte Länge der Hypotenuse mit Hilfe des Satz des Pythagoras: | ||
<math>\begin{align} | <math>\begin{align} | ||
& & 35^2 + 35^2 &= c^2 | & & 35^2 + 35^2 &= c^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & 2450 &= c^2 | \Leftrightarrow & & 2450 &= c^2 & &\mid \surd\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & 49{,}497 &\approx c | ||
\end{align}</math> | \end{align}</math> | ||
Da nur nach der Länge einer Tür gefragt ist, müssen wir das Ergebnis noch durch zwei teilen. | Da nur nach der Länge einer Tür gefragt ist, müssen wir das Ergebnis noch durch zwei teilen. | ||
<math> | <math>49{,}497 : 2 = 24{,}749</math> | ||
Also beträgt die Länge einer Tür <math>24,749</math> cm. | Also beträgt die Länge einer Tür <math>24{,}749</math> cm. | ||
| 2=Lösung anzeigen | 3=Lösung verbergen}} |Arbeitsmethode}} | | 2=Lösung anzeigen | 3=Lösung verbergen}} |Arbeitsmethode}} | ||
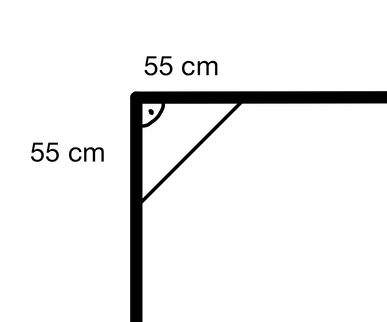
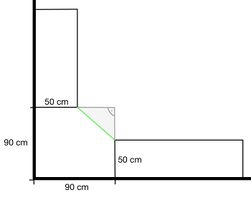
{{Box|1= ⭐ Aufgabe 7b: Eckschrank zwischen Schränken|2=Es soll ein Eckschrank gebaut werden. Dieser hat allerdings die Besonderheit, dass er sich zwischen zwei bereits vorhandenen Schränken befinden soll. Diese stehen jeweils <math>90</math> cm von der Zimmerecke entfernt und sind jeweils <math>50</math> cm breit. Der Eckschrank soll eine durchgängige Tür haben, die von dem einen Schrank zum anderen reicht. Berechne die Länge dieser Schranktür. Runde auf drei Nachkommestellen. | {{Box|1= ⭐ Aufgabe 7b: Eckschrank zwischen Schränken|2=Es soll ein Eckschrank gebaut werden. Dieser hat allerdings die Besonderheit, dass er sich zwischen zwei bereits vorhandenen Schränken befinden soll. Diese stehen jeweils <math>90</math> cm von der Zimmerecke entfernt und sind jeweils <math>50</math> cm breit. Der Eckschrank soll eine durchgängige Tür haben, die von dem einen Schrank zum anderen reicht. Berechne die Länge dieser Schranktür. Runde auf drei Nachkommestellen. | ||
{{Lösung versteckt | [[Datei:Eckschrank zwischen zwei Schränken.jpg|rechts|mini|x200px|Eckschrank zwischen zwei Schränken]] Die grün markierte Seite ist die gesuchte Länge. Man denkt sich das grau gezeichnete rechtwinklige Dreieck dazu, ermittelt die Werte dieser und kann dann den Satz des Pythagoras anwenden. | {{Lösung versteckt | [[Datei:Eckschrank zwischen zwei Schränken.jpg|rechts|mini|x200px|Eckschrank zwischen zwei Schränken]] Die grün markierte Seite ist die gesuchte Länge. Man denkt sich das grau gezeichnete rechtwinklige Dreieck dazu, ermittelt die Werte dieser und kann dann den Satz des Pythagoras anwenden. | ||
| Tipps anzeigen | Tipps verbergen}} | |||
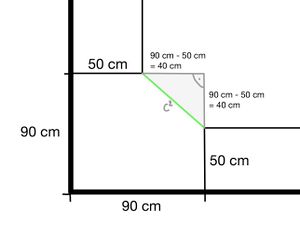
{{Lösung versteckt |[[Datei:Lösung A7.jpg||rechts|mini|Lösungsskizze Aufgabe 7]] In der Skizze sehen wir das rechtwinklinge Dreieck, welches man zur Berechnung der grün markierten Seite konsturiert hat. Durch rechnen mit den gegebenen Werten finden wir für dieses Dreieck die notwendigen Maße. Diese betragen an beiden Seiten <math>40</math> cm. Mit diesen wenden wir dann den Satz des Pythagoras an: | {{Lösung versteckt |[[Datei:Lösung A7.jpg||rechts|mini|Lösungsskizze Aufgabe 7]] In der Skizze sehen wir das rechtwinklinge Dreieck, welches man zur Berechnung der grün markierten Seite konsturiert hat. Durch rechnen mit den gegebenen Werten finden wir für dieses Dreieck die notwendigen Maße. Diese betragen an beiden Seiten <math>40</math> cm. Mit diesen wenden wir dann den Satz des Pythagoras an: | ||
<math>\begin{align} | <math>\begin{align} | ||
& & 40^2 + 40^2 &= c^2 | & & 40^2 + 40^2 &= c^2 & &\mid \text{Termumformung}\\ | ||
\Leftrightarrow & & 3200&= c^2 | \Leftrightarrow & & 3200 &= c^2 & &\mid \surd\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & 56{,}569 &\approx c | ||
\end{align}</math> | \end{align}</math> | ||
Somit beträgt die Länge der Schranktür <math>56,569</math> cm. | Somit beträgt die Länge der Schranktür <math>56{,}569</math> cm. | ||
| 2=Lösung anzeigen | 3=Lösung verbergen}} | | 2=Lösung anzeigen | 3=Lösung verbergen}} | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
{{Box | Aufgabe 8: Schrankaufbau | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Bearbeite nun auf deinem '''Arbeitsblatt''' die Aufgabe "Schrankaufbau"|Arbeitsmethode| Farbe=#CD2990 }} | |||
{{Lösung versteckt |Um die maximale Höhe des Schrankes herauszufinden, darf die Diagonale dessen höchstens der Deckenhöhe entsprechen, damit der Schrank problemlos aufgerichtet werden kann. Für das rechtwinklige Dreieck, welches von der Diagonale des Schrankes gebildet wird, ist die Länge der Hypotenuse also <math>2{,}40</math> m und die Länge der einen Kathete <math>50</math> cm gegeben. <math>2{,}40</math> m entsprechen <math>240</math> cm. Wir suchen also die Länge der zweiten Kathete und berechnen sie mithilfe des Satz des Pythagoras: | |||
{{Lösung versteckt |Um die maximale Höhe des Schrankes herauszufinden, darf die Diagonale dessen höchstens der Deckenhöhe entsprechen, damit der Schrank problemlos aufgerichtet werden kann. Für das rechtwinklige Dreieck, welches von der Diagonale des Schrankes gebildet wird, ist die Länge der Hypotenuse also <math>2,40</math> m und die Länge der einen Kathete <math>50</math> cm gegeben. <math>2,40</math> m entsprechen <math>240</math> cm. Wir suchen also die Länge der zweiten Kathete und berechnen sie mithilfe des Satz des Pythagoras: | |||
<math>\begin{align} | <math>\begin{align} | ||
& & 50^2 + b^2 &= 240^2 | & & 50^2 + b^2 &= 240^2 & &\mid -50 ^ 2\\ | ||
\Leftrightarrow & & b^2 &= 240^2 - 50^2 | \Leftrightarrow & & b^2 &= 240^2 - 50^2 \\ | ||
\Leftrightarrow & & b^2 &= 55100 | \Leftrightarrow & & b^2 &= 55100 & &\mid \surd\\ | ||
\Leftrightarrow & & | \Leftrightarrow & & b &\approx 234{,}734 | ||
\end{align}</math> | \end{align}</math> | ||
Die Höhe des Schrankes darf somit maximal <math>234,734</math> cm, also <math>2,3473</math> m hoch sein. | Die Höhe des Schrankes darf somit maximal <math>234{,}734</math> cm, also <math>2{,}3473</math> m hoch sein. | ||
| 2=Lösung anzeigen | 3=Lösung verbergen}} | | 2=Lösung anzeigen | 3=Lösung verbergen}} | ||
{{Box | Aufgabe 9: Leitfrage beantworten | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Bearbeite danach auf dem '''Arbeitsblatt''' die Aufgabe "Leitfrage beantworten"| Arbeitsmethode | Farbe=#CD2990 }} | {{Box | Aufgabe 9: Leitfrage beantworten | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] Bearbeite danach auf dem '''Arbeitsblatt''' die Aufgabe "Leitfrage beantworten"| Arbeitsmethode | Farbe=#CD2990 }} | ||
{{Fortsetzung|weiter=weiter zum nächsten Kapitel|weiterlink=Digitale Werkzeuge in der Schule/Mathematik im Beruf/Kaufmännische Berufe}} | {{Fortsetzung|weiter=weiter zum nächsten Kapitel|weiterlink=Digitale Werkzeuge in der Schule/Mathematik im Beruf/Kaufmännische Berufe}} | ||
Version vom 2. Mai 2023, 12:01 Uhr
Der Beruf der Tischlerin und des Tischlers
Dein Praktikum bei Herrn Meier
Herr Meier ist Tischler. Weil du dich für den Beruf des Tischlers oder der Tischlerin interessierst, begleitest du ihn heute bei seiner Arbeit. Ihr besucht heute ein Grundstück, für das Herr Meier gerade zuständig ist. Dabei müsst ihr einige fertige Möbel aufbauen und anbringen sowie neue Konstruktionen planen.
Vorwissen
Um Herrn Meier behilflich zu sein, musst du dich an einige Inhalte aus dem Mathematikunterricht erinnern. Bearbeite dazu die folgenden Aufgaben.
Aufgaben im Praktikum
Jetzt geht es los: An deinem Praktikumstag hat Herr Meier einige Aufgaben für dich. Notiere dir die Rechnungen für die folgenden Aufgaben in deinem Heft bzw. auf deinem Tablet.
Um die maximale Höhe des Schrankes herauszufinden, darf die Diagonale dessen höchstens der Deckenhöhe entsprechen, damit der Schrank problemlos aufgerichtet werden kann. Für das rechtwinklige Dreieck, welches von der Diagonale des Schrankes gebildet wird, ist die Länge der Hypotenuse also m und die Länge der einen Kathete cm gegeben. m entsprechen cm. Wir suchen also die Länge der zweiten Kathete und berechnen sie mithilfe des Satz des Pythagoras:
Die Höhe des Schrankes darf somit maximal cm, also m hoch sein.