Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
(erste Inhalte eingefügt) |
(verbesserung im Layout und Text) |
||
| Zeile 1: | Zeile 1: | ||
{{Box|Lernpfad: von der durchschnittlichen zur lokalen Änderungsrate|Dieser Lernpfad bietet Dir einen Einstieg in das Thema Differenzialrechnung. | {{Box|Lernpfad: von der durchschnittlichen zur lokalen Änderungsrate|Dieser Lernpfad bietet Dir einen Einstieg in das Thema Differenzialrechnung. | ||
Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du | Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du selbständig die Aufgaben bearbeiten.Du benötigst Papier und Stifte, Lineal und Taschenrechner. Die Aufgaben haben 3 unterschiedliche Schwierigkeitsstufen, die farblich gekennzheichnet sind: | ||
- '''Schwierigkeitsstufe I mit gelben Titel''': sind leichte Verständnis- und Rechenaufgaben zum Einstieg | |||
- '''Schwierigkeitsstufe II mit blauen Titel''': normale, mittelschwere Aufgaben zum üben und vertiefen. | |||
Anschaulich ist dies die Steigung der Sekante der Funktion zwischen den Punkten <math>x_0</math> und <math>x_1</math>, Du kennst diese Formel bereits als Berechnung der Steigung | - '''Schwierigkeitsstufe III mit grünen Titel''': herausfordernde Aufgaben | ||
Viel Erfolg!|Kurzinfo}} | |||
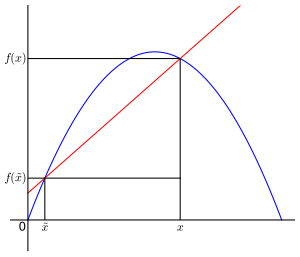
{{Box|Grundbegriffe: durchschnittliche Änderungsrate und Sekante|Die durchschnittliche Änderungsrate einer Funktion <math>f(x)</math> bezieht sich immer auf ein bestimmtes Intervall <math>[\tilde{x},x]</math>und wird mit Hilfe des '''Differenzenquotienten''' berechnet: | |||
<math>\frac{f(x) - f(\tilde{x})}{x-\tilde{x}}</math> | |||
Anschaulich ist dies die '''Steigung der Sekante '''der Funktion zwischen den Punkten <math>x_0</math> und <math>x_1</math>, Du kennst diese Formel bereits als Berechnung der Steigung einer linearen Funktion. | |||
Die Sekante (der Begriff bedeutet aus dem Lateinischen übersetzt die Schneidende) ist eine Gerade, die durch mindestens 2 Punkte eines Funktionsgraphen verläüft, ihn also an mind. 2 Punkten schneidet: | Die Sekante (der Begriff bedeutet aus dem Lateinischen übersetzt die Schneidende) ist eine Gerade, die durch mindestens 2 Punkte eines Funktionsgraphen verläüft, ihn also an mind. 2 Punkten schneidet: | ||
[[Datei:Sekantensteigung.svg|300px|links|rahmenlos|mini]] | [[Datei:Sekantensteigung.svg|300px|links|rahmenlos|mini]] | ||
| Zeile 30: | Zeile 37: | ||
[[Datei:Bild 109 V - starke Steigung, StVO DDR 1977.svg|200px|links|rahmenlos|mini]] | [[Datei:Bild 109 V - starke Steigung, StVO DDR 1977.svg|200px|links|rahmenlos|mini]] | ||
Der Verkehrszeichen gibt an, dass der durchschnittlicher Höhenunterschied (also die durchschnittliche Änderungsrate) auf dieser Strecke 10 Höhenmeter pro 100m Wegstrecke beträgt. Die Strasse selbst verläuft natürlich nicht als exakt gerade Linie. | |||
| | |||
{{Box|Grundbegriffe: lokale Änderungsrate und Tangente|hier auch Text| | Der Verkehrszeichen gibt an, dass der durchschnittlicher Höhenunterschied (also die durchschnittliche Änderungsrate) auf dieser Strecke 10 Höhenmeter pro 100m Wegstrecke beträgt. Die echte Strasse selbst verläuft natürlich nicht als exakt gerade Linie mit einer konstanten Steigung. | ||
|class}} | |||
{{Box|Grundbegriffe: lokale Änderungsrate und Tangente|hier auch Text|class}} | |||
Version vom 10. April 2020, 10:40 Uhr