Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Ableitung im Sachkontext anwenden

Merke

Die Aufgaben auf dieser Seite unterscheiden sich in ihrem Lernschwerpunkt und Schwierigkeitsgard:

• Falls du noch Probleme bei dem allgemeine Zuordnen der Ableitungsbegriffe zu den Anwendungskontexten hast konzentriere dich auf Aufgabe 2 & 3
• Für einen leichten Einstieg in die Sachkontexte befasse dich zunächst mit Aufgabe 1
• Komplexere Aufgaben befinden sich bei den Aufgaben 4 bis 7, wobei diese sich mit der Nummer in ihrer Schwierigkeit steigern. Solltest du schon sehr sicher mit den Aufgaben sein, gehe direkt zu Aufgabe 7

Vorlage:Arbeiten

a) Wie schnell ist Herr Müller auf seinem Weg zur Arbeit im Durchschnitt gefahren?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.

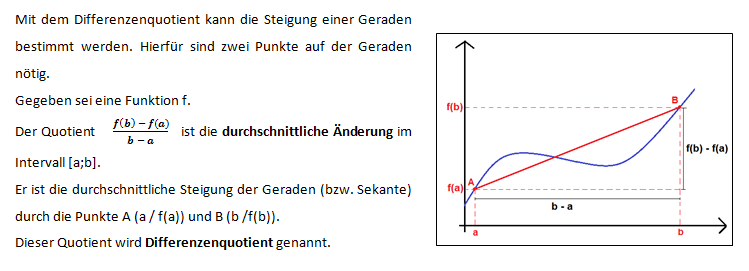
<popup name="Was genau ist der Differenzenquotient">

</popup>

<popup name="Lösung"> 24,5 km/h </popup>

b) Auf seinem Weg musst Herr Müller vor einer roten Ampel warten. Wann war das?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
<popup name="Lösung"> Er steht von Minute 5 bis 7 vor der Ampel und die Steigung des Graph ist in dieser Zeit 0. </popup>

c) Beschreibe den Fahrtverlauf der ersten 12 Minuten stichpunktartig.
<popup name="Hilfestellung"> Schau dir den Graphen Stück für Stück an. Wie ist die Steigung (positiv, negativ, null) und was bedeutet dies im Sachzusammenhang?
<popup name="genauere Hilfestellung"> Eine positive Steigeung bedeutet, dass Herr Müller mit seinem Auto fährt. Ist die Steigung stark, so fährt er eine lange Strecke in kurzer Zeit, d.h. er fährt schnell.
Ist die Steigung schwach, fährt er langsam.
Ist die Steigung Null (siehe Aufgabe b)) steht das Atuo.
Eine negative Steigung macht in diesem Zusammenhang nicht so viel Sinn, da ein Fahrtenschreiber, selbst wenn Herr Müller nach hause zurück fahren würde, aufschreibt, dass das Atuo vorwärts fährt. </popup> <popup name="Lösung">

• Minute 0-2: Steigung ist relativ schwach. → Herr Müller fährt langsam
  
• Mintuen 3-5: etwas stärkere Steigung → Herr Mülelr fährt schneller
  
• Minute 5-7: Steigung ist Null → Herr Müller steht mit seinem Auto (vor einer Ampel)
  
• Minute 7-12: Steigung nimmt zu → Herr Müller wird immer schneller </popup>
  

Vorlage:Arbeiten a) Den Flug des Balls kannst du unter folgendem Link genauer betrachten. Lass hierzu den roten Ball fliegen, indem du bei dem roten Ball auf play drücken. Die anderen Punkte solltest du nicht bewegen!

https://ggbm.at/J94wAFh3

b) Bestimme die Steigung des Balls an den verschiedenen Punkten der Flugkurve.

<popup name="Lösung"> bei A= 0,8; bei B=0; bei C=-0,8 </popup>

c) Ordne die Begriffe und Interpretationen den Markierungen auf dem Graphen zu. Hierzu musst die verschiedenen Markierungen anklicken und anschließend eine der vorgeschlagenen Möglichkeiten auswählen.

d) Fülle die Lücken, indem du die Aufgabe im Sachzusammenhang interpretieren.

Vorlage:Arbeiten

Vorlage:Arbeiten
a) Berechne den Funktionswert von f an der Stelle t=30 und interpretiere das Ergebnis im Sachzusammenhang.
<popup name="Lösung"> f(30)=0,83 Die Fichte wächst im 30. Jahr 83cm. </popup>

b) Bestimme rechnerisch das Alter, in dem die Fichte am stärksten wächst, und gib die größte Wachstumsgeschwindigkeit an. <popup name="Hilfestellung 1"> Extrempunkt (Hochpunkt) </popup> <popup name="Hilfestellung 2"> Ansatz: notwendige Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösung"> Der Hochpunkt liegt bei t=20 und die Wachstumsgeschwindigkeit beträgt 1,1 Meter. </popup>

Vorlage:Arbeiten

a) Berechne die Höhe des Wasserstandes um 7:30 Uhr. <popup name="Hilfestellung"> t=7,5 </popup> <popup name="Lösung"> h(7,5)=...≈10,37 </popup>

b) Berechne die Geschwindigkeit, mit der der Wasserstand in den ersten acht Stunden des Beobachtungszeitraumes durchschnittlich anstieg.

<popup name="Hilfestellung"> Differenzenquotient

<popup name="Was genau ist der Differenzenquotient">

</popup>

<popup name="Lösung">(h(8)-h(0))/(8-0)=...=0.16 </popup>

c) Ermittel den Zeitpunkt, zu dem der höchste Wasserstand an der Messtation erreicht wurde. Bereche auch den exakten Höchststand. <popup name="Hilfestellung 1"> Extrempunkt (Hochpunkt) </popup> <popup name="Hilfestellung 2"> Ansatz: hinreichende Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösungen"> Extremstelle liegt bei t= 32/3 (und t=0). Hochpunkt ist H(32/3 | 5771/540). Der Wasserstand liegt bei etwas 10,69 m. </popup>
d) Bestimme den Zeitpunkt, zu dem der Wasserstand am schnellsten anstieg, rechnerisch. <popup name="Hilfestellung 1"> Wendestelle (Extremstelle der 1. Ableitung) </popup> <popup name="Hilfestellung 2"> Ansatz: hinreichende Bedingung h"(t)=0 und h'"(t)≠0 </popup> <popup name="Lösungen"> Wendestelle liegt bei t=16/3. Daraus folgt, dass der Wasserstand nach 5 Stunden und 20 Minuten am schnellsten anstieg. </popup>

Vorlage:Arbeiten
a) Wie viele Besucher hatte die Internetseite um 10 Uhr?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="Lösung"> Es sind 270 Besucher </popup>

b) Wie viele Nutzer sind von 8 bis 10 Uhr im Durchschnitt pro Stunde dazu gekommen?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="Lösung"> Es sind 206 Nutzer pro Stunde </popup>

c) Zu welchem Zeitpunkt hat sich die Bescuherzahl durchschnittlich am stärksten geändert?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="genauere Hilfe"> Die Stelle an der ein Graph die stärkste Änderung (der Steigung) hat, heißt Wendestelle.
Um eine Wendestelle zu berechnen müssen folgende zwei Bedingungen erfüllt sein:
notwendige Bedingun: f´´(t) = 0
hinreichende Bedingung: f´´´(t) ≠ 0 </popup> <popup name="Lösung"> Bei t=10 </popup>

d) Zu welcher Uhrzeit haben die meisten Besucher die Internetseite besucht?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.


<popup name="Lösung"> Bei t = 15 </popup>

Vorlage:Arbeiten
a) Zu welchem Zeitpunkt werden die meisten Karten pro Minute verkauft? <popup name="Hilfestellung 1"> Extrempunkt (Hochpunkt) </popup> <popup name="Hilfestellung 2"> Ansatz: hinreichende Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösung"> Der Hochpunkt liegt bei t=29,933 </popup>
b) Wann im Verlauf der ersten Stunde nimmt die Anzahl der verkauften Karten am schnellsten ab? <popup name="Hilfestellung 1"> Wendestelle (Extremstelle der 1. Ableitung) </popup> <popup name="Hilfestellung 2"> Ansatz: hinreichende Bedingung h"(t)=0 und h'"(t)≠0 </popup> <popup name="Lösung"> Der Wendepunkt liegt bei t=20. </popup>