Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in rechtwinkligen Dreiecken

Startseite (Vorwissen)

1) Sinus, Kosinus, Tangens

2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken

Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken

2.1 Größen in rechtwinkligen Dreiecken berechnen

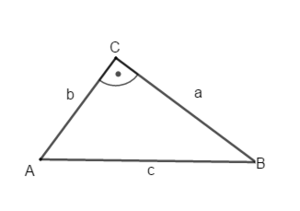
Du kennst schon eine Möglichkeiten, eine fehlende Seitenlänge in einem rechtwinkligen Dreiecken zu berechnen, wenn zwei Seiten gegeben sind:

Erinnerung: Mit dem Satz des Pythagoras!

Wenn nun in einem rechtwinkligen Dreieck eine Seite und ein Winkel gegeben sind, kannst du mithilfe von Sinus, Kosinus und Tangens die Längen der anderen Seiten berechnen.
Wo kannst du das anwenden? Warum sollst du das lernen?
Es hilft z.B. bei Vermessungen:

St. Otger von Westen mit eingerüstetem Turm

Wir haben in Klasse 7 die Höhe des Stadtlohner Kirchturms mithilfe einer maßstabsgetreuen Zeichnung bestimmt, erinnerst du dich? Nun haben wir die Möglichkeit, die Höhe auf eine andere Art zu berechnen.

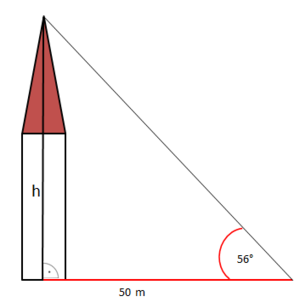
Wir messen den Blickwinkel, unter dem wir die Spitze des Kirchturms sehen und die Entfernung zur Kirche. Welche Größen des rechtwinkligen Dreiecks sind also gegeben, welche Größe ist gesucht?

Im rechtwinkligen Dreieck ist der Winkel $\beta$ = 56° gegeben, der Winkel $\alpha$ ist der rechte Winkel. Außerdem ist die Länge der Seite c = 50 m gegeben. Das ist die Ankathete zu $\beta$.
Gesucht ist die Länge der Seite h. Dies ist die Gegenkathete zu $\beta$.

Also hilft uns hier der Tangens weiter, denn tan $\beta$ = $\tfrac{h}{c}$.

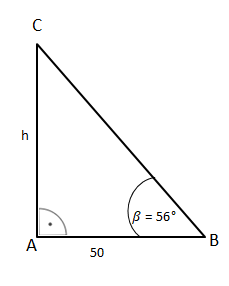
Bestimme nun die Höhe des Kirchturms!

tan $\beta$ = $\tfrac{Gegenkathete}{Ankathete}$ = $\tfrac{h}{50}$. Stelle nun diese Gleichung nach h um.

tan (56°) = $\tfrac{h}{50}$ |∙ 50
tan (56°) ∙ 50 = h
74,1 (m)$\approx$ h

Der Kirchturm ist also ca. 74 m hoch.

Übung 1 (online)

Gib das Seitenverhältnis an und berechne jeweils die Länge der Strecke x in den nachfolgenden LearningApps.

Übung 2 (online und im Heft)

Löse auf der Seite Aufgabenfuchs die folgenden Aufgaben. Notiere zu jeder Aufgabe eine Lösung ausführlich mit Skizze und Rechnung in deinem Heft.

• 8
• 17
• 25

Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken

Sind in einem rechtwinkligen Dreieck zwei Seitenlängen oder eine Seite und ein Winkel gegeben, kannst du fehlenden Größen mithilfe von Sinus, Kosinus und Tangens berechnen.

Wähle das passende Seitenverhältnis aus (Sinus, Kosinus oder Tangens) und stelle - falls nötig - die Formel um.
Übertrage die nachfolgenden Beispiele in dein Heft.

Beispiele:
Beispiel 1: eine Seite (Hypotenuse) und ein Winkel sind gegeben

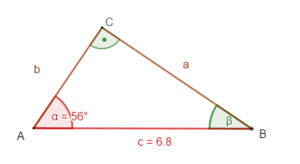
geg: rechtwinkliges Dreieck ($\gamma$ = 90°); c = 6,8 cm; $\alpha$ = 56°
ges: a; b; $\beta$

① Bestimme a:

sin α = $\tfrac{a}{c}$   |∙c
a = sin α ∙ c
a = sin (56°)∙6,8

a $\approx$ 5,6 (cm)

② Bestimme b:

cos α = $\tfrac{b}{c}$   |∙c
b = cos α ∙ c
b = cos (56°)∙6,8

b $\approx$ 3,8 (cm)

③ Bestimme β:

Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
   = 180° - 56° - 90°

   = 34°

Anmerkungen:
Du kannst b auch mit dem Satz des Pythagoras bestimmen:
a² + b² = c² (denn a und b sind die Katheten, c ist die Hypotenuse im rechtwinkligen Dreieck)
b = $\sqrt{\text{c²-a²}}$
   = $\sqrt{\text{6,8²-5,6²}}$
  $\approx$ 3,9 (cm) Der Wert ist ungenauer, da du mit dem gerundeten Wert von a weitergerechnet hast.

Du kannst β auch kürzer bestimmen mit

α + β = 90°, da γ = 90° ist. Ziehst du diese von 180° ab, so bleiben 90° übrig.

Beispiel 2: eine Seite (Kathete) und ein Winkel sind gegeben

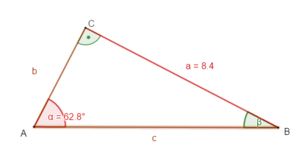
geg: rechtwinkliges Dreieck ($\gamma$ = 90°); a = 8,4 cm; $\alpha$ = 62,8°
ges: b; c; $\beta$

① Bestimme c:

sin α = $\tfrac{a}{c}$   |∙c
c ∙ sin α = a   |: sin α
c = $\tfrac{a}{\text{sin α}}$
c = $\tfrac{8,4}{\text{sin (62,8°)}}$

   $\approx$ 9,4 (cm)

② Bestimme b (mit tan α oder mit dem Satz des Pythagoras):

tan α = $\tfrac{a}{b}$   |∙b
b ∙ tan α = a   |: tan α
b = $\tfrac{a}{\text{tan α}}$
b = $\tfrac{8,4}{\text{tan (62,8°)}}$

   $\approx$ 4,3 (cm)

③ Bestimme β:

Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
   = 180° - 68,2° - 90°

   = 27,2°

Beispiel 3: zwei Seiten sind gegeben (Kathete und Hypotenuse)

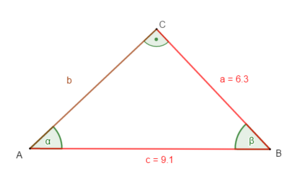
geg: rechtwinkliges Dreieck ($\gamma$ = 90°); a = 6,3 cm; c = 9,1 cm
ges: b; α; β

① Bestimme c (Pythagoras):

a² + b² = c²  |$\surd$
b = $\sqrt{\text{c²-a²}}$
b = $\sqrt{\text{9,1²-6,3²}}$

b $\approx$ 6,6 (cm)

② Bestimme den Winkel α :

sin α = $\tfrac{a}{c}$  
sin α = $\tfrac{6,3}{9,1}$  | sin^-1

$\alpha \approx$ 43,8°

③ Bestimme β:

Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
   = 180° - 43,8° - 90°

   = 46,2°

Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin^-1, cos^-1 bzw. tan^-1 dem Taschenrechner wie die Bilder zeigen:

Beispiel 4: zwei Seiten sind gegeben (beide Katheten)

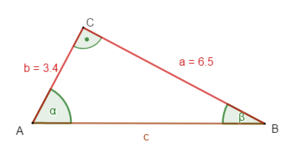
geg: rechtwinkliges Dreieck ($\gamma$ = 90°); a = 6,5 cm; b = 3,4 cm
ges: c; α; β

① Bestimme c (Pythagoras):

a² + b² = c²  |$\surd$
c = $\sqrt{\text{a²-b²}}$
c = $\sqrt{\text{6,8²-3,4²}}$

c $\approx$ 7,3 (cm)

② Bestimme den Winkel α :

tan α = $\tfrac{a}{b}$  
tan α = $\tfrac{6,8}{3,4}$  | tan^-1

$\alpha \approx$ 62,4°

③ Bestimme β:

Winkelsummensatz für Dreiecke:
α + β + γ = 180°
β = 180° - α - γ
   = 180° - 62,4° - 90°

   = 27,6°

Der Wert von Sinus, Kosinus und Tangens ist abhängig vom Winkel α. Jedem Sinuswert, Kosinuswert und Tangenswert ist ein Winkel zugeordnet. Den Winkel berechnest du mit der jeweiligen Umkehrfunktion sin^-1, cos^-1 bzw. tan^-1 dem Taschenrechner wie die Bilder zeigen:

Die Videos fassen die Möglichkeiten der Berechnungen zusammen:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 3

Löse die Aufgaben ausführlich im Heft, nutze die Schreibweisen der Beispiele. Übertrage die Planskizzen aus dem Buch in dein Heft.

• S. 94 Nr. 1
• S. 94 Nr. 2
• S. 94 Nr. 3

a) Löse wie in Beispiel 1
b) Löse wie in Beispiel 2
c) Löse wie in Beispiel 4

d) Löse wie in Beispiel 3

Lösungen (der Größe nach sortiert)
2,9cm; 4,4cm; 5,7cm; 8,1cm; 12,2cm; 14,0cm;

29,7°; 37,7°; 52,3°; 60,3°; 60,5°; 62,6°

a) Löse wie in Beispiel 2
b) Löse wie in Beispiel 3
c) Löse wie in Beispiel 4

d) Löse wie in Beispiel 1

Lösungen (der Größe nach sortiert):
3,8cm; 5,7cm; 6,8cm; 7,8cm; 11,9cm; 14,1cm;

24,4°; 29,2°; 29,5°;57,5°; 60,8°; 65,6°

Löse wie in Beispiel 1

Lösungen:

3,731km; 4,952km

Übung 4

Zeichne zunächst eine Planskizze mit γ = 90° und markiere die gegebenen Größen. Berechne danach die fehlenden Größen. Notiere deine Rechnungen ausführlich. Buch

• S. 95 Nr. 4

a) Löse wie in Beispiel 1.
b) Löse wie in Beispiel 4.
c) Löse wie in Beispiel 3.
d) Löse wie in Beispiel 1.
e) Löse wie in Beispiel 2.
f) Löse wie in Beispiel 2.

2.2 Zusammenhang Steigung m und Steigungswinkel α

Du hast zu Beginn drei Möglichkeiten wiederholt, die Steigung z.B. einer Straße anzugeben.
In Prozent (mit p% = m), als Steigung m und mit dem Steigungswinkel α.
Mithilfe des Tangens kannst du nun zum einer Steigung m den zugehörigen Steigungswinkel α angeben und umgekehrt.

Steigung m = $\frac{\text{Höhenunterschied}}{\text{Horizontalunterschied}}$

m = $\tfrac{a}{b}$ und ebenfalls ist tan α = $\tfrac{a}{b}$, also gilt

m = tan α

Berechne die Steigung m, wenn der Steigungswinkel α gegeben ist:

geg: α = 7°
ges: m
m = tan α
   = tan (7°)
   $\approx$ 0,123

   = 12,3%

Berechne den Steigungswinkel α, wenn die Steigung m gegeben ist.

geg: m = 25% = 0,25
ges: α
tan α = m tan α = 0,25   |tan^-1

 α = 14°

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 5

Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich.

• S. 96 Nr. 12
• S. 96 Nr. 16

HIER WEITERARBEITEN

2.3 Anwendungsaufgaben

Übung 6

Löse die folgenden Aufgaben aus dem Buch. Zeichne zu jeder Aufgabe eine passende Skizze (rechtwinkliges Dreieck) und notiere deine Rechnungen vollständig und übersichtlich.

• S. 96 Nr. 14
• S. 96 Nr. 15
• S. 97 Nr. 17
• S. 97 Nr. 19

Materialsammlung: Übungen auf der Seite Aufgabenfuchs Übungen auf der Seite mathe-trainer