Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 38: | Zeile 38: | ||
Dieses Verhältnis wird '''Kreiszahl π''' genannt. <math>\tfrac{u}{d}</math> = π = 3,141... Dieser Dezimalbruch endet nie.<br> | Dieses Verhältnis wird '''Kreiszahl π''' genannt. <math>\tfrac{u}{d}</math> = π = 3,141... Dieser Dezimalbruch endet nie.<br> | ||
[[Datei:Football-157930 1280.png|rechts|rahmenlos]]Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden: Beeindruckend! | [[Datei:Football-157930 1280.png|rechts|rahmenlos|100.99x100.99px]]Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden: Beeindruckend! | ||
{{#ev:youtube|KIZOpIcBEnI|800|center}}<br> | {{#ev:youtube|KIZOpIcBEnI|800|center}}<br> | ||
| Zeile 45: | Zeile 45: | ||
Applet von Pöchtrager<br> | Applet von Pöchtrager<br> | ||
[[Datei:Pi-3166190 1920.png|rechts|rahmenlos]] Und nun noch einige kurze Infos zur Kreiszahl π: | [[Datei:Pi-3166190 1920.png|rechts|rahmenlos|200.99x200.99px]] Und nun noch einige kurze Infos zur Kreiszahl π: | ||
* eine der bekanntesten und sagenumwobensten Zahlen der Mathematik | |||
* Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet | *eine der bekanntesten und sagenumwobensten Zahlen der Mathematik | ||
* mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14) | *Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet | ||
* Mittlerweile (2010) von dem Mathematiker Shigero Kondo auf ca. 5 000 000 000 000 Dezimalstellen berechnet | *mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14) | ||
* beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist: | *Mittlerweile (2010) von dem Mathematiker Shigero Kondo auf ca. 5 000 000 000 000 Dezimalstellen berechnet | ||
*beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist: | |||
[[Datei:Unfolding circle demonstration of pi.gif|ohne|mini]] | [[Datei:Unfolding circle demonstration of pi.gif|ohne|mini]] | ||
π = <math>\tfrac{u}{d}</math> = 3,14159... | π = <math>\tfrac{u}{d}</math> = 3,14159... | ||
*Ein Kreis mit dem Durchmesser 1 hat somit einen Umfang von π. | |||
=== 1.3 Kreisumfang - Berechnungen === | ===1.3 Kreisumfang - Berechnungen=== | ||
Version vom 7. April 2021, 10:51 Uhr
SEITE IM AUFBAU!!
1 Kreisumfang
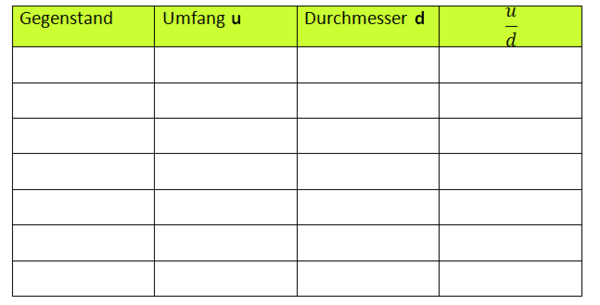
1.1 Kreisumfang entdecken
Prüfe deine Vermutung aus dem Teil c) mithilfe des nachfolgenden Applets. Wähle den Vollbildmodus zur Bearbeitung.
Applet von Pöchtrager
Der Umfang u eines Kreises ist proportional zu seinem Durchmesser d.
Der Quotient beträgt immer ca. 3,1.
Zusammenfassung:
1.2 Exkurs: Kreiszahl π
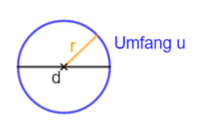
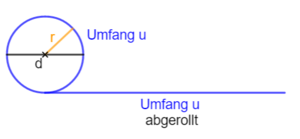
Beim Kreis ist das Verhältnis von Umfang u und Durchmesser d ist immer gleich.
Dieses Verhältnis wird Kreiszahl π genannt. = π = 3,141... Dieser Dezimalbruch endet nie.
Dorfuchs hat die ersten 200 Nachkommastellen von π mit einer Fußballjonglage verbunden: Beeindruckend!
Das folgende Näherungsverfahren für die Kreiszahl π geht auf Archimedes (282 v.Chr. Bis 212 v.Chr.) zurück. Es beruht auf der Betrachtung von regelmäßigen Vielecken, die dem Kreis umschrieben bzw. einbeschrieben sind.

Applet von Pöchtrager
Und nun noch einige kurze Infos zur Kreiszahl π:
- eine der bekanntesten und sagenumwobensten Zahlen der Mathematik
- Ansätze ihrer Berechnung wurden schon im 17 Jahrhundert v. Chr. im Rechenbuch des Ahmes angedeutet
- mathematisch relativ genau als erstes von dem griechischen Mathematiker und Philosoph Archimedes im Jahr 250 v .Chr. bestimmt worden, mit 2 Dezimalstellen (3,14)
- Mittlerweile (2010) von dem Mathematiker Shigero Kondo auf ca. 5 000 000 000 000 Dezimalstellen berechnet
- beschreibt das Verhältnis vom Umfang des Kreise zu seinem Durchmesser, welches bei allen Kreisen gleich ist:
π = = 3,14159...
- Ein Kreis mit dem Durchmesser 1 hat somit einen Umfang von π.
1.3 Kreisumfang - Berechnungen
{{Box|Übung 3 - geometrische Anwendungen|
- S. 129 Nr. 4
- S. 129 Nr. 5