Benutzer:Buss-Haskert/Kreis und Zylinder/Kreisumfang: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 6: | Zeile 6: | ||
<br> | <br> | ||
==1 Kreisumfang== | ==1 Kreisumfang== | ||
=== 1.1 Kreisumfang entdecken === | |||
{{Box|Kreisumfang entdecken|Was ist größer? Die Höhe oder der Umfang des Glases?<br> | {{Box|Kreisumfang entdecken|Was ist größer? Die Höhe oder der Umfang des Glases?<br> | ||
Schau in der folgenden LearningApp das Video dazu an.|Unterrichtsidee}} | Schau in der folgenden LearningApp das Video dazu an.|Unterrichtsidee}} | ||
| Zeile 27: | Zeile 28: | ||
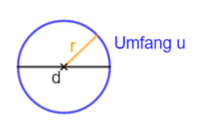
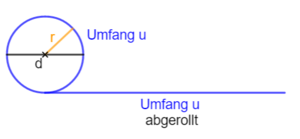
{{Box|1=Kreisumfang|2=[[Datei:Kreisumfang 1.png|rechts|rahmenlos|200px]][[Datei:Kreisumfang 2.png|rechts|rahmenlos]]Den '''<u>Umfang u</u>''' eines Kreises mit Durchmesser d (Radius r)<br> berechnen wir mit der Formel:<br><br> | {{Box|1=Kreisumfang|2=[[Datei:Kreisumfang 1.png|rechts|rahmenlos|200px]][[Datei:Kreisumfang 2.png|rechts|rahmenlos]]Den '''<u>Umfang u</u>''' eines Kreises mit Durchmesser d (Radius r)<br> berechnen wir mit der Formel:<br><br> | ||
<big>u = π · d oder u = 2· π · r </big> (denn d = 2·r)|3=Arbeitsmethode}} | <big>u = π · d oder u = 2· π · r </big> (denn d = 2·r)|3=Arbeitsmethode}} | ||
=== 1.2 Exkurs: Kreiszahl π === | |||
{{Box|Übung 1 - online|Löse auf der Seite [https://www.aufgabenfuchs.de/mathematik/flaeche/kreis/kreis.shtml '''Aufgabenfuchs'''] die Aufgaben | |||
* 5 | |||
* 6 | |||
* 7 | |||
* 8|Üben}} | |||
{{Box|Übung 2 - Grundlagen|Löse die Aufgaben aus dem Buch. Notiere übersichtlich mit den Schreibweisen wie in den Beispielen. | |||
* S. 129 Nr. 1 (Wähle je eine Aufgabe aus a-c und eine Aufgabe aus d-e aus.) | |||
* S. 129 Nr. 2 (Wähle eine Aufgabe aus.) | |||
* S. 129 Nr. 3 (Wähle drei Aufgaben aus.)|Üben}} | |||
{{Box|Übung 3 - geometrische Anwendungen| | |||
* S. 129 Nr. 4 | |||
* S. 129 Nr. 5 | |||
Version vom 7. April 2021, 08:25 Uhr
SEITE IM AUFBAU!!
1 Kreisumfang
1.1 Kreisumfang entdecken
Prüfe deine Vermutung aus dem Teil c) mithilfe des nachfolgenden Applets. Wähle den Vollbildmodus zur Bearbeitung.
Applet von Pöchtrager
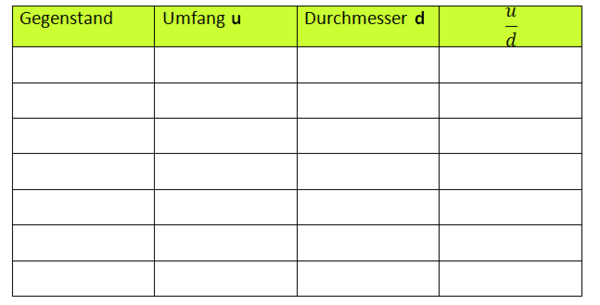
Stelle deine Werte aus der Tabelle in einem d-u-Diagramm dar. Was fällt dir auf?
Das Diagramm ist eine Ursprungsgerade, also ist die Zuordnung proportional. Das heißt auch, dass der Quotient immer gleich ist.
Der Umfang u eines Kreises ist proportional zu seinem Durchmesser d.
Der Quotient beträgt immer ca. 3,1.
1.2 Exkurs: Kreiszahl π
{{Box|Übung 3 - geometrische Anwendungen|
- S. 129 Nr. 4
- S. 129 Nr. 5