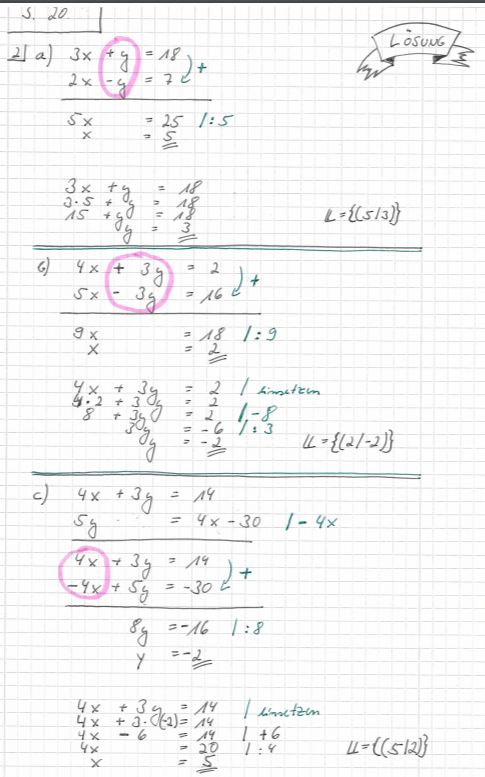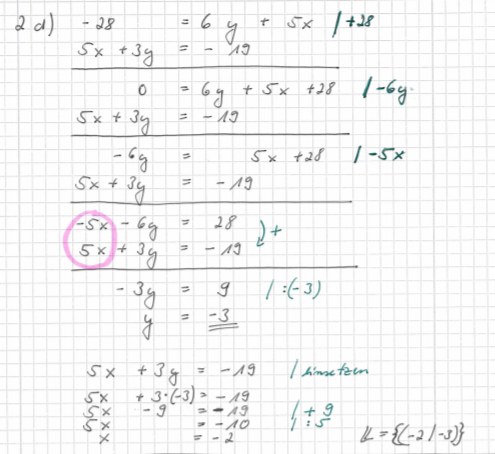Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme rechnerisch lösen
1) Lineare Gleichungen mit zwei Variablen
2) Lineare Gleichungssysteme
3) Lineare Gleichungssysteme zeichnerisch lösen
4) Lineare Gleichungssysteme rechnerisch lösen
5) Modellieren
6) Checkliste
4) Lineare Gleichungssysteme rechnerisch lösen
- Die Zeichnungen der Geraden können ungenau sein.
- Der Schnittpunkt kann ungenau abgelesen werden, wenn er keine ganzzahligen Koordinaten hat.
- Die Skala muss teilweise sehr groß gewählt werden, daher können die Koordinaten des Schnittpunktes nur ungenau abgelesen werden.
Daher wirst du nun verschiedene rechnerische Verfahren kennenlernen!
4.1) Das Gleichsetzungsverfahren
Du kannst das Problem durch Probieren lösen. Als Darstellung bietet sich hier eine Tabelle an:
| Anzahl der Hasen | Anzahl der Hühner | Anzahl der Tiere | Anzahl der Beine |
| 1 | 9 | 10 | 1·4+9·2=22<28 |
| 2 | 8 | 10 | ... |
| ... | ... | 10 | ... |
x=Anzahl der Hasen; y=Anzahl der Hühner
Nun kannst du zwei Gleichungen aufstellen: Eine Gleichung für die Anzahl der Tiere und die andere Gleichung für die Anzahl der Beine, wobei jeder Hase ja vier Beine hat und jedes Huhn zwei.
Wenn wir die Bedeutung der Variablen mit x = Anzahl der Hasen und y = Anzahl der Hühner festlegen, ergeben sich die folgenden Gleichungen:
I. x + y = 10
II. 4x + 2y = 28
Formen wir nun beide Gleichungen nach y um, ergibt sich:
I. y = -x + 10
II. y = -2x + 14
Nun haben wir eine Darstellung, bei der links in beiden Gleichungen y isoliert steht.
Einmal soll y = -x + 10 sein und außerdem y = -2x + 14. Die zugehörigen Terme auf der rechten Seite haben also auch den gleichen Wert und deshalb können wir sie gleichsetzen:
-x + 10 = -2x + 14
Diese neue Gleichung hat nur noch eine Variable, nämlich x, und wir können die Gleichung nach x auflösen.
-x + 10 = -2x + 14 |+2x
x + 10 = 14 |-10
x = 4
Da x für die Anzahl der Hasen steht, gibt es also 4 Hasen. Um die Anzahl der Hühner herauszufinden, setzen wir in eine der beiden Ausgangsgleichungen für x die Zahl 4 ein und lösen diese dann nach y auf:
x = 4 in I.: 4 + y = 10 |-4
y = 6
Also gibt es 6 Hühner im Stall und 4 Hasen.
Wir können unsere Lösung prüfen, indem wir x = 4 und y = 6 in die Ausgangsgleichungen einsetzen. Ist unsere Lösung richtig, müssen sich wahre (w) Aussagen ergeben:
I. 4 + 6 = 10 und II. 4 ∙ 4 + 2 ∙ 6 = 28
10 = 10 (w) und 28 = 28 (w).
Also gibt es 4 Hasen und 6 Hühner im Stall.
[Du kannst diese Lösung auch mit GeoGebra prüfen. Der Schnittpunkt der Graphen ist S(4|6).]
Die Videos erklären das Gleichsetzungsverfahren noch einmal:

a) Löse nach x auf.
b) Löse nach y auf.
c) Löse nach y auf.
d) Löse nach 3x auf.
Vereinfache zuerst die Gleichungen:
I 3x+4y-5 = 2x+3y-1 |-2x;-3y;+5
I´ x+y=4
II´ 2x+y=3
Jetzt siehst du, dass es vorteilhaft ist, die Gleichungen nach y aufzulösen und dann wie gewohnt weiterzuarbeiten.
Du kannst deine Ergebnisse immer mit GeoGebra prüfen. Du kannst dort einfach die Ausgangsgleichungen einsetzen, das Programm stellt die Gleichungen dann so um, dass es die Graphen zeichnen kann. Der Schnittpunkt der Geraden ist die Lösung des LGS.
x = erste Zahl; y=zweite Zahl
Falls du Schwierigkeiten mit den Fachbegriffen hast, löse die folgenden Quizze.
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
4.2) Das Additionsverfahren
x=Jans Alter; y=Toms Alter
Nun kannst du zwei Gleichungen aufstellen: Eine Gleichung für das Alter zusammen und eine Gleichung für den Altersunterschied.
Wenn wir die Bedeutung der Variablen mit x=Jans Alter und y= Toms Alter festlegen, ergeben sich die folgenden Gleichungen:
I. x + y = 24
II. x - y = 2
Es fällt auf, dass in Gleichung I. ... +y gerechnet wird und in Gleichung II. ... -y . Daher bietet es sich an, beide Gleichungen zu addieren:
I. + II.
I. x + y = 24
II. x - y = 2 |addiere beide Gleichungen also x + x + y - y = 24 + 2
2x + 0 = 26
Diese neue Gleichung hat nur noch eine Variable, nämlich x, und wir können die Gleichung nach x auflösen.
2x = 26 |: 2
x = 13
Da x für das Alter von Jan steht, ist Jan also 13 Jahre alt. Um das Alter von Tom herauszufinden, setzen wir in eine der beiden Gleichungen für x die Zahl 13 ein und lösen diese dann nach y auf:
x=13 in I.: 13 + y = 24 |-13
y = 11
Also ist Tom 11 Jahre alt und Jan 13.
Wir können unsere Lösung prüfen, indem wir x=13 und y=11 in die Ausgangsgleichungen einsetzen. Ist unsere Lösung richtig, müssen sich wahre (w) Aussagen ergeben:
I. 13 + 11 = 24 und II. 13 - 11 = 2
24 = 24 (w) und 2 = 2 (w).
Also ist Jan 13 Jahre alt und Tom 11.
(Du kannst diese Lösung auch mit GeoGebra prüfen. Der Schnittpunkt der Graphen ist S(13|11).)
Die Videos erklären das Additionsverfahren noch einmal:
und für Fans von Lehrer Schmidt (jetzt wird es komplizierter):
Es ist nicht immer y, das beim Addieren wegfällt. Sortiere zunächst die Gleichungen so: ...x...y = ... Forme dann hier Gleichung II so um, dass du -4x rechnest. Dann fällt beim Addieren die Variable x weg. Die Probe erfolgt dann wie immer (rechnerisch und/oder mit GeoGebra).
I. 4x + 3y = 35
II. 5y = 4x - 30 |-4x
I. 4x + 3y = 35
II.-4x + 5y = -30
b) Multipliziere II mit 3.
c)Multipliziere II mit 2.
d) Multipliziere I mit 2.
a) Multipliziere Gleichung I mit 3 und Gleichung II mit 2. Du erhältst I. 15x+6y=48 und II. 16x-6y=14. Nun addiere I und II.
b) Multipliziere Gleichung I mit 2 und Gleichung II mit 5
c) Multipliziere Gleichung I mit 3 und Gleichung II mit 2.
d) Multipliziere Gleichung I mit 4 und Gleichung II mit 3
4.3) Das Einsetzungsverfahren
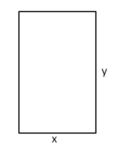
Lege die Bedeutung der Variablen fest und beschrifte die Skizze.
x=Länge; y=Breite
Nun kannst du zwei Gleichungen aufstellen: Eine Gleichung für den Umfang ("Kalle läuft") und die andere Gleichung für die Breite.
Wenn wir die Bedeutung der Variablen mit x=Länge und y=Breite festlegen, ergeben sich die folgenden Gleichungen:
I. 2x + 2y = 44 (Umfang: "Kalle läuft" um das Rechteck herum)
II. y = x+6 (Die Breite ist um 6cm länger als die Länge)
Nun siehst du, dass Gleichung II. schon nach y aufgelöst ist:
I. 2x + 2y = 44
II. y = x+6
Das bedeutet, dass du überall statt y auch x+6 schreiben kannst, denn diese Terme sind gleich!
Daher kannst du in Gleichung I. statt y den Term x+6 einsetzen:
2x + 2·(x+6) = 44
Diese neue Gleichung hat nur noch eine Variable, nämlich x, und wir können die Gleichung nach x auflösen.
2x + 2·(x+6) = 44 |ausmultiplizieren ("Jedem die Hand geben")
2x + 2x + 12 = 44 | gleichartige Terme zusammenfassen
4x + 12 = 44 |-12
4x = 32 |:4
x = 8
Da x für die Länge des Rechtecks steht, ist dieses also 8 cm lang. Um die Breite herauszufinden, setzen wir in die zweite Gleichung für x die Zahl 8 ein und lösen diese dann nach y auf:
x=8 in II.: y = 8 + 6
y = 14
Das Rechteck ist also 8 cm lang und 14 cm breit.
Wir können unsere Lösung prüfen, indem wir x=8 und y=14 in die Ausgangsgleichungen einsetzen. Ist unsere Lösung richtig, müssen sich wahre (w) Aussagen ergeben:
I. 2·8 + 2·14 = 44 und II. 14 = 8 + 6
16 + 28 = 44 und 14 = 14 (w).
44 = 44 (w) und 14 = 14 (w).
Das Rechteck ist 8cm lang und 14cm breit.
(Du kannst diese Lösung auch mit GeoGebra prüfen. Der Schnittpunkt der Graphen ist S(8|14).)
Die Videos erklären das Einsetzungsverfahren noch einmal:
Zusammenfassung - Übersicht
Prüfe deine Lösung jeweils mit Geogebra