Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen

Info

In diesem Lernpfadkapitel lernst du

• wie du von Pyramiden den Oberflächeninhalt schätzen kannst.
• wie du von Pyramiden den Oberflächeninhalt berechnen kannst.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Wiederholung

Info

Um die Oberfläche einer Pyramide zu bestimmen, ist es wichtig, dass du weißt, wie man den Flächeninhalt von Rechtecken und von Dreiecken bestimmt. Wenn du dich noch daran erinnerst, wie man diesen bestimmt, kannst du direkt zu Aufgabe 5 gehen. Wenn du dir noch etwas unsicher bist und eine kurze Wiederholung brauchst, bearbeite die folgenden Aufgaben (Aufgaben 1, 2, 3 und 4).

Rechteckigen Flächeninhalt berechnen

Aufgabe 1: Flächeninhalt vom Rechteck

Berechne den Flächeninhalt des folgenden Quadrates (denke auch daran, die richtige Einheit anzugeben):

Zur Berechnung des Flächeninhaltes benötigst du nicht die Diagonale.

Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: $A=a \cdot b$

$A=4 \text{ cm} \cdot 3 \text{ cm} =12 \text{ cm}^{2}$

Dreieckigen Flächeninhalt berechnen

Aufgabe 2: Flächeninhalt vom Dreieck

Berechne den Flächeninhalt des folgenden Dreiecks (denke auch daran, die richtige Einheit anzugeben):

Du benötigst zur Berechnung eines dreieckigen Flächeninhaltes die Höhe und die Grundseite.

Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: $A=\tfrac{g \cdot h}{2}$

$A= \tfrac{4 \text{ cm} \cdot 6 \text{ cm}}{2} =12 \text{ cm}^{2}$

Info

In den Aufgaben 3 und 4 hast du noch einmal die Möglichkeit, das Bestimmen von recht- und dreieckigen Flächeninhalten zu üben. Solltest du dich schon sicher fühlen, kannst du auch direkt mit Aufgabe 5 weitermachen.

Aufgabe 3: Rechteckige Flächeninhalte

Berechne den Flächeninhalt folgender Rechtecke.

a) $a=7\text{ m}, b=5\text{ m}$

$A=7 \text{ m} \cdot 5 \text{ m} =35 \text{ m}^{2}$

b) $a=90\text{ dm}, b=2\text{ m}$

Berechnung in m: $A=9 \text{ m} \cdot 2 \text{ m} =18 \text{ m}^{2}$

oder

Berechnung in dm: $A=90 \text{ dm} \cdot 20 \text{ dm} =1800\text{ dm}^{2}$

Aufgabe 4: Dreieckige Flächeninhalte

Berechne den Flächeninhalt folgender Dreiecke.

a) $g=16\text{ m}, h=7\text{ m}$

$A=56\text{ m}^{2}$

b) $g=4\text{ m}, h=500\text{ cm}$

$A=10\text{ m}^{2}, A=1000\text{ dm}^{2}, A=100000\text{ cm}^{2}$

Aufgabe 5: Formeln notieren

Kehre nun zum Arbeitsblatt zurück und trage die Formeln zur Berechnung rechteckiger und dreieckiger Flächeninhalte ein.

Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: $A=a \cdot b$

Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: $A=\tfrac{g \cdot h}{2}$

Oberflächeninhalte berechnen

Aufgabe 6: Materialien berechnen

a) Lies dir eine der folgenden Situationsbeschreibungen durch.

1981 initiierte der damalige französische Staatspräsident das Projekt „Grand-Louvre“. Im Rahmen dessen wurde der Architekt Ieoh Ming Pei beauftragt, die heutige Glaspyramide im Zentrum des Palastes zu entwickeln. Die Blaupause steht und die Vision ist klar: Die Pyramide soll komplett mit Glas umfasst werden! Nun geht es darum zu ermitteln, wie viele der rautenförmigen Glasscheiben hergestellt werden müssen.

Die Cheops-Pyramide ist die älteste und größte der drei Pyramiden von Gizeh und wird deshalb auch als „Große Pyramide“ bezeichnet. Diese höchste Pyramide der Welt wurde als Grabmal für den Pharao Cheops etwa 2620 v. Chr. errichtet und gilt heutzutage als eines der sieben Weltwunder der Antike. Natürlich mussten ausreichend Steine gehauen werden, um den Bau zu vollenden. Der zuständige Untertan stand vor der Aufgabe, die passende Anzahl zu berechnen.

Im Zweiten Weltkrieg wurde der St.-Paulus-Dom in Münster durch Bombentreffer schwer beschädigt. In den Jahren 1946 bis 1956 wurde der Dom wieder aufgebaut. Unter anderem mussten die pyramidenförmigen Kirchturmdächer wieder mit neuen Dachziegeln belegt werden, doch die Materialien in der Nachkriegszeit waren knapp. Somit soll eine möglichst passende Anzahl berechnet werden.

 

b) Überlege dir bei einer der Situationen, wie man das Problem mathematisch lösen könnte. Beschreibe dein Vorgehen auf einem Zettel in Stichpunkten. Hier sind keine Rechnungen erforderlich und du brauchst auch nicht zählen.

Die Gebäude sind allesamt Pyramiden und haben vier gleichgroße, dreieckige Seitenflächen. Was benötigst du zum Berechnen einer solchen Seitenfläche? Muss die Grundfläche bei der Materialberechnung berücksichtigt werden?

Da die Pyramiden auf einem Untergrund stehen, muss die Grundfläche nicht berechnet werden.

Da eine Seitenfläche dreieckig ist, kann man die Formel zur Berechnung eines Dreiecks benutzen:

$A = \frac{g \cdot h_g}{2}$

Da die Seitenflächen gleichgroß sind, braucht man nur den Materialverbrauch für eine Seitenfläche zu berechnen und vervierfacht diesen.

$4 \cdot A = 4 \cdot \frac{g \cdot h_g}{2} = 2 \cdot g \cdot h_g$

Man benötigt also nur die Maße der Grundseite und der Höhe des Dreiecks, um den Flächeninhalt einer Seitenfläche zu bestimmen. Wenn man nun den Flächeninhalt kennt, den ein Materialstück benötigt, so kann man durch Teilen den Materialverbrauch für eine Seitenfläche berechnen.

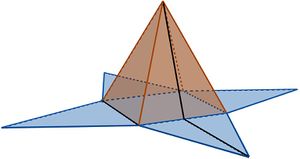
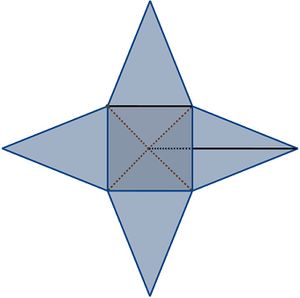
Wie du bereits im vorherigen Kapitel entdeckt hast, lässt sich die Oberfläche einer Pyramide in ein Netz überführen, indem man die Pyramide aufklappt und die Seitenflächen auf eine Ebene faltet.

Das so entstandene Netz besteht somit aus einer Grundfläche $G$ und den dreieckigen Seitenflächen, welche zusammen die sogenannte Mantelfläche $M$ bilden.

Den Flächeninhalt des gesamten Netzes nennt man den Oberflächeninhalt $O$. Du kannst dir diese Größe als Menge an Verpackung vorstellen, die du benötigst, um das pyramidenförmige Objekt zu umschließen.

Merksatz: Oberflächeninhalt

Der Oberflächeninhalt einer Pyramide lässt sich durch die Summe ihrer Grundfläche und ihrer Mantelfläche berechnen. Als Formel ergibt sich somit:

$O = G + M$.

Die Mantelfläche besteht aus mehreren dreieckigen Seitenflächen. Die Anzahl dieser Seitenflächen ist gleich der Anzahl der Ecken der Grundfläche.

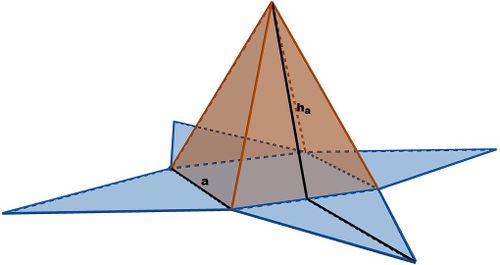
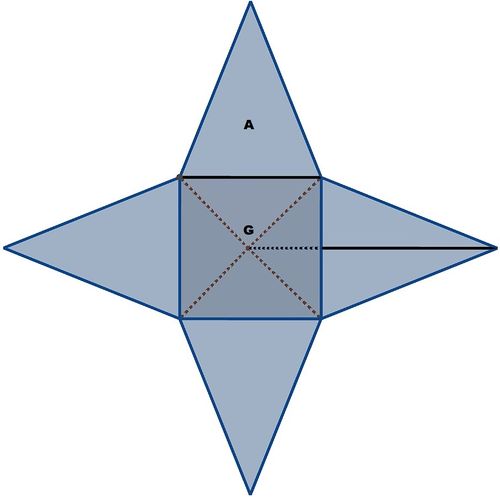
Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken.

Beispiel: Quadratischen Oberflächeninhalt berechnen

Betrachte die Pyramide rechts, mit einer Kantenlänge von $a = 5\text{ cm}$ und einer Seitenhöhe von $h_a = 6\text{ cm}$.

Grundfläche $G$:

$G = a \cdot a$

$G = 5 \cdot 5 = 25$

$G = 25 \text{ cm}^2$.

Seitenfläche $A$:

$A = \frac{a\cdot h_a}{2}$

$A = \frac{5 \cdot 6}{2} = 15$

$A = 15\text{ cm}^2$

Mantelfläche $M$:

$M = 4 \cdot A$

$M = 4 \cdot 15 = 60$

$M = 60\text{ cm}^2$.

Oberflächeninhalt $O$:

$O = G + M$

$O = 25 + 60 = 85$

$O = 85\text{ cm}^2$

Aufgabe 7: Lückentext 'Rechteckige Pyramide'

Aufgabe 8: Oberflächeninhalte verschiedener Pyramiden berechnen

Kehre nun zum Arbeitsblatt zurück und bearbeite die Aufgabe 8 zum Einüben des Verfahrens.

a)

Grundfläche $G$:

$G = a^2$

$G = 6^2 = 36$

Seitenfläche $A$:

$A = \frac{a \cdot h_a}{2}$

$A = \frac{6 \cdot 7}{2} = 21$

Oberflächeninhalt $O$:

$O = G + 4 \cdot A$

$O = 36 + 4 \cdot 21 = 120$

b)

Seitenfläche $A_a$:

$A_a = \frac{a \cdot h_a}{2}$

$A_a = \frac{8 \cdot 6,71}{2} = 26,84$

Seitenfläche $A_b$:

$A_b = \frac{b \cdot h_b}{2}$

$A_b = \frac{6 \cdot 7,21}{2} = 21,63$

Mantelfläche $M$:

$M = 2 \cdot A_a + 2 \cdot A_b$

$M = 2 \cdot 26,84 + 2 \cdot 21,63$

$M = 96,94$

c)

Grundfläche $G$:

$G = a \cdot b$

$G = 6 \cdot 10 = 60$

Seitenfläche $A_a$:

$A_a = \frac{a \cdot h_a}{2}$

$A_a = \frac{6 \cdot 8,6}{2} = 25,8$

Seitenfläche $A_b$:

$A_b = \frac{b \cdot h_b}{2}$

$A_b = \frac{10 \cdot 7,62}{2} = 38,1$

Mantelfläche $M$:

$M = 2 \cdot A_a + 2 \cdot A_b$

$M = 2 \cdot 25,8 + 2 \cdot 38,1$

$M = 127,8$

Oberflächeninhalt $O$:

$O = G + M$

$O = 60 + 127,8 = 187,8$

d)

Seitenfläche $A$:

$A = \frac{a \cdot h_a}{2}$

$A = \frac{2 \cdot 4,72}{2} = 4,72$

Mantelfläche $M$:

$M = 6 \cdot A$

$M = 6 \cdot 4,72 = 28,32$

 

Aufgabe 9: Tetraeder?

Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen.

Du kannst durch Klicken, Ziehen und Loslassen mit der Maus die Pyramide drehen. Außerdem kannst du auch die Zahlen genauso verschieben, um sie besser lesen zu können.

Kevin erwidert, dass dies ja viel zu viel Arbeit sei, da man doch nur eine der Seitenflächen benötigt. Schnell berechnet er:

$O = G + 3 \cdot A = \frac{1}{2} \cdot 6,4 \cdot 3,12 + 3 \cdot \frac{1}{2} \cdot 6,4 \cdot 6 = 67,584$.

Stimmst du diesem Ergebnis zu oder war Kevin doch etwas zu voreilig? Erkläre, welche Fehler Kevin gemacht hat und korrigiere das Ergebnis!

Tatsächlich unterscheiden sich bei dieser Pyramide die Kantenlängen, da es sich nicht um ein gleichseitiges Dreieck als Grundfläche handelt. Somit sind auch die Seitenflächen nicht deckungsgleich und müssen einzeln berechnet werden. Außerdem hat Kevin die Höhe der Pyramide als Seitenhöhe aufgefasst. Eine korrekte Lösung könnte so aussehen:

Grundfläche G:

$G = \frac{1}{2} \cdot g \cdot h_g$

$G = \frac{1}{2} \cdot 6,4 \cdot 3,12$

$G = 9,984$

Mantelfläche M:

$M = A_a + A_b + A_c$

$M = \frac{1}{2} \cdot a \cdot h_a + \frac{1}{2} \cdot b \cdot h_b + \frac{1}{2} \cdot c \cdot h_c$

$M = \frac{1}{2} \cdot 6,4 \cdot 6,09 + \frac{1}{2} \cdot 5 \cdot 6,15 + \frac{1}{2} \cdot 4 \cdot 6,23$

$M = 19,488 + 15,375 + 12,46$

$M = 47,323$

Oberflächeninhalt O:

$O = G + M$

$O = 9,984 + 47,323$

$O = 57,307$

Pyramiden schätzen

Info

Im Alltag kommt es manchmal vor, dass man nicht alle Angaben kennt, die man zur Bestimmung der Oberfläche benötigt. In diesem Abschnitt kannst du deshalb üben, einzelne Angaben oder auch den gesamten Flächeninhalt zu schätzen. Dabei kommt es nicht so sehr darauf an, dass du immer komplett richtig schätzt (das wäre ja auch so gut wie unmöglich), sondern, dass du ein Gefühl für die Größen entwickelst.

Aufgabe 10: Oberfläche von Pyramiden schätzen

Ordne jedem Bild durch Schätzen den passenden Oberflächeninhalt zu (du musst hier nichts rechnen!). Am Ende bleiben einige Werte übrig, da es mehr Werte als Bilder gibt.

Durch Anklicken der Bilder werden diese größer.

Sortiere die Größen erstmal grob bevor du sie den Bildern zuordnest.

Aufgabe 11: Karlsruher Pyramide schätzen

Karlsruher Pyramide

Auf dem Bild siehst du die Karlsruher Pyramide, die auf dem Marktplatz in Karlsruhe steht. Berechne den Oberflächeninhalt (inklusive der Grundfläche), indem du...

a) ... die für die Berechnung notwendigen Größen schätzt,

b) ... anschließend die Fläche mit deinen geschätzten Werten berechnest.

Info

Die Grundfläche der Pyramide kann als quadratisch angenommen werden.

Nutze die Personen auf dem Bild als Referenzgröße.

Info

In der Lösung werden die exakten Werte genutzt, deine Ergebnisse können also etwas von dieser Lösung abweichen. Die Lösung kann dir aber als Orientierung dienen.

Es gilt $h_a=7{,}45 \text{ m}$ und $a=6{,}05 \text{ m.}$

Damit gilt dann:

Grundfläche G:

$G=a^{2}=6{,}05^{2}$

$G=36{,}6 \text{ m}^{2}$

Seitenfläche A:

$A=\frac{a\cdot h_a}{2}=\frac{6{,}05\cdot 7{,}45}{2}$

$A=22{,}54 \text{ m}^{2}$

Mantelfläche M:

$M = 4 \cdot A = 4\cdot 22{,}54$

$M = 90{,}16 \text{ m}^{2}$

Oberfläche O:

$O = G + M = 36{,}6 + 90{,}16$

$O = 126{,}76 \text{ m}^{2}$

Vertiefen und Vernetzen

Info

In diesem Abschnitt findest du vertiefende Aufgaben zu dem Oberflächeninhalt von Pyramiden und darüber hinausgehenden Themen. Neben Pyramiden kommen in diesem Abschnitt auch weitere Körper bzw. Flächen vor, die du zum Teil bereits aus dem Unterricht kennst. Die Aufgabe 13 ist als Knobelaufgabe gedacht, sodass du hier testen kannst, wie fit du im Umgang mit den Oberflächeninhalten von Pyramiden und ähnlichen Körpern bist.

Aufgabe 12: Zusammengesetzte Körper

Kehre zum Arbeitsblatt zurück und bearbeite dort die Aufgabe 12.

Die Dachfläche besteht aus vier Dreiecken, von denen die jeweils gegenüberliegenden gleich groß sind.

Wir berechnen als erstes den Oberflächeninhalt des Quaders. Die Grundfläche berechnet sich aus

$G=a \cdot b=6 \cdot 12=72 \text{ cm}^{2}$.

Als nächstes wird die Mantelfläche des Quaders berechnet.

$M_{\text{Quader}}=2 \cdot a \cdot c+2 \cdot b \cdot c=2 \cdot 6 \cdot 5+2 \cdot 12 \cdot 5=60+120=180 \text{ cm}^{2}$

Nun berechnen wir die Mantelfläche des Daches. Zunächst berechnen wir die Fläche eines der ersten beiden Dreiecke:

$A_{\text{Dreieck-1}}= \frac{1}{2} \cdot a \cdot h_a=\frac{1}{2} \cdot 6 \cdot 8{,}37=25{,}11 \text{ cm}^{2}$.

Nun fehlt noch die Fläche eines der zweiten beiden Dreiecke:

$A_{\text{Dreieck-2}}= \frac{1}{2} \cdot h \cdot h_b=\frac{1}{2} \cdot 12 \cdot 5{,}83=34,98 \text{ cm}^{2}$.

Wir erhalten insgesamt für die Mantelfläche des pyramidenförmigen Daches:

$M_{\text{Dach}}=2 \cdot A_{\text{Dreieck-1}}+2 \cdot A_{\text{Dreieck-2}}=2 \cdot 25{,}11+2 \cdot 34{,}98=50{,}22+69{,}96=120{,}18 \text{ cm}^{2}$.

Insgesamt erhalten wir also: $O=G+M_{\text{Quader}}+M_{\text{Dach}}=72+180+120{,}18=372{,}18 \text{ cm}^{2}$.

Für 23 Schülerinnen und Schüler muss die Lehrkraft also $23 \cdot 372{,}18=8560{,}14 \text{ cm}^{2}$ Papier mitbringen.

Aufgabe 13: Tipi

Tipi

Für das Tipi auf dem Foto soll eine Plane hergestellt werden. Zur Vereinfachung kannst du annehmen, dass das Tipi die Form einer regelmäßigen neuneckigen Pyramide hat, die an einer der Seitenflächen eine halbrunden Öffnung enthält. Der Boden des Tipis wird nicht mit einer Plane ausgekleidet.

Berechne, wie viel Quadratmeter Zeltplane für das Tipi benötigt wird.

Schätze die benötigten Größen zur Berechnung der Fläche, indem du den abgebildeten Menschen als Referenzgröße verwendest.

Der gesuchte Flächeninhalt berechnet sich aus der Mantelfläche abzüglich des halbrunden Eingangs.

Bei dem Eingang handelt es sich um einen Halbkreis. Der Flächeninhalt dieses Halbkreises lässt sich mit der Formel $A=\frac{1}{2} \cdot \pi \cdot r^2$ berechnen.

Wir berechnen zunächst die Mantelfläche der neuneckigen Pyramide. Dazu müssen wir zunächst die fehlenden Daten schätzen. Wir nehmen an, dass der Mensch ungefähr $1{,}70 \text{ m}$ groß ist. Wir schätzen daher mit dem Augenmaß, dass die Seitenhöhe des Tipis ungefähr $4{,}1 \text{ m}$ beträgt. Die Breite einer Grundkante schätzen wir auf ungefähr $1{,}3 \text{ m}$. Wir berechnen zunächst den Flächeninhalt einer einzelnen Seitenfläche (also eines Dreiecks) der neuneckigen Pyramide:

$A_{\text{Dreieck}}=\frac{1}{2} \cdot 1{,}3 \cdot 4{,}1=2{,}665 \text{ m}^{2} \approx 2{,}67 \text{ m}^{2}$

Als nächstes berechnen wir den Mantelflächeninhalt der Pyramide: $M=9 \cdot A_{\text{Dreieck}}=9 \cdot 2{,}67=24{,}03 \text{ m}^{2}$

Wir schätzen den Durchmesser des Halbkreises auf $1{,}3 \text{ m}$, da der Eingang ungefähr die Breite der Grundseite hat. Nun berechnen wir den Flächeninhalt des Halbkreises und ziehen diesen dann von der Mantelfläche ab:

$A_{\text{Halbkreis}}=\frac{1}{2} \cdot 0{,}65^2 \cdot \pi \approx 0{,}66 \text{ m}^{2} \Rightarrow A_{\text{gesucht}}=24{,}03-0{,}66=23{,}37 \text{ m}^{2}$

Für das Tipi werden ungefähr $23{,}37 \text{ m}^{2}$ Zeltplane benötigt.

weiter zum nächsten Kapitel