Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden konstruieren
Dieser Lernpfad befindet sich aktuell im Aufbau.
.
Pyramiden konstruieren
Wie ihr im letzten Kapitel schon gelernt habt, Begegnen uns Pyramiden sehr oft im Alltag.
Fallen euch konkrete Beispiele ein?
In diesem Kapitel lernst du Netze und Schrägbilder kennen.
Beides findet unter anderem in der Architektur und dem Bauingenieurwesen Anwendung.
0. Netze zuordnen
Das Netz eines Körpers dient dazu, dessen Flächen (perspektivisch unverzerrt) in der Ebene darzustellen. Dies erleichtert auch das Zusammenbauen dieses Körpers, z.B. aus Papier.
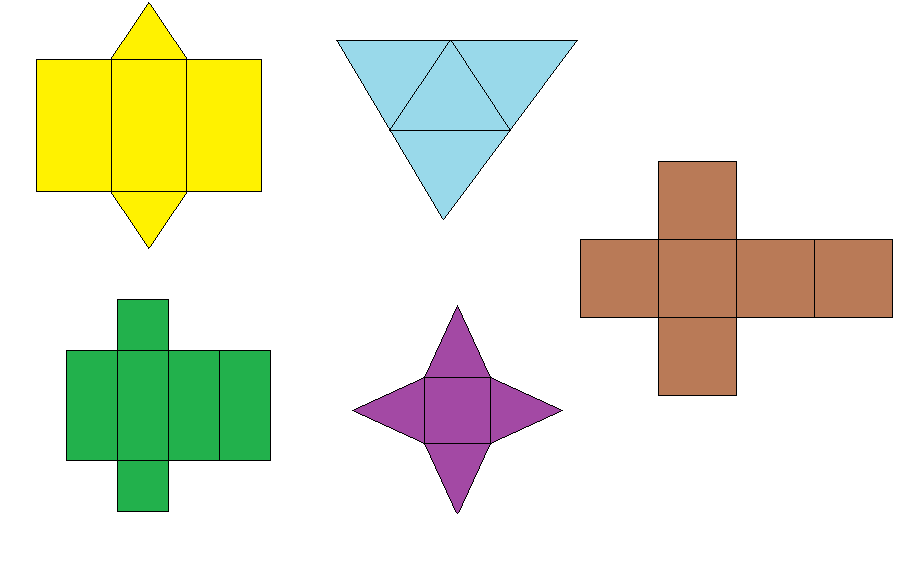
Aufgabe: Ordne den unten dargestellten Netzen den Körpern zu, die daraus gebaut werden können (Würfel, Pyramide mit dreieckiger Grundfläche, Quader, Dreiecksprisma, Pyramide mit quadratischer Grundfläche).
1. Netze entwerfen
1.1. Netz einer Pyramide mit quadratischer Grundfläche zeichnen
Hinweis: Deine Zeichnung soll nach dieser Anleitung im Wesentlichen so aussehen wie das lila dargestellte Netz aus der obigen Abbildung.
a) Zeichne zuerst ein Quadrat.
b) Zeichne als nächstes die Diagonalen in das Quadrat ein. Der Schnittpunkt der Diagonalen kennzeichnest du mit einem "S". (Verwirrende Bezeichnung "S"?)
c) Markiere nun auf den Seiten des Quadrats die Punkte, die auf der Mitte der Seiten liegen, indem du folgendes für alle vier Seiten tust: Lege das Geo-Dreieck so, dass eine Gerade entsteht, die durch S und senkrecht durch die jeweilige Seite verläuft. Somit erhältst du die Punkte, die mittig auf den Seiten liegen. Trage diese Punkte ab und nenne sie A, B, C bzw. D.
d) Zeichne nun, von den vier mittig auf den Seiten liegenden Punkten A bis D ausgehend, jeweils eine 4cm-lange Strecke ein; diese beginnt jeweils in den Punkten A (bzw. B, C, D), steht senkrecht auf der jeweiligen Seite des Quadrats und führt vom Quadrat weg. (Bezeichnung der Punkte?)
e) Verbinde nun die "Enden" der soeben erstellten Strecken mit den nächstliegenden Ecken des Quadrats, sodass vier Dreiecke entstehen, die das Quadrat umschließen.
1.2. Tetraeder erkunden
Nicht alle Pyramiden haben eine quadratische Grundfläche. Auch zum Beispiel ein Rechteck, Dreieck oder Sechseck können die Grundfläche einer Pyramide sein. Ein besonderer Fall einer Pyramide mit dreieckiger Grundfläche ist der Tetraeder.
a) Zeichne nun selber das Netz eines Tetraeders.
Wenn du Hilfe benötigst, kannst du die Anleitung verwenden.
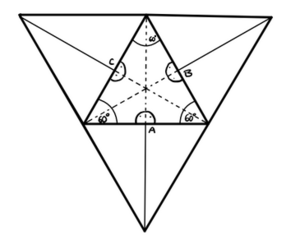
1. Beginne mit der Grundfläche. Achte dabei darauf, dass diese ein gleichseitiges Dreieck ist und somit auch gleichwinklig ist.
2. Zeichne drei Hilfslinien ein. Von der Spitze des Dreiecks bis zur Mitte der gegenüberliegenden Seite. Die Hilfslinien stehen dabei im 90° Winkel zur jeweiligen Seite. Bezeichne die Schnittpunkte mit A, B, und C.
3. Miss nun die Länge der Hilfslinien.
4. Zeichne nun von den Punkten A, B, C die Seitenhöhen ein. Diese sind genauso lang wie die Hilfslinien.
5. Verbinde nun die "Enden" der erstellten Strecken mit den nächstliegenden Ecken des Dreiecks, sodass drei Dreiecke entstehen, die die Grundfläche umschließen.Um deine Zeichnung zu kontrollieren, kannst du sie mit der Musterlösung vergleichen.
Implementierung von Applet wie Geogebra: Pyramide zeichnen (3D), mit Regler so verschieben, dass es Tetraeder wird: Was fällt euch auf. Idee: Ecken der Grundflächen mit Regler verändern.
2. Körper herstellen
Eben hast du das Netz einer Pyramide mit quadratischer Grundfläche und vielleicht auch das eines Tetraeders gezeichnet. Nun soll aus diesem Netz ein dreidimensionaler Körper durch Auffalten des Netzes hergestellt werden.
Nachfolgend ist die Herstellung einer Pyramide dargestellt. Ziehe den Schieberegler nach rechts, um die Mantelflächen der Pyramide aufzurichten. Um die Form der Pyramide zu verändern, kannst du deren Eckpunkte verschieben; dadurch wird auch das Netz verändert.

2.1. Pyramide mit quadratischer Grundfläche
Stelle aus dem eben angefertigen Netz aus 1.1. eine Pyramide mit quadratischer Grundfläche her.
a) Nimm das Netz, was du in Aufgabe 1.1 erstellt hast und lege es vor dich hin. Falls du diese Aufgabe übersprungen hast, gehe zurück und zeichne ein Netz.
b) Schneide das Netz aus.
c) Falte die Seitenflächen entlang der Kanten des Quadrats, jeweils an den Punkten A,B,C und D.
d) Jetzt kannst du die Seitenflächen an der oberen Spitze zusammenfügen. Das ist dann die Spitze deiner Pyramide.
e) Du kannst deine Pyramide an den Seiten mit etwas Tesafilm fixieren, wenn du möchtest.
3. Schrägbilder skizzieren
3.1. Pyramide mit quadratischer Grundfläche
Ziel: die räumliche Zeichnung (also das Schrägbild) einer Pyramide mit quadratischer Grundfläche anfertigen
a) Überlege wie du vorgehst, wenn du das Schrägbild einer Pyramide mit quadratischer Grundfläche zeichnen kannst.
Zeichne ein Schrägbild mit Kantenlänge a= 5cm und der Höhe h= 6cm.

3.2. Pyramide mit n-eckiger Grundfläche
Ziel: das Schrägbild einer Pyramide mit n-eckiger anfertigen
a) Überlege dir, welche Grundfläche deine Pyramide haben soll (Bsp.: dreieckige, quadratische, sechseckige Grundfläche).
b)
4 Sicherung
Lückentext oder Pyramide basteln lassen