Digitale Werkzeuge in der Schule/Rund ums Dreieck/Winkel an Geraden

Info

In diesem Lernpfadkapitel lernst du zwei Sätze kennen, mit denen Winkel an Gerade bestimmt werden können.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

 

Winkel messen

Aufgabe 1: Winkel in der Parkettierung

zurück zum Arbeitsblatt

Parkettierung mit eingezeichneten Winkeln.

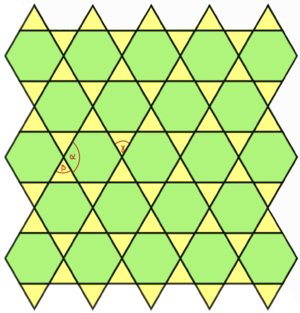
Betrachte die Abbildung. Tim möchte die Größen der Winkel $\alpha$, $\beta$ und $\gamma$ untersuchen. Bestimme die Winkel, um Tim zu helfen. Die Abbildung findest du auch auf dem Arbeitsblatt.

$\alpha$= 120()°
$\beta$= 60()°
$\gamma$= 60()°

Erinnere dich daran, dass Winkel mit dem griechischem Alphabet beschrieben werden. Typische Bezeichnungen für Winkel sind

• $\alpha$ (Alpha, griechisches a)
• $\beta$ (Beta, griechisches b)
• $\gamma$ (Gamma, griechisches g)

Wenn du weitere Buchstaben aus dem griechischem Alphabet benötigst, schaue gerne unter diesem Wikipedia-Link nach: https://de.wikipedia.org/wiki/Griechisches_Alphabet

Erkundung

Nachdem du für Tim die Winkel gemessen hat, fällt ihm auf, dass der Winkel $\gamma$ gleich groß ist, wie der Winkel unter $\beta$. Tim behauptet: "Die gegenüberliegenden Winkel an zwei Geraden, die sich schneiden, sind immer gleich groß".

Hat Tim recht?

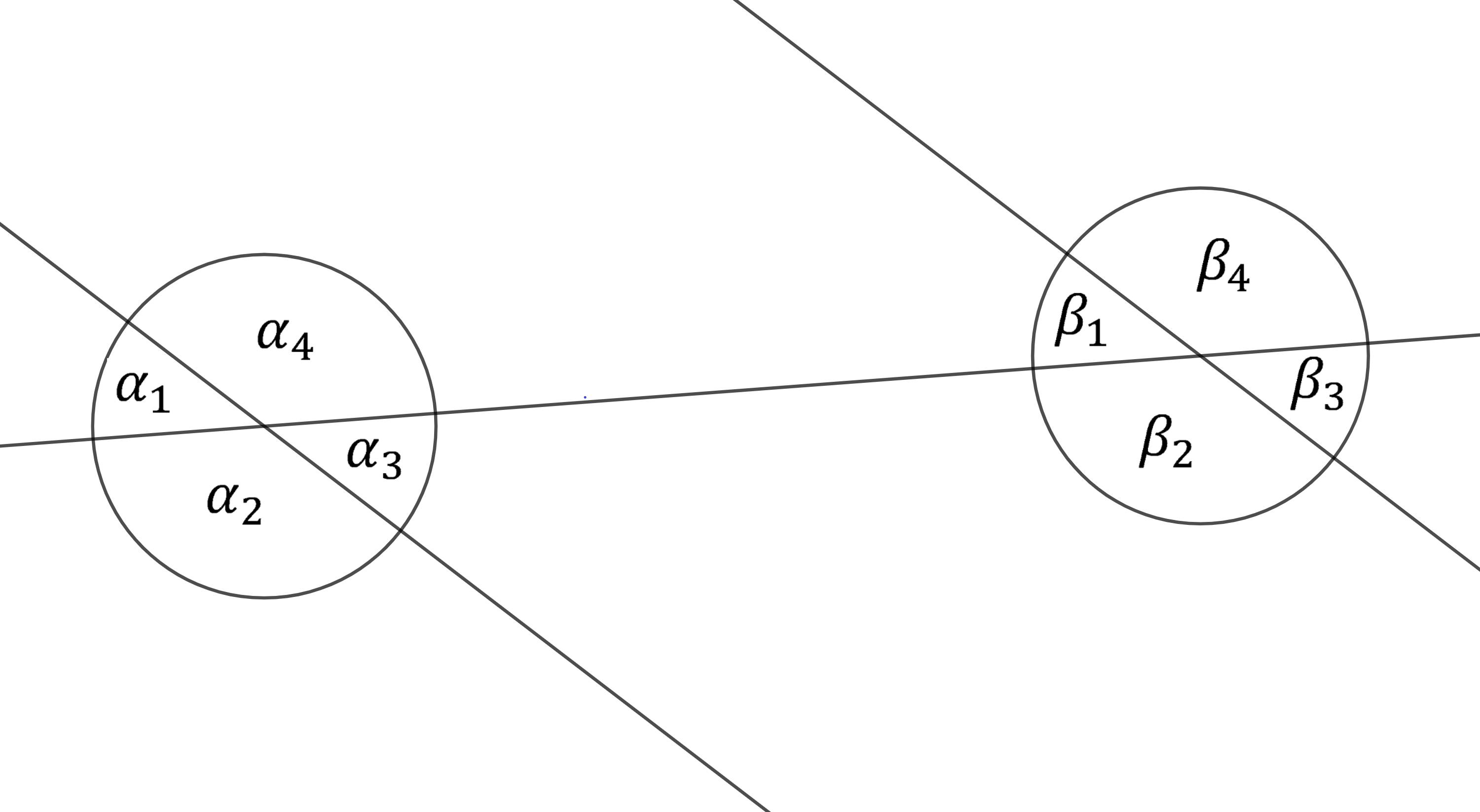
Überprüfe Tims Behauptung, indem du das unten stehende GeoGebra-Applet untersuchst. Fülle danach den unten stehenden Lückentext aus.

(Applet von I. Schwalbe)

Wenn die Lage der beiden Geraden zueinander verändert wird, so verändern sich auch die Winkel am Schnittpunkt. Zwei sich gegenüberliegende Winkel bleiben auch beim verändern der Lage der Geraden zueinander gleich groß. Zwei nebeneinander liegende Winkel (z.B.$\alpha$ und $\beta$) ergänzen sich zusammen immer zu 180°, deshalb nennt man sie auch Nebenwinkel. Wenn nun alle Winkel addiert werden, so ergibt $\alpha$+$\beta$+$\gamma$+$\delta$ =360°.

Tim hat also recht. Die Winkel, die sich beim schneiden von zwei Geraden gegenüberliegen, sind tatsächlich gleichgroß. Weil sie gleichgroß sind und sich wie ein Scheitel gegenüber liegen, haben sie einen besonderen Namen. Diesen wollen wir in einem Merksatz festhalten:

Merksatz: Scheitelwinkel

zurück zum Arbeitsblatt

Scheitelwinkel

Übertrage diesen Merksatz auf das Arbeitsblatt und zeichne zwei Scheitelwinkel in die Abbildung ein.

Schneiden sich zwei Geraden in einem Schnittpunkt, so nennen wir die Winkel die sich gegenüberliegen, Scheitelwinkel. Diese Scheitelwinkel sind immer gleich groß.

Aufgabe 3: Wie kann das sein?

zurück zum Arbeitsblatt

Tom, Tims Freund, versteht nicht, warum das so ist. Hilf Tim, eine Begründung für Tom zu finden. Schaue dir hierfür das folgende Video an und halte deine Begründung auf dem Arbeitsblatt fest.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Winkel an mehreren Geraden

Tim und Tom haben nun beide verstanden, dass Scheitelwinkel gleich groß sind. Auf dem Bild am Anfang sind jedoch drei Geraden, von denen zwei parallel zueinander liegen. Sie fragen sich nun, ob es bei mehreren Geraden ebenfalls Winkel gibt, die gleich groß sind.

Aufgabe 4: Stufenwinkel erkunden

Also werden nun zwei parallele Geraden, die von einer dritten Gerade geschnitten werden, betrachtet. Schaue dir dieses weitere GeoGebra-Applet an und untersuche dieses, indem du die Position der Geraden zueinander veränderst. Vergleiche die Winkel miteinander und ergänze danach den unten stehenden Merksatz.

(Applet von B. Lachner)

Merksatz: Stufenwinkel

zurück zum Arbeitsblatt

Stufenwinkel

Fülle den unten stehenden Lückentext aus und schreibe ihn danach auf das Arbeitsblatt ab. Zeichne zwei Stufenwinkel in die Abbildung ein.

Wenn zwei parallele() Geraden von einer dritten Gerade geschnitten werden, entstehen zwei() Schnittpunkte. Betrachtet man die Winkel $\alpha$ und $\beta$, so nennen wir diese Art von Winkeln Stufenwinkel(), welche gleich groß() sind.

Schaue dir das folgende Video nochmal an, um den Zusammenhang zwischen den Winkel noch besser zu verstehen.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Folgende Begriffe könnten dir vielleicht helfen

• zwei
• Stufenwinkel
• parallele
• gleich groß

Aufgabe 5: Zuordnung

Nachdem Tim und Tom jetzt wissen, was Neben-, Scheitel- und Stufenwinkel sind, hat Tom sich für Tim Geraden und Winkel ausgedacht und aufgezeichnet. Um das ganze jedoch noch schwieriger und unübersichtlicher zu gestalten, hat er mehr Linien und Winkel eingezeichnet, als nötig wären. Tim braucht wieder deine Hilfe. Ordne den Bilder die passende Unterschrift zu.

Wenn du dir nicht mehr sicher bist, scrolle auf der Seite weiter nach oben und schaue dir die jeweiligen Winkeltypen noch einmal an. Welche der Geraden sind wichtig zu beachten?

Welche der Geraden sind parallel?

Übungsaufgaben

Nachdem Tim und Tom sich jetzt mit Scheitel- und Stufenwinkeln auskennen, haben sie sich ein paar Übungsaufgaben für dich ausgedacht. Kannst du sie lösen?

Aufgabe 6: Scheitel- und Stufenwinkel erkennen

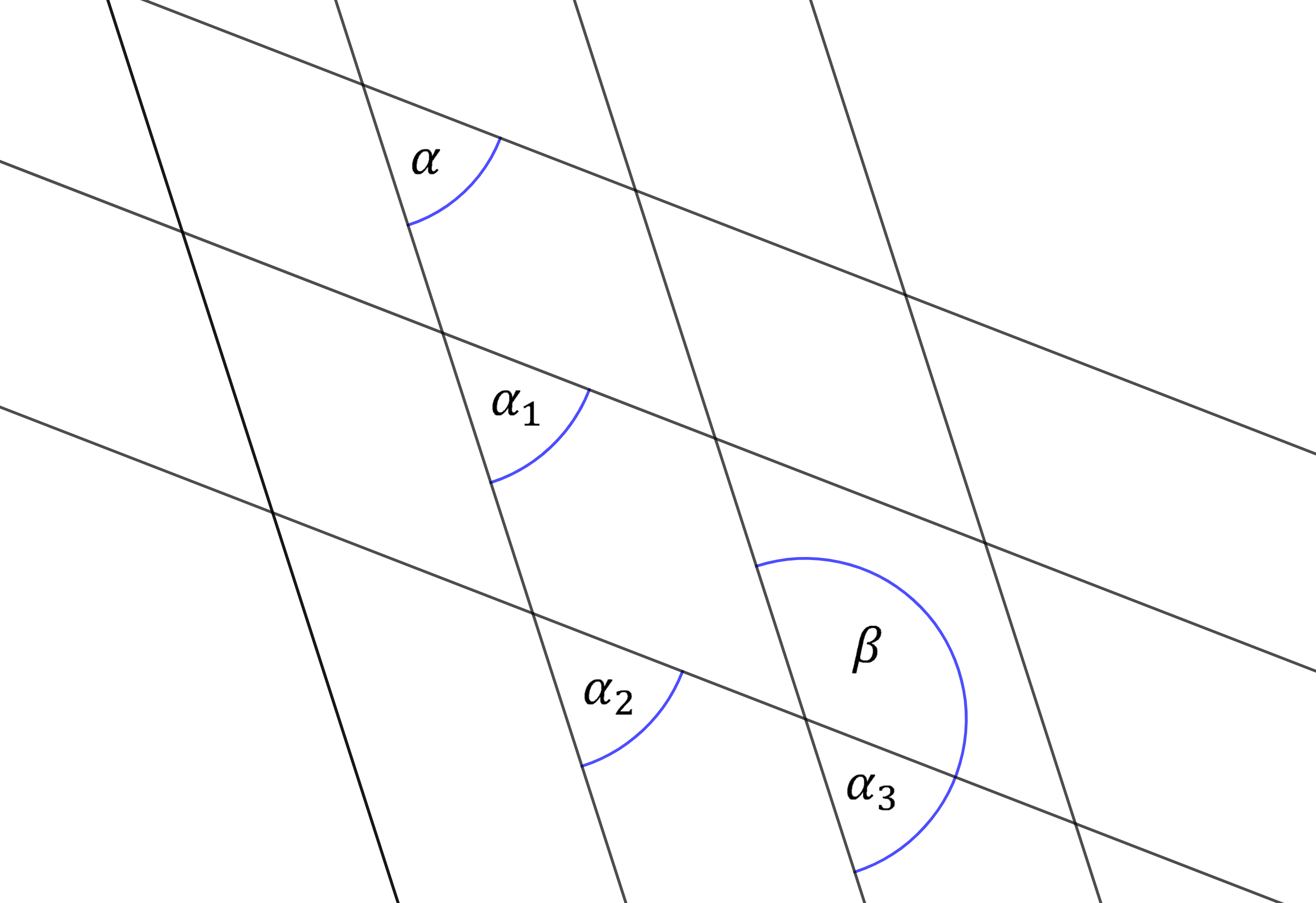
Die Abbildung zeigt drei Geraden, von denen zwei parallel sind. Überlege dir welche der Aussagen korrekt sind. Schreibe "richtig" oder "falsch" hinter die Aussagen.

1. $\alpha_{1}$ und $\alpha_{3}$ sind Scheitelwinkel. richtig()
2. $\alpha_{1}$ und $\alpha_{2}$ sind Stufenwinkel. falsch()
3. Zu jedem der Winkel gibt es in der Abbildung einen Stufenwinkel und einen Scheitelwinkel. richtig()
4. Zu einigen der Winkel gibt es mehrere Stufenwinkel. falsch()
5. $\alpha_{1}$ und $\beta_{1}$ sind Stufenwinkel. richtig()
6. $\alpha_{2}$ ist ein Stufenwinkel zu $\beta_{2}$ und $\beta_{2}$ ist ein Scheitelwinkel zu $\beta_{4}$. Also sind $\alpha_{2}$ und $\beta_{4}$ gleich groß. richtig()

Aufgabe 7: Bayrische Flagge

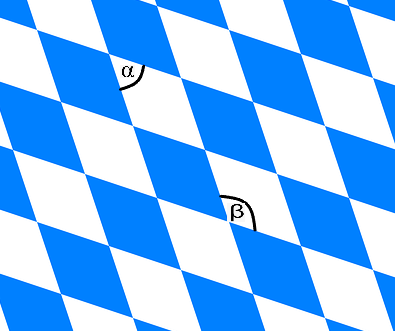
Das Bild zeigt einen Ausschnitt der bayrischen Flagge mit den eingezeichneten Winkeln $\alpha$ und $\beta$. Der Winkel $\alpha$ ist 51° groß. Wie groß ist der Winkel $\beta$? Begründe die Antwort mit Hilfe deines Wissens über Stufenwinkel, indem du den Lückentext ausfüllst.

In die bayrische Flagge kann man zwei Geraden einzeichnen, sodass $\alpha$ der Schnittwinkel der beiden Geraden ist. Alle anderen Geraden, die das Rautenmuster bilden, sind jeweils zu einer der beiden Geraden parallel.

Wenn man nun vom Winkel $\alpha$ aus entlang einer der beiden Geraden geht, so kann man bei jeder Geradenkreuzung einen Stufenwinkel zu $\alpha$ einzeichnen. Man kann zum Beispiel entlang der steileren Gerade nach unten wandern und dann bei dem zweiten Schnittpunkt einen Stufenwinkel von $\alpha$ einzeichnen, den wir $\alpha_{2}$ nennen. Dieser befindet sich in der oberen Ecke einer weißen Raute.

Den Winkel unterhalb von $\beta$, also in der oberen Ecke der blauen Raute nennen wir $\alpha_{3}$. $\alpha_{3}$ ist dann wiederum ein Stufenwinkel zu $\alpha_{2}$. Da Stufenwinkel gleich groß sind, sind also die Winkel $\alpha$,$\alpha_{2}$ und $\alpha_{3}$ alle $60$° groß. Die Winkel $\alpha_{3}$ und $\beta$ sind Nebenwinkel und ergänzen sich zu 180°.

Also ist $\beta$ dann 129()° groß.

In dieser Skizze sieht man die Geraden, durch die das Rautenmuster der bayrischen Flagge entsteht. Dabei sind Winkel eingezeichnet, mit denen man $\beta$ bestimmen kann.

Aufgabe 8: Leiter an der Hauswand

zurück zum Arbeitsblatt

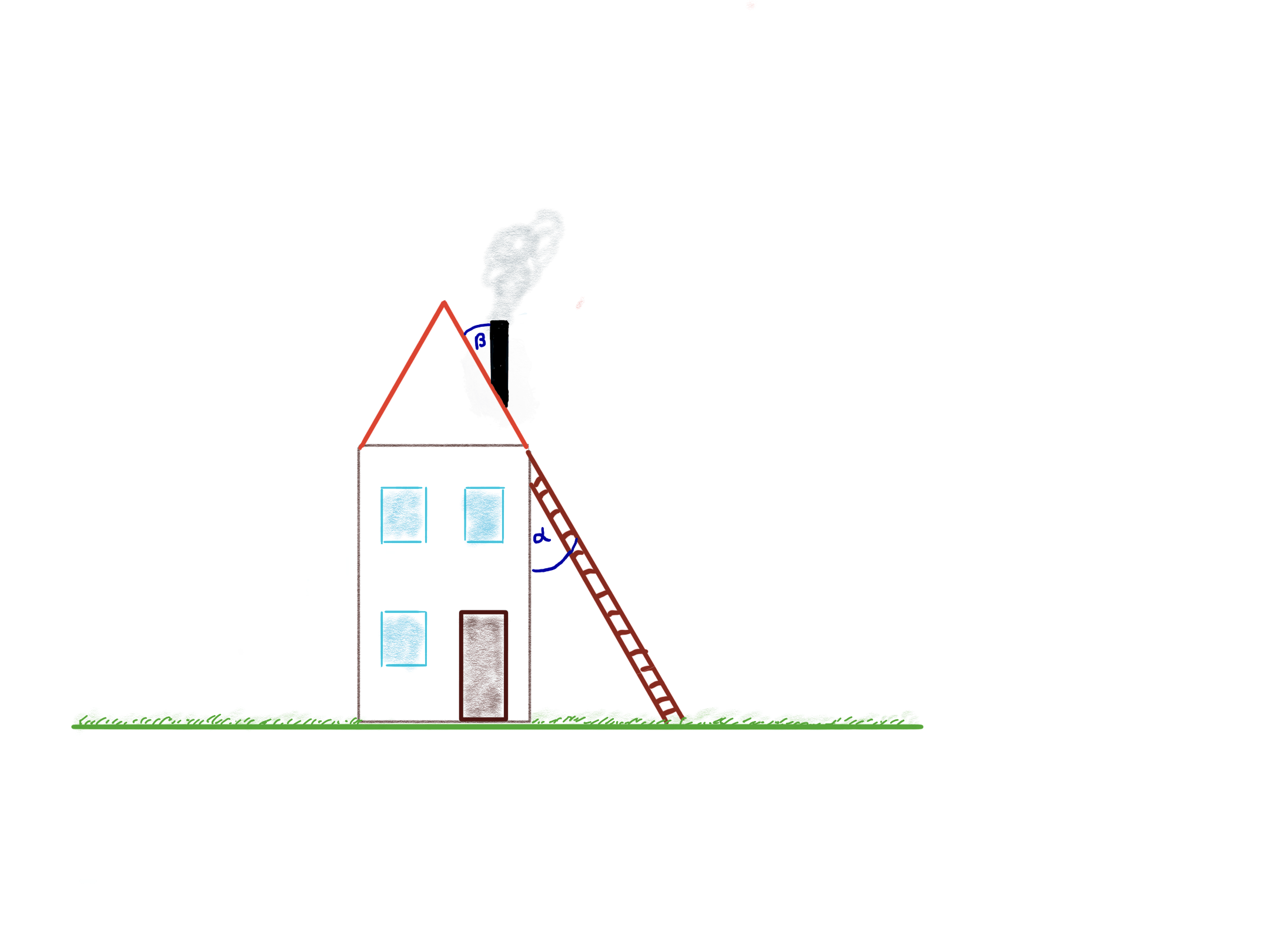
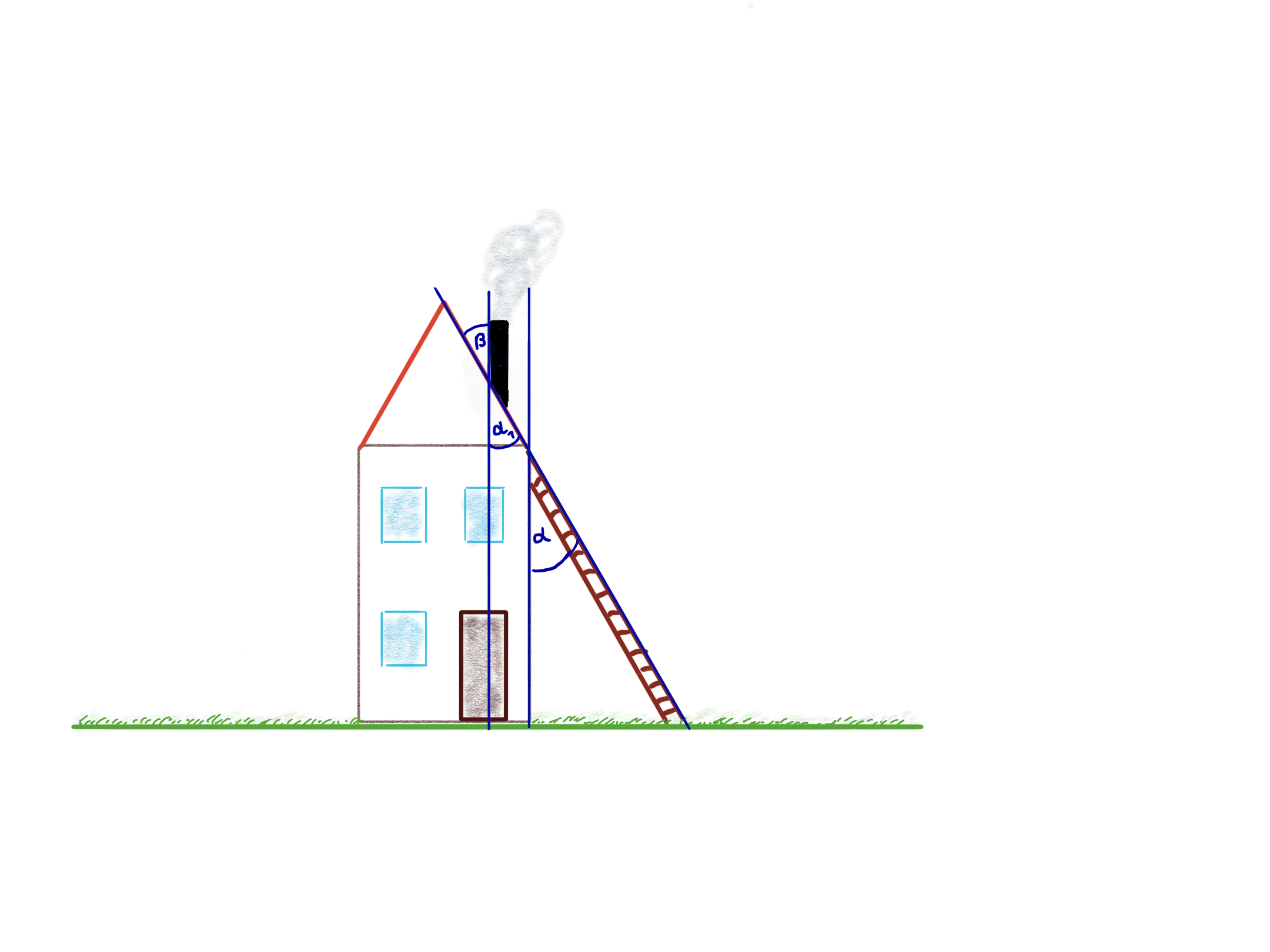
Eine Leiter steht an einer Hauswand, so dass sie mit dem Dach eine gerade Linie bildet. Es ist $\alpha$=60° bekannt. Bestimme den Winkel $\beta$ zwischen dem Schornstein und dem Dach. Du kannst, wenn du möchtest, als Hilfe Geraden und Winkel in die Abbildung auf dem Arbeitsblatt einzeichnen.

Es hilft als erstes zu überlegen, wo es Geraden und Winkel geben könnte und diese einzuzeichnen. Gibt es irgendwo parallele Geraden? In welchem Winkel treffen die Hauswand und die Verlängerung des Schornsteins auf den Boden

Man kann entlang der Hauswand und entlang des Schornsteins zwei parallele Geraden und eine weitere Gerade entlang des Daches des Hauses einzeichnen. Der Winkel $\alpha_{1}$ in der Zeichnung ist ein Stufenwinkel zu $\alpha$ und ein Scheitelwinkel zu $\beta$.

Der Winkel $\beta$ ist 60()° groß.

zurück zur Kapitelauswahl