Diese Seite befindet sich im Aufbau.
Info
In diesem Lernpfadkapitel lernst Eigenschaft für die Winkel in Dreiecken gibt. Diese werden wir in einer Regel festhalten und du übst, wie man sie richtig anwendet.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Muster untersuchen
Aufgabe 1: Winkel im Kreis
Parkettierung mit Dreiecken
Betrachte ein blaues Dreieck in der Abbildung auf der rechten Seite. Tim behauptet, er kann die Größe aller grünen Winkel ganz einfach bestimmen ohne Nachmessen zu müssen. Gibst du ihm recht? Bestimme im Anschluss die Größe eines grünen Winkels.
Wieviele Spitzen treffen aufeinander, damit ein Kreis gebildet wird?
Ein Kreis besitzt 360°
Erforschung
Die Winkel in den Dreiecken oben sind also alle gleichgroß. Allerdings waren die Dreiecke oben auch alle gleichseitig. Gibt es trotzdem eine Regel, die sich auf alle Dreiecke anwenden lässt?
In den folgenden Aufgaben wirst du genau das untersuchen und versuchen selbst die Regel herauszufinden, mit der du einen (oder mehrere) Innenwinkel in jedem Dreieck bestimmen kannst ohne jedes Mal nachmessen zu müssen.
Gleichseitige Dreiecke
Aufgabe 2: Winkel im gleichseitigen Dreieck
Notiere dir auf dem Arbeitsblatt, was mit den Innenwinkeln des Dreiecks passiert, egal wie lang die Seitenlänge des Dreiecks ist.
zurück zum Arbeitsblatt
Verschiebe das gleichseitige Dreieck beliebig und vergrößere oder verkleinere es an den Punkten A und B.
Die Innenwinkel bleiben gleich. Egal wie du die Punkte A und B verschiebst, solange die Winkel gleich bleiben handelt sich weiterhin um ein gleichseitiges Dreieck.
Allgemeine Dreiecke
Aufgabe 3: Winkel im allgemeinen Dreieck
Erstelle ein beliebiges Dreiecke mit der App. Notiere dir auf dem Arbeitsblatt, was für eine Eigenschaft die Winkel in einem beliebigen Dreieck haben. zurück zum Arbeitsblatt
Wiederhole dies im Anschluss mit einem anderen Dreieck.
Du kannst das Dreieck an den Ecken in eine beliebige Form ziehen. Klicke danach auf Start und folge den Anweisungen des Applets.
Hinweis:
Für die nächste Aufgabe solltest du Kapitel 2: Winkel an Geraden schon bearbeitet haben und wissen, was Scheitel- und Stufenwinkel sind. Wenn das nicht der Fall ist, kannst du diese Aufgabe einfach überspringen.
Wenn du aber schon Kapitel 2 bearbeitet hast, zeigt dir die folgende Forschungsaufgabe noch eine weitere Begründung für die Innenwinkelsumme in Dreiecken ohne die Winkel umständlich verschieben zu müssen, sondern nur mithilfe einer Hilfslinie. Dieser Lösungsweg kann später bei einigen Anwendungsaufgaben sehr nützlich sein!
Aufgabe 4: Stufen- und Wechselwinkel im Dreieck
Ziehe das Dreiecke in beliebige Formen. Notiere dir auf dem Arbeitsblatt, warum die grünen bzw. blauen Winkel immer gleich groß sind und welche Eigenschaft die Winkel zusammen haben. zurück zum Arbeitsblatt
Innenwinkelsumme im Dreieck
Notiere dir den Merksatz auf deinem Arbeitsblatt.
Merksatz: Der Innenwinkelsummensatz für Dreiecke
Die Innenwinkelsumme eines Dreiecks beträgt immer 180°.
Für die drei Winkel alpha, beta und gamma gilt also:
α+β+γ ergeben 180°
Auch hier ergeben die drei Winkel insgessamt 180°
Aufgaben
Bearbeite nun die untenstehenden Aufgaben. Beginne mit Aufgabe 5. Falls dir die Rechnungen leicht fallen, kannst du auch direkt zu Aufgabe 6 weitergehen. Wenn du Platz brauchst, um deine Rechnungen zu notieren, kannst du hierfür den Platz auf dem Arbeitsblatt nutzen. zurück zum Arbeitsblatt
Aufgabe 5: Ergänze die Tabelle
Wende den Innenwinkelsummensatz an und berechne den fehlenden Winkel.
Aufgabe 6: Innenwinkel-Quiz
Gib jeweils den/die fehlende(n) Winkel an. Trenne mehrere Zahlen durch ein Komma.
Hinweis: Es reicht die Zahl anzugeben, du musst kein Gradzeichen ° eintippen.
Beispiel:
α = 30°, β = 70°
Lösung: 80
Aufgabe 7: Innenwinkel-Quiz (Experte)
Gib die Innenwinkel der Dreiecke an. Nutze dazu alles, was du zu Winkeln an einer Geraden, dem Innenwinkelsummensatz, Stufenwinkeln und Scheitelwinkeln weißt.
Hinweis: Es reicht die Zahlen ohne Gradzeichen ° anzugeben und durch ein Leerzeichen zu trennen.
Beispiele für die Lösungseingabe:
50 60 70
45,5 54,3 80,2
Anwendungsaufgabe
Rutschenproblem
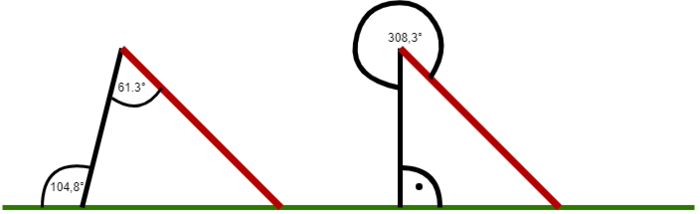
Um herauszufinden, wie steil eine Rutsche ist, kann man den Winkel zwischen Rutschfläche und Boden betrachten.
Berechne die in Tipp 1 erwähnten Winkel für beide Rutschen und vergleiche beide.
Tim will während der großen Pause rutschen. Tim ist sich jedoch nicht sicher, welche Rutsche steiler sein könnte. Vor der Rutsche befindet sich der Plan der beiden Rutschen, wo einige Winkel eingezeichnet sind. Jedoch fehlen einige. Wie kann Tim sein Wissen aus dem Matheunterricht nutzen, um herauszufinden, welche der beiden Rutschen steiler ist.
.svg){kind=icon}
zurück zum Arbeitsblatt
