Digitale Werkzeuge in der Schule/Rund ums Dreieck/Winkel an Geraden

Diese Seite befindet sich zur Zeit im Aufbau

Einstieg

Aufgabe 1: Winkel an Geraden

Parkettierung mit Dreiecken.

Betrachte die Abbildung. Tim behauptet: "Es reicht aus, einen Winkel zu messen. Dann kann ich alle anderen Winkel bestimmen."

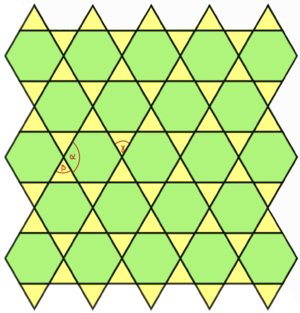
Ausschnitt der Parkettierung mit eingezeichneten Winkeln.

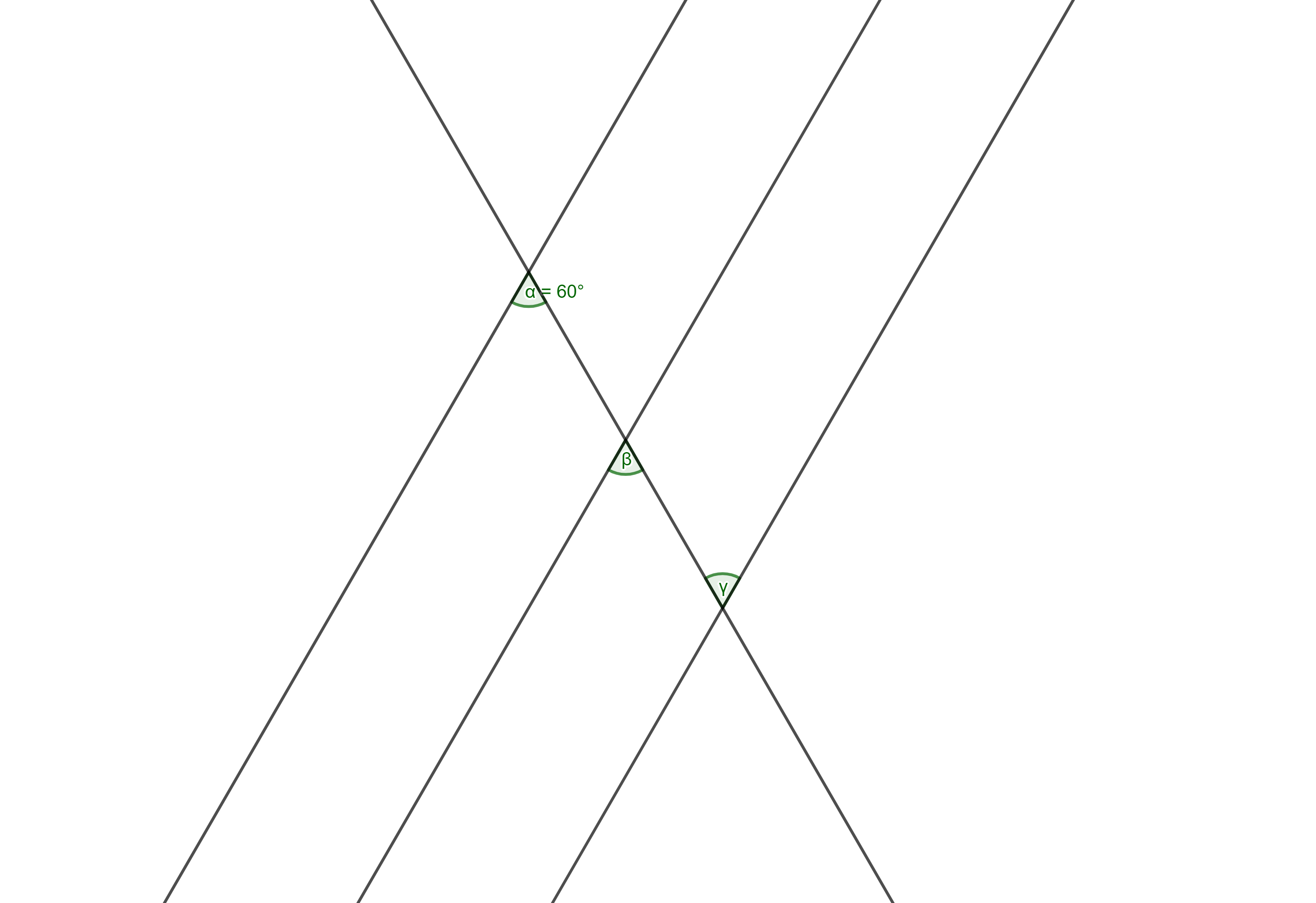
Schaue dir die Winkel in der zweiten Abbildung an. Tim konnte $\alpha=120^{\circ}$ bestimmen. Überprüfe Tims Behauptung, indem du die Winkel $\beta$ und $\gamma$ bestimmst.

$\beta$=

$\gamma$=

neu starten

Tipp

Erinnere dich daran, dass Winkel mit dem griechischem Alphabet beschrieben werden. Typische Bezeichnungen für Winkel sind

• $\alpha$ (Alpha, griechisches a)
• $\beta$ (Beta, griechisches b)
• $\gamma$ (Gamma, griechisches g)

Wenn du weitere Buchstaben aus dem griechischem Alphabet benötigst, schaue gerne unter diesem Wikipedia-Link nach: https://de.wikipedia.org/wiki/Griechisches_Alphabet

Erarbeitung

Scheitelwinkel

Aufgabe 2: Grundlagen zu Scheitelwinkeln

1. Untersuche das folgende GeoGebra-Applet, indem du dir die Winkel anzeigen lässt und die Position der Geraden veränderst. Verschiebe hierfür die Punkte A und B.

2. Beschreibe danach deine Beobachtungen, indem du den unten stehenden Lückentext ausfüllst.

(Applet von I. Schwalbe)

Wenn ich die Lage der Geraden zueinander verändere, so verändern sich auch am Schnittpunkt. Außerdem bleiben die Winkel $\alpha$ und $\beta$ , genau so wie die Winkel $\gamma$ und $\delta$. Zwei nebeneinander liegende Winkel addieren sich immer zu . Deshalb ergibt $\alpha +\beta +\gamma +\delta=$ .

die Winkel$360^\circ$$180^\circ$gleich groß

neu starten

Aufgabe 3: Erklärung Scheitelwinkel

Warum sind Scheitelwinkel gleich groß? Begründe deine Beobachtungen aus Aufgabe 2 mit geometrischen Argumenten.

Tipp

Welche der folgenden Begriffe aus der Geometrie könnten dir bei deiner Begründung helfen?

Klicke die Begriffe an, die dir helfen könnten.

	Drehung
	Spiegelung
	Verschiebung

Lösung

Beweisidee/Lösung

Aufgabe 4: Beweis

Kannst du mit mathematischen Formel erklären, warum Scheitelwinkel gleich groß sind?

Tipp

Was weißt du über gestreckte Winkel? Betrachte alle Winkel um den Schnittpunkt der Geraden und dein Wissen über gestreckte Winkel.

Lösung

Da sich zwei Nebenwinkel zu $180^\circ$ ergänzen gilt $\alpha+\beta=180^\circ$. Da $\beta$ und $\gamma$ auch einen gestreckten Winkel bilden, gilt ebenfalls $\beta+\gamma=180^\circ$. Werden nun diese beiden Gleichungen voneinander subtrahiert, so gilt $\alpha+\beta-(\beta+\gamma)=180^\circ-180^\circ$. Durch Umstellen ergibt sich also $\alpha =\gamma$.

Merksatz: Scheitelwinkel

Scheitelwinkel

Übertrage diesen Merksatz mit einer Skizze in dein Regelheft.

Schneiden sich zwei Geraden, so nennen wir die Winkel die sich gegenüberliegen, Scheitelwinkel. Diese Scheitelwinkel sind immer gleich groß.

Stufenwinkel

Aufgabe 3: Stufenwinkel erkunden

Betrachten wir nun zwei parallele Geraden, die von einer dritten Gerade geschnitten werden. Schaue dir hierfür ein weiteres GeoGebra-Applet an und untersuche dieses, indem du die Position der Geraden zueinander veränderst. Was fällt dir auf?

(Applet von B. Lachner)

Merksatz: Stufenwinkel

Stufenwinkel

Vervollständige auf Grund deiner Beobachtungen den Merksatz und schreibe ihn danach mit einer Skizze in dein Regelheft.

Stufenwinkel sind .

neu starten

Anwendung

-Bild einfügen (Fliesenmuster Rauten, Bayern Flagge,...)

In dieser Aufgabe kannst du nun dein Wissen über die Winkelarten anwenden. Wie groß ist der Winkel $\beta$ im obigen Bild? Begründe deine Antwort, mit Hilfe deines Wissens über Stufen- und Wechselwinkel. Du kannst selber entscheiden, ob du zum Schrittweisen Lösen die Aufgaben 4a) und 4b) bearbeitest oder direkt die Frage beantwortest und begründest.

Aufgabe 4a): Anwendungsaufgabe

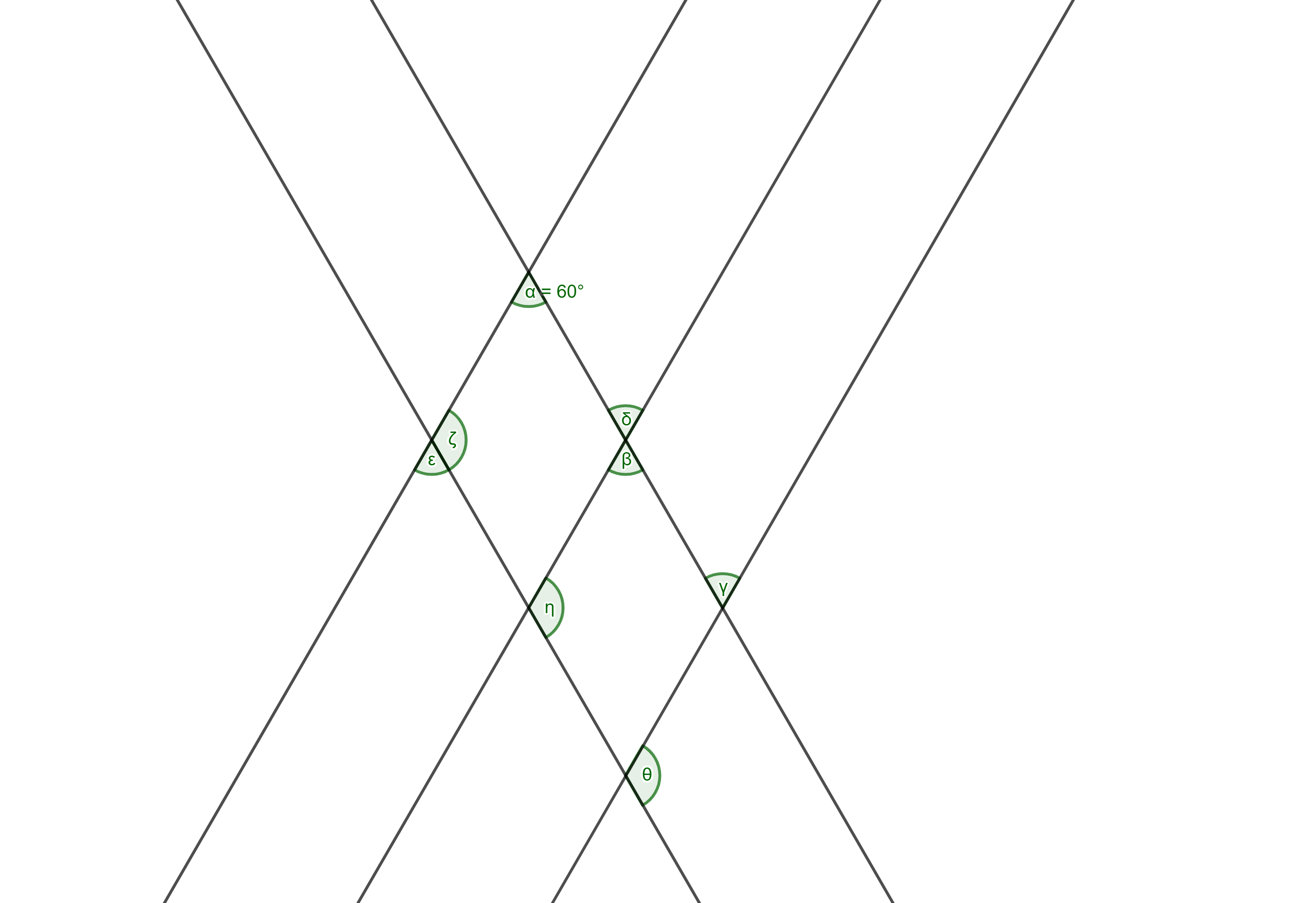
Bestimme die fehlenden Winkel!

Aufgabe 4b): Anwendungsaufgabe

Bestimme die fehlenden Winkel!

Transferaufgabe

Leiter an der Hauswand

Aufgabe 5: Anwendungsaufgabe

Eine Leiter steht an einer Hauswand, so dass sie mit dem Dach eine gerade Linie bildet. Es soll nun der Winkel $\gamma$ zwischen dem Schornstein und dem Dach bestimmt werden.

Tipp 1 anzeigen

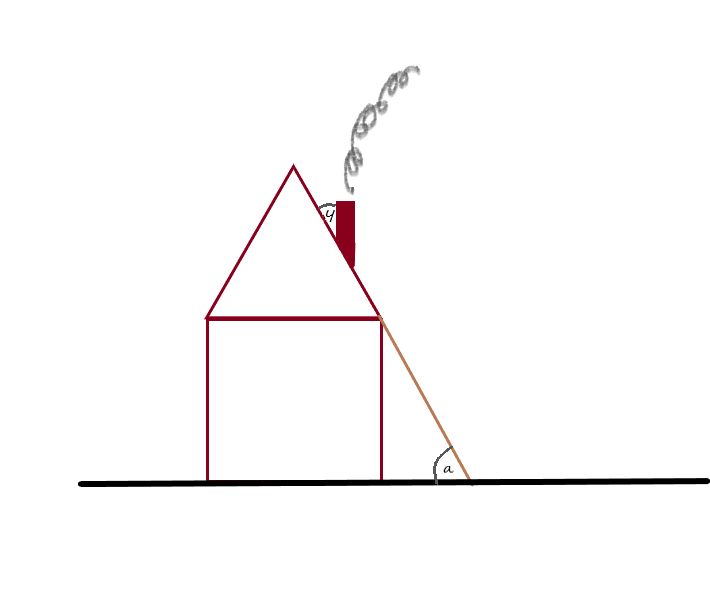
Es kann helfen sich als erstes zu überlegen, wo es denn Geraden und Winkel geben könnte und diese einzuzeichnen. Gibt es irgendwo parallele Geraden? Dazu kann es hilfreich sein sich zu überlegen in welchem Winkel die Hauswand und der Schornstein (beziehungsweise eine Verlängerung des Schornsteins) auf den Boden treffen

Tipp 2 anzeigen

Die Leiter, der Boden und die rechte Hauswand bilden ein Dreieck. Zeichne es ein und überleg dir wie groß die Innenwinkel sind.

Tipp 3 anzeigen

- Bild mit eingezeichneten Winkeln und Geraden einfügen

Hauswand, Leiter und Boden bilden ein rechtwinkliges Dreieck. Die Summe der Innenwinkel beträgt 180°, damit lässt sich der Winkel $\beta$ bestimmen. Der Winekl $\beta$ ist ein Wechselwinkel zu dem Winkel $\gamma$.