Digitale Werkzeuge in der Schule/Rund ums Dreieck/Winkel an Geraden

Diese Seite befindet sich zur Zeit im Aufbau

Einstieg

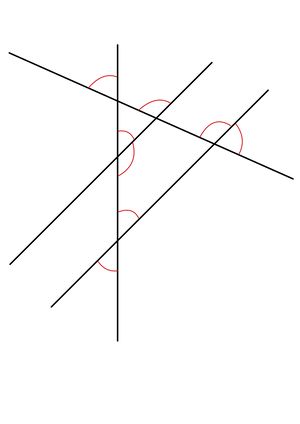
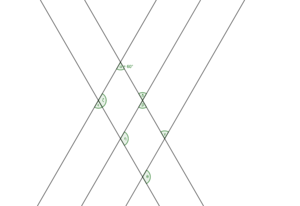
• Abbildung von vier Geraden, zwei Parallelen und zwei sich schneidenden Geraden.

Aufgabe 1: Winkel an Geraden

Betrachte die Abbildung und messe die gekennzeichneten Winkel. Was fällt dir auf? Beschreibe Auffälligkeiten.

• bestimmte Winkel sind markiert
• offene Aufgabe: Was fällt auf?
• Anschließendes GeoGebra-Padlet mit der gleichen Situation; alternativ: Abbildung auf Arbeitsblatt, sodass mit dem Geodreieck gemessen werden kann.
• Aufgabe: Winkel messen => Oh wow, die sind ja gleich!

Wiederholung

Nebenwinkel

Aufgabe 1: Grundlagen zu Nebenwinkeln

Bearbeite zur Wiederholung diese Aufgaben. Wenn du nicht weiter weißt, kannst du einen Tipp anfordern.

Nebenwinkel

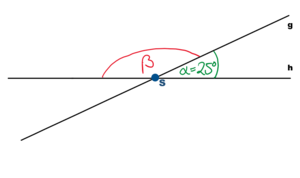
a)In dem Bild rechts schneiden sich zwei Gerade g und h in einem Schnittpunkt S und schließen einen Winkel $\alpha=25^\circ$ ein. Wie groß ist der Winkel $\beta$?

Vielleicht hilft es dir weiter, dass ein Kreis $360^\circ$ hat. Wie viel Grad hat dann ein halber Kreis?

Tipp

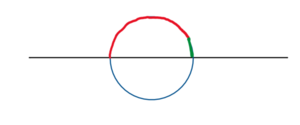
Schaue dir das Bild rechts an. Der rot/grüne Halbkreis oberhalb der Geraden besitzt $180^\circ$. Erkennst du Gemeinsamkeiten zu dem Bild zur Aufgabe?

Der Winkel $\beta$ beträgt 155() Grad.

b)Kannst du eine allgemeine Formel aufschreiben, wie sich zwei Nebenwinkel ($\alpha$ und $\beta$) zueinander verhalten? Überlege dir erst selbst eine Gleichung und wähle danach die richtige aus.

Welche der folgenden Gleichungen ist richtig?

	$\alpha + \beta = 360^\circ$
	$\beta = \alpha - 180^\circ$
	$\alpha - \beta = 360^\circ$
	$\alpha = 180^\circ - \beta$
	$\alpha - \beta = 180^\circ$

Setze deine Werte aus der ersten Aufgabe in die Gleichungen ein.

Merksatz: Nebenwinkel

Nebenwinkel ergänzen sich zu $180^\circ$.

Scheitelwinkel

• Hier fehlt noch ein Bild mit dem Winkel $\gamma$. Oder das oben stehende Bild wird dem Winkel modifiziert!!!

Aufgabe 2: Grundlagen zu Scheitelwinkeln

Nun weißt du wieder, was Nebenwinkel sind und wie du sie berechnen kannst. Wie lässt sich denn der Winkel $\gamma$ bestimmen? Wie groß ist der Winkel $\gamma$? Begründe deine Antwort in eigenen Worten.

Der Winkel $\gamma$ beträgt 25() Grad.

Versuche dein Wissen über Nebenwinkel anzuwenden. Wenn $\gamma$ ein Nebenwinkel von $\beta$ ist, wie groß ist dann $\gamma$?

Das $\alpha$ und $\beta$ Nebenwinkel sind, weiß ich schon. Da sich zwei Nebenwinkel zu $180^\circ$ ergänzen gilt für $\beta$: $\beta=180^\circ-25^\circ=155^\circ =155^\circ$. $\gamma$ ist aber auch ein Nebenwinkel von $\beta$. Deshalb ergänzen sich diese beiden Winkel auch wieder zu $180^\circ$. Also gilt für $\gamma$: $\gamma = 180^\circ -155^\circ$=25^\circ. Somit sind die Winkel $\alpha$ und $\gamma$ gleichgroß, weshalb man sie Scheitelwinkel nennt.

Merksatz: Scheitelwinkel

Scheitelwinkel sind gleich groß.

Erarbeitung

Stufen- und Wechselwinkel

Aufgabe 3: Stufen- und Wechselwinkel erkunden

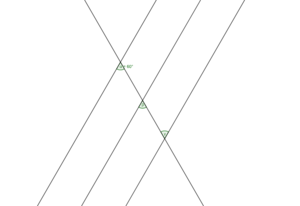
Werden zwei parallele Geraden betrachtet, die von einer dritten Gerade geschnitten werden, so entstehen verschiedene Winkel zwischen den Geraden. Wie du bereits in den vorherigen Aufgaben gemerkt hast, gibt es einige Winkel, die gleichgroß sind. Diese Winkel, die gleich groß sind, wollen wir nun genauer betrachten. Schaue dir hierfür die Folgenden GeoGebra-Applets an und probiere verschiedene Positionen der Geraden zueinander aus. Wie verhalten sich die Winkel zueinander?

Merksatz: Stufenwinkel

Schreibe den Merksatz, wie bei den Neben- und Scheitelwinkeln selber auf.

Stufenwinkel sind gleich groß().

Merksatz: Wechselwinkel

Schreibe den Merksatz, wie bei den Neben- und Scheitelwinkeln selber auf.

Wechselwinkel sind gleich groß().

(Applets von B. Lachner)

• Tipps/ Erinnerungen zum Aufklappen
• Dynamische Applets einfügen
  

Anwendung

-Bild einfügen (Fliesenmuster Rauten)

Übung

Aufgabe 4: Anwendungsaufgabe

In dieser Aufgabe kannst du nun dein Wissen über die Winkelarten anwenden. Wie groß ist der Winkel $\alpha$ im obigen Bild? Begründe deine Antwort, mit Hilfe deines Wissens über Stufen- und Wechselwinkel. Du kannst selber entscheiden, ob du zum Schrittweisen Lösen die Aufgaben 4a) und 4b) bearbeitest oder direkt die Frage beantwortest und begründest.

Aufgabe 4a): Anwendungsaufgabe

Bestimme die fehlenden Winkel!

height=500px

Aufgabe 4b): Anwendungsaufgabe

Bestimme die fehlenden Winkel!

height=500px

Sicherung

• Merksatz/ Regelhefteintrag
• Arbeitsblatt

• verschiedene Schwierigkeitsstufen zum Winkelbestimmen
• Parkettierung => Anwendungsaufgabe Leiter an Hauswand