Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Abstände von Objekten im Raum

Info

In diesem Lernpfadkapitel kannst du das Thema "Abstände von Objekten im Raum" wiederholen und vertiefen.

Wie du im Inhaltsverzeichnis siehst, gibt es drei Abschnitte: einen zum Abstand zwischen einer Ebene und einem Punkt, einen zum Abstand zwischen einer Geraden und einem Punkt und einen dritten zum Abstand zwischen zwei windschiefen Geraden. Suche dir einfach aus, was du üben möchtest. Bei jedem Abschnitt werden erst die jeweiligen Verfahren wiederholt und anschließend gibt es ein paar Aufgaben dazu, darunter sind auch Knobelaufgaben. Vorher kannst du noch die Einstiegsaufgabe machen, um deine generelle inhaltliche Vorstellung zu testen.

Dieses Thema ist nur für den LK gedacht, daher sind alle Aufgaben auch automatisch LK-Aufgaben und nicht noch jeweils mit einem ⭐ gekennzeichnet.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg und Spaß!

Einstieg

Aufgabe 1: Sachsituationen und Rechenschritte zuordnen

Zu welcher Sachsituation passen die Rechenschritte jeweils? Ordne zu.

Schiebe die Kästen an die richtige Stelle in der Tabelle. Du kannst die Kästen und Bilder vergrößern, indem du sie anklickst.

Je nachdem, bei welchem Abstandsproblem du hier noch Schwierigkeiten hattest oder was du einfach noch üben willst, kannst du dir den jeweiligen Abschnitt dieses Lernpfadkapitels anschauen.

Abstand eines Punktes von einer Ebene

Aufgabe 2: Überblick: Abstand Punkt Ebene

Abstand Punkt Ebene

Bei dieser Aufgabe kannst du einen Überblick über die Bestimmung des Abstandes zwischen einem Punkt und einer Ebene mit dem Lotfußpunktverfahren bekommen. Es geht auch um wichtige Begriffe in diesem Zusammenhang.

Fülle die Lücken mit den richtigen Wörtern. Sie werden dir angezeigt, sobald du auf eine Lücke klickst. Wenn du fertig bist, klicke auf den Haken unten rechts.

Tipp anzeigen

Die Abbildung kann dir helfen.

Merke: Abstand eines Punktes P zu einer Ebene E - Lotfußpunktverfahren

Das Vorgehen aus Aufgabe 2 hier nochmal detalliert erklärt:

1. Stelle die Gleichung für die zu $E$ orthogonale Gerade $g$ (also die Lotgerade) durch $P$ auf. Dabei kannst du als Stützvektor $\vec{p}$ und als Richtungsvektor den Normalenvektor $\vec{n}$ von $E$ nutzen: $g:\vec{x}=\vec{p}+t\cdot\vec{n}$.
2. Bestimme den Schnittpunkt $L$ von der Lotgeraden $g$ und der Ebene $E$. $L$ ist der Lotfußpunkt.
3. Bestimme den Abstand zwischen den Punkten $P$ und $L$, indem du den Betrag des Vektors $\vec{PL}$ berechnest.

Aufgabe 3: Lotfußpunktverfahren anwenden

Berechne den Abstand von der Ebene $E:2x_1+6x_2-4x_3=-32$ und dem Punkt $P(3|4|-2)$. Verwende dafür das Lotfußpunktverfahren.

Lösungsweg anzeigen

Abstand von $E:2x_1+6x_2-4x_3=-32$ und $P(3|4|-2)$:

Die Gleichung für die zu $E:2x_1+6x_2-4x_3=1$ orthogonale Gerade $l$ (also die Lotgerade) durch $P(3|4|-2)$ aufstellen:

$l:\vec{x}=\vec{p}+t\cdot\vec{n}=\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}+t\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}$.

Den Lotfußpunkt $A$ bestimmen:

$E:2(3+2t)+6(4+6t)-4(-2-4t)=32 \Rightarrow t=-1,25$

$t$ in $l$ einsetzten:

$\begin{pmatrix} 3 \\ 4 \\ -2 \end{pmatrix}-1,25\cdot\begin{pmatrix} 2 \\ 6 \\ -4 \end{pmatrix}=\begin{pmatrix} 0,5 \\ -3,5 \\ 3 \end{pmatrix}$

Der Lotfußpunkt ist $A(0,5|-3,5|3)$.

Den Abstand zwischen den Punkten $P$ und $A$ bestimmen:

$d(P;A)=|\vec{PA}|=\sqrt{(0,5-3)^2+(-3,5-4)^2+(3-(-2))^2}\approx 9,354$

$\Rightarrow d\approx 9,354$

Merke: Formel für den Abstand eines Punktes von einer Ebene

Um den Abstand zwischen einem Punkt und einer Ebene zu bestimmen, gibt es neben dem Lotfußpunktverfahren auch die Möglichkeit, diesen mit einer Formel zu berechnen.

Gegeben ist eine Ebene $E$ durch die Koordinatengleichung $E: a\cdot x_1+b\cdot x_2+c\cdot x_3=d$ und ein Punkt $P(p_1|p_2|p_3)$.

1. Stelle nun die Formel auf: Lies dazu aus der Koordinatengleichung der Ebene den Normalenvektor $\vec{n}= \begin{pmatrix} a \\ b \\ c \end{pmatrix}$ ab.

Bestimme dann die Länge des Normalenvektors: $|\vec{n}|=\sqrt{a^2+b^2+c^2}$ .

Die Formel lautet nun: $\frac {|a\cdot x_1+b\cdot x_2+c\cdot x_3-d|}{|\vec{n}|}$.

2. Berechne den Abstand, indem du die Koordinaten des Punktes $P(p_1|p_2|p_3)$ in die Formel einsetzt:

$d(P;E)=\frac {|a\cdot p_1+b\cdot p_2+c\cdot p_3-d|}{|\vec{n}|}$

Die folgenden Aufgaben kannst du entweder mit dem Lotfußpunktverfahren oder der Formel für den Abstand eines Punktes von einer Ebene lösen. Bei der Klapplösung werden jeweils beide Lösungswege aufgeführt.

Aufgabe 4: Abstand zum Schuldach

Anton und Bianca fliegen jeweils eine Drohne über das Dach ihrer Schule. Antons Drohne schwebt an der Stelle $A(3|4|-1)$ und Biancas Drohne schwebt an der Stelle $B(-1|7|4)$. Finde heraus, wer den geringeren Abstand zum Schuldach hat. Das Schuldach lässt sich durch folgende Gleichung beschreiben: $E: 8x_1-4x_2-x_3=5$. Du darfst dir aussuchen, welches Verfahren du benutzt.

Lösungsweg anzeigen

Im Folgenden wurde der Abstand mit der Formel für den Abstand eines Punktes von einer Ebene berechnet.

Der Normalenvektor der Ebene ist: $\vec{n}= \begin{pmatrix} 8 \\ -4 \\ -1 \end{pmatrix}$

Länge des Normalenvektors $\vec{n}$ bestimmen: $|\vec{n}|=\sqrt{8^2+(-4)^2+(-1)^2}=\sqrt{64+16+1}=\sqrt{81}=9$

Es folgt: $\frac {|8\cdot x_1-4\cdot x_2-1\cdot x_3-5|}{9}$.

Nun werden die Koordinaten von $A$ eingesetzt: $\frac {|8\cdot3-4\cdot4-1\cdot(-1)-5|}{9}=\frac {|24-16+1-5|}{9}=\frac {|-6|}{9}=\frac {6}{9}=\frac {2}{3}$

Die Koordinaten von $B$ können in die selbe Formel eingesetzt werden: $\frac {|8\cdot(-1)-4\cdot7-1\cdot4-5|}{9}=\frac {|-8-28-4-5|}{9}=\frac {|-45|}{9}=5$.

Damit hat die Drohne von Anton einen Abstand von $\frac{2}{3} LE$ zum Schuldach und die Drohne von Bianca einen Abstand von $5 LE$. Antons Drohne ist also näher zum Dach als Biancas Drohne.

Lösung anzeigen

Der Abstand der Drohne von Anton zum Dach beträgt $\frac{2}{3} LE$ und der Abstand von Biancas Drohne zum Dach beträgt $5 LE$. Damit ist der Abstand von Antons Drohne geringer.

Aufgabe 5: Glaspyramide - Teil 1

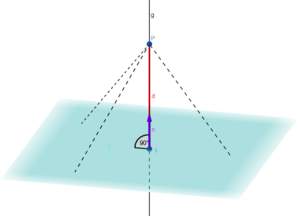
Im Innenhof des Louvre-Museums in Paris befindet sich eine große Glaspyramide. Die quadratische Grundfläche liegt in einer Ebene, die durch die Ebenengleichung $E: 2x_1+x_2+2x_3=7$ beschrieben werden kann. Die Spitze liegt im Punkt $S(4,5|9|3,5)$. Eine Längeneinheit LE im Koordinatensystem entpricht $4$m.

Welche Höhe hat die Pyramide in Metern?

Tipp

Mach dir eine Skizze. Welche Teilschritte brauchst du zur Bestimmung des Abstands? Wenn du dir unsicher bist, schau nochmal in die Merkbox oben.

Lösung anzeigen

Die Pyramide hat eine Höhe von $24$m.

Der Lösungsweg:

Die Höhe der Pyramide kann man bestimmen, indem man den Abstand zwischen der Spitze $S$ und der Ebene $E$ bestimmt.

Zuerst wird die Geradengleichung der Lotgeraden $g$ zu $E$ durch $P$ aufgestellt. Wir nehmen den Ortsvektor von $S$ als Stützvektor und den Normalenvektor von $E$ als Richtungsvektor, also: $g: \vec{x}= \begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}+ t \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}$.

Wir bestimmen den Schnittpunkt von $g$ mit $E$. Einsetzen von einem allgemeinen Punkt von $g$ in $E$ ergibt $(4,5+2t)+(9+t)+2(3,5+2t)=7$, also $t=-2$. Durch Einsetzen in die Geradengleichung $\begin{pmatrix} 4,5 \\ 9 \\ 3,5 \end{pmatrix}- 2 \cdot \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} = \begin{pmatrix} 0,5 \\ 7 \\ -0,5 \end{pmatrix}$ erhalten wir den Lotfußpunkt $L(0,5|7|-0,5)$. Dies ist gleichtzeitig der Mittelpunkt der Grundfläche der Glaspyramide.

Der Abstand zwischen $S$ und $L$ beträgt $6$LE wegen $|\vec{SL}|=\sqrt{(4,5-0,5)^2+(9-7)^2+(3,5-(-0,5))^2}=6$. Die Pyramide hat also eine Höhe von $24m$.

Aufgabe 6: Glaspyramide - Teil 2

Spitze der invertierten Glaspyramide

An einer anderen Stelle im Innenhof des Louvre befindet sich eine invertierte Glaspyramide. Das bedeutet, ihre quadratische Grundfläche liegt ebenfalls in der Ebene $E: 2x_1+x_2+2x_3=7$, ihre Spitze ist aber unterhalb des Innenhofs. Man kann sie in einem Raum unterhalb des Innenhofs besichtigen. Die Länge der vier Kanten von der Spitze bis zur jeweiligen Ecke der Grundfläche beträgt jeweils $10$m. Die Grundfläche hat $12$m lange Diagonalen, die sich im Punkt $(38 | 1 | -35)$ schneiden. In welchem Punkt $S_2$ liegt die Spitze der umgedrehten Pyramide?

Tipp 1

Zeichne eine Skizze, in der du alle bekannten Längenangaben und Punkte einträgst. Was musst du wissen, um die Position der Spitze herauszufinden?

Tipp 2

Diese Skizze der Pyramide kannst du mit deiner Maus drehen und vergrößern.

Wenn du die Höhe der Pyramide kennst, weißt du, welchen Abstand die Spitze von der Grundfläche hat. Du kennst auch schon den Mittelpunkt der Pyramide und kannst entlang des Normalenvektors von $E$ zur Spitze gelangen.

Tipp 3

Berechnung der Höhe der Pyramide

Du kannst die Höhe der Pyramide mithilfe des Satzes von Pythagoras und der Längenangaben berechnen.

Lösung anzeigen

Die Spitze der invertierten Pyramide liegt im Punkt $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$.

Hier der Lösungsweg:

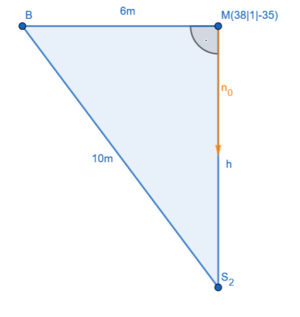
Die Höhe der Pyramide kann man mit dem Satz des Pythagoras und den Längenangaben für die Diagonale der Grundfläche und die Kanten berechnen: (siehe Zeichnung zu Tipp 3)

Es ist $\sqrt{10^2-6^2}=\sqrt{64}=8$, also beträgt die Höhe der invertierten Pyramide $8$m, was $2$LE im Koordinatensystem entspricht.

Die Spitze der umgedrehten Pyramide liegt also in einem Punkt, der einen Abstand von $2$LE zur Pyramidengrundfläche hat. Es gibt genau zwei solche Punkte, die Spitze einer "normalen" Pyramide und die Spitze der invertierten Pyramide.

Damit man die Spitze der invertierten Pyramide erhält, geht man vom Mittelpunkt $M (38 | 1 | -35)$ der Grundfläche aus $2$LE entlang der Geraden, die orthogonal zu $E$ ist, und zwar in die andere Richtung als in der Aufgabe "Glaspyramide - Teil 1". Das heißt, man geht $2$LE in die entgegengesetzte Richtung des Normalenvektors von $E$.

Es ist $|\vec{n}|=|\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}|=\sqrt{2^2+1^2+2^2}=3$, also ist $\vec{n_0}=\frac{1}{3}\begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix}=\begin{pmatrix} \frac{2}{3} \\ \frac{1}{3} \\ \frac{2}{3} \end{pmatrix}$.

Nun können wir bestimmen, in welchem Punkt $S_2$ die Spitze liegt:

Es ist $\begin{pmatrix} 38 \\ 1 \\ -35 \end{pmatrix} + (-2) \cdot \begin{pmatrix} \frac{2}{3} \\ \frac{1}{3} \\ \frac{2}{3} \end{pmatrix}=\begin{pmatrix} 36 \frac{2}{3} \\ \frac{1}{3} \\ -36 \frac{1}{3} \end{pmatrix}$, also erhält man $S_2=(36 \frac{2}{3}|\frac{1}{3}|-36 \frac{1}{3})$

Aufgabe 7: Abstand paralleler Ebenen

Gegeben ist die Ebene $E: 2x_1-3x_2+6x_3=13$. Bestimme zur Ebene $E$ zwei parallele Ebenen, die von $E$ den Abstand $5$ haben.

Tipp anzeigen

Überlege dir, welchen Normalenvektor die Ebenen haben müssen, damit sie parallel zu $E$ sind

Lösungsweg anzeigen

Die gesuchten Ebenen haben den gleichen Normalenvektor wie $E$.

Ansatz: $G:2x_1-3x_2+6x_3=h$

$P(p_1|p_2|p_3)$ sei ein Punkt der Ebene $G$. Wir wissen also, dass für $P$ die Ebenengleichung von $G$ erfüllt sein muss, also dass $2p_1-3p_2+6p_3=h$ gelten muss.

Es gilt: $d(P;E)=\frac {|2p_1-3p_2+6p_3-13|}{\sqrt{2^2+(-3)^2+6^2}}=\frac{|2p_1-3p_2+6p_3-13|}{\sqrt{49}}=\frac {|2p_1-3p_2+6p_3-13|}{7}=\frac{|h-13|}{7}$.

$d(P;E)=5$ nach Aufgabenstellung. Daher gilt: $\frac{h-13}{7}=5$ oder $\frac{h-13}{7}=-5$.

Stelle nun beide Gleichungen nach $h$ um.

Es folgt: $h_1=48$ und $h_2=-22$.

Dies wird nun in die Ebenengleichung von $G$ eingesetzt:

$G_1:2x_1-3x_2+6x_3=48$

$G_2:2x_1-3x_2+6x_3=-22$

$G_1$ und $G_2$ haben nun beide den Abstand $5$ zur Ebene $E$.

Lösung anzeigen

$G_1:2x_1-3x_2+6x_3=48$ und

$G_2:2x_1-3x_2+6x_3=-22$

haben beide den Abstand $5$ zu $E$.

Abstand eines Punktes von einer Geraden

Aufgabe 8: Grafische Darstellung: Abstand eines Punktes von einer Geraden

Bewege den Punkt $Q$ auf der Geraden $g$, um dir den jeweiligen Abstand zwischen den Punkten $P$ und $Q$ anzeigen zu lassen. Rechts neben der Geraden siehst du, wie groß der Abstand jeweils ist.

Wann ist der Abstand vom Punkt $P$ zur Geraden $g$ am kleinsten?

Wie groß ist der Winkel zwischen $g$ und der Geraden durch $P$ und $Q$? Wie nennt man $Q$ dann?

Versuche es zuerst ohne die Hilfslinie. Überprüfe dich dann selbst.

Lösung anzeigen

Der Abstand $d(P;Q)$ ist am kleinsten, wenn $\vec{PQ}$ orthogonal zu $g$ ist. Dies kannst du sehen, wenn du dir die Hilfslinie anzeigen lässt.

Dann nennt man den Punkt $Q$ den Lotfußpunkt von $P$ auf $g$.

Merke: Der Abstand eines Punktes zu einer Geraden

Der Abstand eines Punktes $P$ zu einer Geraden $g$ ist der Abstand von $P$ und $L$, wobei $L$ der Lotfußpunkt von $P$ auf $g$ ist.

Für die Bestimmung des Abstandes $d(P,g)=d(P,L)$ gibt es zwei verschiedene Verfahren:

Verfahren Hilfsebene

1. Stelle eine Hilfsebene $H$ (in Koordinatenform) auf, die den Punkt $P$ enthält und orthogonal zu zu $g$ ist. Dafür kannst du als Stützvektor $\vec{p}$ und als Normalenvektor den Richtungsvektor von $g$ nehmen.
2. Bestimme den Schnittpunkt $L$ von $g$ und $H$ durch Einsetzen.
3. Berechne den Abstand $d(P;g)=d(P;L)$.

Verfahren Orthogonalität

1. Bestimme einen allgmeinen Verbindungsvektor von $P$ zu einem beliebigen Geradenpunkt $L$ in Abhängigkeit vom Geradenparameter $r$.
2. Wähle $r$ so, dass der Verbindungsvektor orthogonal zum Richtungsvektor der Geraden $g$ ist.
3. Berechne nun den Abstand $d(P;g)=d(P;L)$.

Aufgabe 9: Lichterkette

Für ein Stadtfest soll von der Dachspitze $P(-2|3|10)$ eines Restaurants eine Lichterkette auf kürzestem Weg zur nahen Uferlinie des Kanals $g:\vec{x}=\begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+r\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}$ gespannt werden. Eine Längeneinheit im Koordinatensystem entspricht $1$ m.

Berechne die Mindestlänge der Lichterkette auf Meter gerundet.

Lösungsweg anzeigen

1. Stelle die Hilfsebene $H$ in Koordinatenform auf:

$-4x_1+3x_2+2x_3=37, da \begin{pmatrix} -2 \\ 3 \\ 10 \end{pmatrix}\ast\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=37$

2. Schnittpunkt von $g$ und $H$ bestimmen: $-4\cdot(1-4r)+3\cdot(2+3r)+2\cdot(3+2r)=37 \Leftrightarrow -4+16r+6+9r+6+4r=37 \Leftrightarrow 8+29r=37 \Leftrightarrow 29r=29 \Leftrightarrow r=1$

3. $r$ in $g$ einsetzten, um $L$ zu bestimmen:

$\vec{OL}= \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}+1\cdot\begin{pmatrix} -4 \\ 3 \\ 2 \end{pmatrix}=\begin{pmatrix} -3 \\ 5 \\ 5 \end{pmatrix}$ $\Rightarrow L(-3|5|5)$

4. Abstand $d(P;L)$ bestimmen: $d(P;L)=\sqrt{(-3-(-2))^2+(5-3)^2+(5+10)^2}=\sqrt{30}\approx 5,477$

Die Lichterkette muss mindestens $5,48$ Meter lang sein.

Lösung anzeigen

Die Lichterkette muss mindestens $5,48$ Meter lang sein.

Aufgabe 10: Die richtige Reihenfolge

Im Folgenden wurde der Abstand von $A(3|9|-2)$ und $g:\vec{x}=\begin{pmatrix} 9 \\ -3 \\ 2 \end{pmatrix}+s\cdot\begin{pmatrix} 4 \\ -5 \\ -7 \end{pmatrix}$ bestimmt. Bringe die einzelnen Schritte in die richtige Reihenfolge.

Aufgabe 11: Dreieck

Betrachte das Dreieck $DBC$. Es sind die Punkte $B(2|8|1)$ und $C(0,5|3,5|7)$ gegeben, durch sie verläuft die Gerade $i$. Der Punkt $D$ liegt auf der zu $i$ parallelen Geraden $j:\vec{x}= \begin{pmatrix} 1 \\ 1 \\ 2 \end{pmatrix}+t\cdot\begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}$.

a) Stimmt die Behauptung "Der Flächeninhalt des Dreiecks $DBC$ ändert sich, je nachdem wo $D$ auf der Geraden $j$ liegt"? Wenn ja, warum? Wenn nein, warum nicht?

Du kannst mit der Maus den Punkt $D$ verschieben.

Tipp zu a)anzeigen

Überlege dir, wie man den Flächinhalt eines Dreiecks allgemein berechnet. Wie ändert sich die Höhe des Dreiecks, wenn man $D$ verschiebt?

Lösung zu a) anzeigen

Die Behauptung stimmt nicht. Den Flächeninhalt Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}} eines Dreiecks kann man bekanntermaßen mit der Formel Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h} berechnen, wobei $g$ die Länge der Grundseite ist.

In dieser Aufgabe bleibt der Abstand $d(D;i)$ immer gleich, da sich $D$ auf einer zu $i$ parallelen Geraden "bewegt". Also ist die Höhe $h$ all dieser Dreiecke gleich. Deshalb ändert sich auch der Flächeninhalt Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h} nicht.

b) Bestimme den Flächeninhalt des Dreicks $DBC$.

Tipp zu b)anzeigen

Überlege dir, welche Abstände du berechnen musst, um den Flächeninhalt bestimmen zu können.

Lösung anzeigen

Der Flächeninhalt des Dreiecks beträgt ungefähr $19,12$ Flächeneinheiten.

Ein möglicher Lösungsweg: Wir bestimmen zunächst die Länge $g$ der Grundseite: Es $|\vec{BC}|=\sqrt{(2-0,5)^2+(8-3,5)^2+(1-7)^2}=\sqrt{58,5}$.

Nun bestimmen wir die Höhe $h$, also den Abstand der parallelen Geraden $i$ und $j$ mithilfe des Verbindungsvektors von $B$ zur Geraden $j$.(Da die Geraden parallel sind, ist es natürlich egal, welche der Geraden und welchen Punkt auf der anderen Geraden man nimmt. Ihr könntet ebenso mit dem anderen Verfahren, also mit einer Hilfsebene arbeiten):

Der Punkt $L_t=(1+t|1+3t|2-4t)$ ist ein allgemeiner Punkt auf $j$. Ein allgemeiner Verbindungsvektor zwischen $B$ und $j$ ist also gegeben durch $\vec{BL_t}=\begin{pmatrix} (1+t)-2 \\ (1+3t)-8 \\ (2-4t)-1 \end{pmatrix}=\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}$.

Damit $\vec{BL_t}$ orthogonal zum Richtungsvektor von $j$ ist, muss gelten: $\begin{pmatrix} -1+t \\ -7+3t \\ 1-4t \end{pmatrix}\ast \begin{pmatrix} 1 \\ 3 \\ -4 \end{pmatrix}=0$ bzw. $(t-1)\cdot 1+(-7+3t)\cdot 3 + (1-4t) \cdot (-4)=0$. Es folgt $t=1$, also ist der Verbindungsvektor für $L(2|4|-2)$ am kürzesten. Somit ist $h=d(B;j)=|\vec{BL}|=\sqrt{(2-2)^2+(4-8)^2+(-2-1)^2}=\sqrt{25}=5$.

Der Flächeninhalt des Dreiecks beträgt also Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle A_\{text{DBC}}=\frac{1}{2}\cdot g \cdot h=\frac{1}{2}\cdot \sqrt{58,5} \cdot 5\approx 19,12} Flächeneinheiten.

Abstand zweier windschiefer Geraden

Aufgabe 12: Die kürzeste Verbindungsstrecke zwischen windschiefen Geraden

Verschiebe die Punkte $G$ und $H$ so, dass $\overline{GH}$ die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden $g$ und $h$ ist. Du kannst die Grafik mit deiner Maus drehen, um die Geraden aus anderen Perspektiven zu betrachten.

Lösung anzeigen

Damit $\overline{GH}$ die kürzeste Verbindungsstrecke zwischen den windschiefen Geraden $g$ und $h$ ist, müssen beide Winkel $90^{\circ}$ groß sein.

Merke: Der Abstand windschiefer Geraden

Der Abstand zweier windschiefer Geraden $g$ und $h$ ist die kürzeste Verbindung zwischen einem Punkt der Geraden $g$ und einem Punkt der Geraden $h$. Diese kürzeste Verbindungsstrecke $\overline{GH}$ zwischen den beiden Geraden ist sowohl orthogonal zu $g$ als auch orthogonal zu $h$ und heißt gemeinsames Lot der windschiefen Geraden $g$ und $h$.

Für die Bestimmung des Abstandes $d(g;h)$ berechnet man also die Länge des gemeinsamen Lotes der Geraden. Dafür gibt es wieder verschiedene Möglichkeiten. Hier werden zwei Verfahren noch einmal zusammengefasst: Seien $g: \vec{x}=\vec{p}+s\cdot \vec{u}$ und $h: \vec{x}=\vec{q}+t\cdot \vec{v}$ die windschiefen Geraden.

Verfahren Gemeinsames Lot

1. Bestimme die Geradenpunkte $G$ und $H$ in Abhängigkeit von dem jeweiligen Geradenparameter.
2. Stelle den Verbindungsvektor $\vec{G_s H_t}$ in Abhängigkeit von den Geradenparametern auf.
3. Bestimme nun die Parameter $s$ und $t$ so, dass der Verbindungsvektor $\vec{G_s H_t}$ orthogonal zu den Richtungsvektoren von $g$ und $h$ ist. Du löst also das lineare Gleichungssystem mit den beiden Gleichungen $\vec{G_s H_t}\ast \vec{u} =0$ und $\vec{G_s H_t}\ast \vec{v} =0$.
4. Mit diesen Parametern erhältst du die Lotfußpunkte $G$ und $H$ und kannst den Abstand $d(g;h)=d(G;H)$ bestimmen.

Verfahren Hilfsebene

Es gibt eine Ebene $E$, sodass $g$ in $E$ liegt und $h$ parallel zu $E$ ist. Für diese Ebene $E$ ist dann der Abstand zwischen den Geraden $d(g,h)$ gleich dem Abstand zwischen $E$ und einem beliebigen Punkt $H$ auf $h$. Jeder Normalenvektor von dieser Ebene $E$ ist orthogonal zu den Richtungsvektoren von $g$ und $h$.

1. Bestimme aus den Gleichungen $\vec{u}\ast\vec{n}=0$ und $\vec{v}\ast\vec{n}=0$ einen Normalenvektor.
2. Stelle die Normalengleichung $(\vec{x}-\vec{p})\ast\vec{n}=0$ der Ebene $E$ auf.
3. Bestimme mit der Formel für den Abstand eines Punktes von einer Ebene oder dem Lotfußpunktverfahren (siehe Abschnitt Abstand Punkt Ebene) den Abstand $d(E;H)=d(g;h)$.

Aufgabe 13: Maulwurfstunnel

Zwei Maulwürfe graben Tunnel mit einem Durchmesser von jeweils $5$cm.

Der erste Maulwurf gräbt entlang der Geraden $g:\vec{x}=\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}+s\cdot \begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}$ und der zweite entlang der Geraden $h:\vec{x}=\begin{pmatrix} 6 \\ 6 \\ 18 \end{pmatrix}+t\cdot \begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}$ wobei diese Geraden jeweils in der Mitte des Tunnels liegen.

Die Geraden schneiden sich nicht, aber ihre Tunnel sind nur stabil, wenn überall mindestens $15$cm Erde dazwischen sind. Eine Längeneinheit im Koordinatensystem entspricht $1$cm. Wird das Tunnelsystem halten?

Tipp anzeigen

Wenn die kleinste Entfernung, also der Abstand zwischen den Geraden groß genug ist, ist auch an allen anderen Stellen genug Erde zwischen den Tunneln. Überlege dir, welchen Abstand die Geraden voneinander haben müssten, damit die Tunnel nicht einstürzen. Berechne dann den Abstand zwischen den Geraden mit einem Verfahren deiner Wahl.

Möglichen Lösungsweg anzeigen

Da die Tunnel einen Radius von $2,5$cm haben und die Geraden in dem Modell in der Mitte der jeweiligen Tunnel liegen, müssen die Geraden mindestens einen Abstand von $2,5+15+2,5=20$ haben, damit die Tunnel nicht einstürzen.

Wir bestimmen den Abstand zwischen den Geraden mithilfe einer Hilfsebene $E$, die parallel zur Geraden $h$ ist und in der die Gerade $g$ liegt. Für den Normalenvektor $\vec{n}$ muss gelten: $\begin{pmatrix} -3 \\ 0 \\ 2 \end{pmatrix}\ast \vec{n}=0$ und $\begin{pmatrix} 3 \\ -4 \\ 1 \end{pmatrix}\ast \vec{n}=0$. Es folgt $n_1=\frac{2}{3} n_3$ und $n_2=\frac{3}{4} n_3$. Also ist $\vec{n}=\begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix}$ ein Normalenvektor von $E$. Die Normalenform von $E$ lautet nun $E:[\vec{x}-\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}]\cdot \begin{pmatrix} \frac{2}{3} \\ \frac{3}{4} \\ 1 \end{pmatrix} =0$. Nehme den Punkt $H(6|6|18)$ auf der Geraden $h$. Da der Abstand zwischen den Geraden gleich dem Abstand zwischen der Ebene $E$ und einem beliebigen Punkt auf der zu $E$ parallelen Geraden $h$ ist, erhält man nun mit der Formel für den Abstand eines Punktes von einer Ebene $d(g;h)=d(E;H)=\frac{|\frac{2}{3}\cdot 6+\frac{3}{4}\cdot 6+18-(\frac{2}{3}\cdot 1+\frac{3}{4}\cdot 1+1)|}{\sqrt{(\frac{2}{3}^2+(\frac{3}{4})^2+1^2}}=17.$

Die Geraden haben also einen kleineren Abstand als $20$LE. Das heißt, die Tunnel sind nicht überall mindestens $15$cm voneinander entfernt und sie werden einstürzen.

Die einzige Lösung für die Maulwürfe ist es, an der kritischen Stelle eine gemeinsame Höhle zu bauen. :)

Lösung anzeigen

Die Geraden haben einen Abstand von $17LE$. Zwischen den Tunneln sind also an einer Stelle nur $12cm$ Erde und sie werden einstürzen.

Dann bauen die beiden Maulwürfe an der kritischen Stelle einfach eine gemeinsame Höhle. :)

Aufgabe 14: Geradenpaare, Abstände und Lotfußpunkte zuordnen

Bei dieser Aufgabe gibt es drei Geradenpaare $g$ und $h$, die jeweils windschief zueinander liegen. Schiebe zuerst die Geradenpaare auf das Feld mit der entsprechenden Nummer. Ordne ihnen dann die jeweiligen Lotfußpunkte $G$ und $H$ sowie den entsprechenden Abstand zwischen den Geraden zu. Ein paar Zettel bleiben übrig, diese schiebst du auf das letzte Feld. Du kannst die Zettel vergrößern, indem du sie anklickst.

Tipp: Durch genaue Überlegungen, Rückwärtsrechnen und mithilfe von Skizzen kann man manchmal schnell erkennen, was zusammengehört, ohne alle Schritte des Verfahrens durchzugehen!

Wenn du auf den Haken klickst, kannst du überprüfen, ob du richtig zugeordnet hast.

Möglichen Lösungsweg für 1. anzeigen

Du kannst natürlich auch mit dem Verfahren die beiden Lotfußpunkte bestimmen. Hier kannst du dir aber "rückwärts" schneller überlegen, was die Lotfußpunkte sind: Durch Einsetzen erkennt man, dass $G(0|2|0)$ und $H(-1|0|-2)$ auf der jeweiligen Gerade liegen. Der Verbindungsvektor $\vec{GH}=\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}$ ist wegen $\begin{pmatrix} 0 \\ -1 \\ 1 \end{pmatrix}\ast\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}=0$ und $\begin{pmatrix} 1 \\ -\frac{1}{2} \\ 0 \end{pmatrix}\ast\begin{pmatrix} -1 \\ -2 \\ -2 \end{pmatrix}=0$ orthogonal zu $g$ und $h$. Also sind $G(0|2|0)$ und $H(-1|0|-2)$ die Lotfußpunkte und es ist $d(g;h)=|\vec{GH}|=\sqrt{(-1)^2+(-2)^2+(-2)^2}=3$.

Möglichen Lösungsweg für 2. anzeigen

Da $g$ entlang der $x_1$-Achse verläuft, liegt diese Gerade auch in der $x_1$$x_2$-Ebene.

Der Vektor $\begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}$ ist ein möglicher Stützvektor für eine Geradengleichung von $h$, denn $h$ veräuft durch den Punkt $(0|2|1)$. Da die Gerade $h$ parallel zur $x_2$-Achse ist und der Eintrag des Stützvektors $\begin{pmatrix} 0 \\ 2 \\ 1 \end{pmatrix}$ in der $x_3$-Koordinate $1$ ist, ist $h$ parallel zur $x_1$$x_2$-Ebene und alle Punkte auf der Geraden $h$ haben die $x_3$-Koordinate $1$.

Also kann man den Abstand der Geraden direkt an der $x_3$-Koordinate des Stützvektors der Geraden $h$ ablesen: $d(g;h)=|1|=1$.

Außerdem liegt $G(0|0|0)$ auf $g$ und $H(0|0|1)$ auf $h$ und der Verbindungsvektor $\vec{GH}=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ ist orthogonal zu den Richtungsvektoren $\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}$ und $\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}$ beider Geraden. Also sind diese beiden Punkte die Lotfußpunkte. Das gemeinsame Lot liegt insbesondere auf der $x_3$-Achse. Dies kann man daran erkennen, dass $g$ entlang der $x_1$-Achse verläuft und $h$ parallel zur $x_2$-Achse und nicht in $x_1$-Richtung verschoben ist (der Stützvektor von $h$ hat die $x_1$-Koordinate $0$). Beide Geraden schneiden also die $x_3$-Achse und sind parallel zur $x_1$$x_2$-Ebene bzw. liegen in dieser Ebene.

Möglichen Lösungsweg für 3. anzeigen

Da der Richtungsvektor von $h$ im Eintrag der $x_2$-Koordinate $0$ ist, ist $h$ parallel zur $x_1$-$x_3$-Ebene. $g$ liegt in der $x_1$-$x_3$-Ebene. (Da die Richtungsvektoren von $g$ und $h$ linear unabhängig sind, sind die Geraden nicht parallel zueinander, was aber ja auch schon in der Aufgabenstellung gesagt wurde.) Also kann man den Abstand der Geraden direkt am Unterschied der $x_2$-Koordinaten der Stützvektoren der beiden Geraden ablesen: $d(g;h)=|2-0|=2$. Da man aber nicht genau weiß, wo $g$ liegt (man kennt nur den Richtungsvektor), kann man auch nicht sagen, wo genau die Lotfußpunkte liegen.