Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum
Wiederholung von Punkten und Vektoren
Das dreidimensionale Koordinatensystem
{{Box|1 = Übung 1: Lückentext Körper|2= Ziehe die korrekten Wörter in die jeweiligen Lücken.
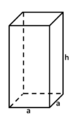
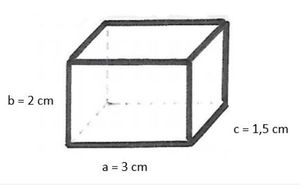
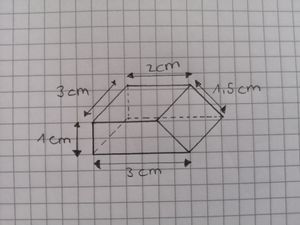
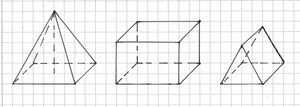
Im Schrägbild nimmt man Körper auf der ebenen Fläche räumlich wahr.
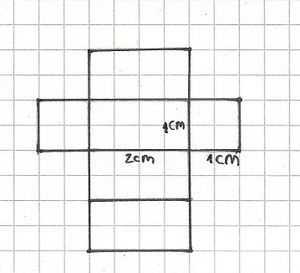
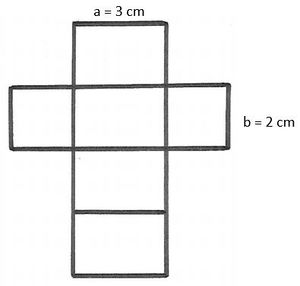
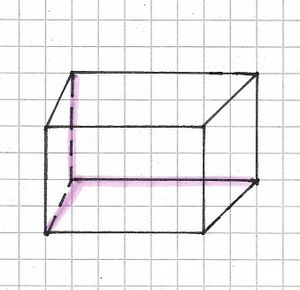
Die Vorderseite des Quaders solltest du in Originalgröße zeichnen. Wenn der Quader eine Länge von 8 cm und eine Höhe von 2 cm hat, ist das Rechteck, das du als seine Vorderseite zeichnest, 8 cm breit und 2 cm hoch.
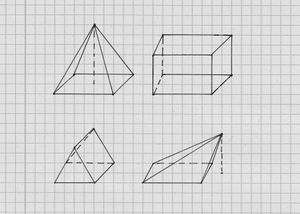
Ein Würfel hat 8 Ecken, 6 Flächen und 12 Kanten. Außerdem sind alle Kanten gleich lang und alle Flächen quadratisch. Auch sind die Flächen gleich groß.
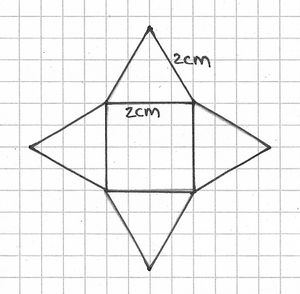
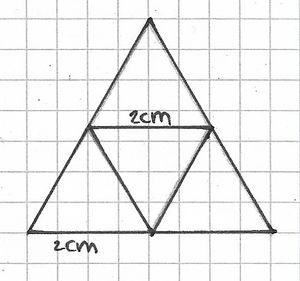
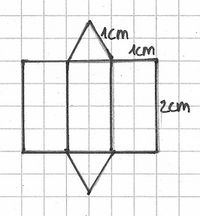
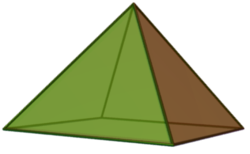
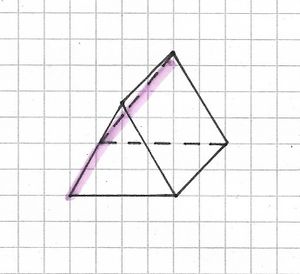
Eine Pyramide ist ein Körper, der aus einem Vieleck (Drei-, Vier-, Fünfeck usw.) und mehreren Dreiecken besteht. Das Vieleck bildet die Grundfläche und die Dreiecke die Mantelfläche der Pyramide.
|Farbe=#F19D50|3= Arbeitsmethode}}
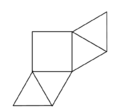
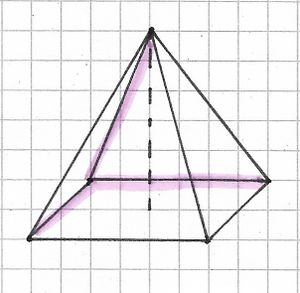
{{Box|Übung 2: Punkte im Koordinatensystem|An welchen Koordinaten liegen die Ecken des angegebenen Tetraeders?
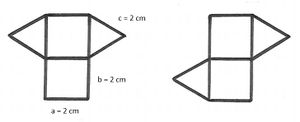
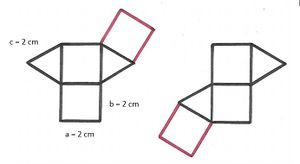
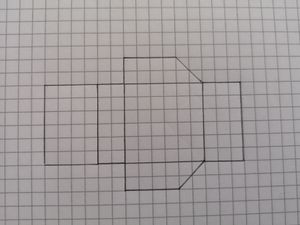
Schrägbilder und Netze
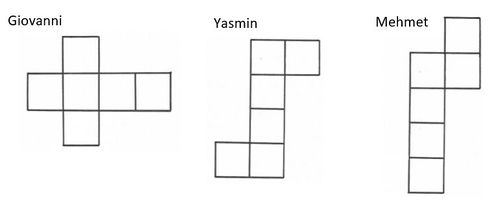
Übungen: Netze
Übungen: Schrägbilder
Unmögliche Figuren
Übungen: unmögliche Figuren
Quellen
- https://learnattack.de/mathematik/koerpernetz-und-schraegbild-von-koerpern#video-was-sind-schr%C3%A4gbild-und-netz-eines-k%C3%B6rpers
- https://www.geogebra.org/m/a7wZdw5C#material/Qf9yn4sG
- https://www.geogebra.org/m/SQm8Xq3y
- https://www.geogebra.org/m/ab93zf9g
- https://www.geogebra.org/m/nc7KHTJt
- https://www.geogebra.org/material/show/id/ab93zf9g#
- https://www.geogebra.org/material/show/id/Z57aCNpm#
- https://www.youtube.com/watch?v=dvSD1EAlAUQ
- https://www.klippert-medien.de/media/ntx/klippert/sample/09108DA5_Musterseite.pdf
- https://nl.wikipedia.org/wiki/Onmogelijke_figuur#/media/Bestand:Blivet.png
- https://de.wikipedia.org/wiki/Unm%C3%B6gliche_Figur#/media/Datei:Impossible_staircase.svg
- https://de.wikipedia.org/wiki/Penrose-Dreieck#/media/Datei:Deutsches_Technikmuseum_Berlin_February_2008_0005.JPG
- https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Reutersv%C3%A4rd%E2%80%99s_triangle.svg
- https://es.wikipedia.org/wiki/Objeto_imposible#/media/Archivo:Impossible_cube_illusion_angle.svg
Geogebra Applets
Pyramidenaufgabe Übung 6 Lösung

Netzaufgabe Übung 4 a Tipp

Netzaufgabe Übung 4 b Tipp

Netzaufgabe Übung 4 c Tipp

Netzaufgabe Übung 4 d Tipp

Wir definieren zwei Rechenoperationen für Vektoren: das Bilden des Vielfachen und der Summe. Die Vektoraddition bezeichnet das bilden der Summe zweier Vektoren gleichen Typs, das heißt dass die beiden Vektoren gleich viele Komponenten haben. Man bildet die Summe, indem man die Einträge der Vektoren komponentenweise addiert. Wir können uns die Addition von Vektoren als ein „Aneinanderlegen“ von zwei Strecken von ggf. verschiedener Länge vorstellen. Nennen wir und Vektoren. Wir deuten diese als Pfeile und addieren sie, das heißt wir legen sie hintereinander, sodass der Anfang von und die „Spitze“ von übereinstimmen. Ein derartiges Verhalten von Pfeilen ist aus der Physik bekannt. Dort werden oftmals Kräfte und Geschwindigkeiten mit Pfeilen dargestellt. Man kann am Ende zur Addition sagen, dass das Bilden der Summe zweier Vektoren als Hintereinander-Ausführen der durch und dargestellten Verschiebungen gesehen werden kann.
Das Bilden des Vielfachen eines Vektors wird auch als Multiplikation mit einem Skalar bezeichnet. Wir nennen unseren Vektor wieder und das Skalar bezeichnen wir mit . Von jedem Vektor kann das -Fache gebildet werden, indem alle Komponenten von mit multipliziert werden. Ist so wird der „Pfeil“ von um den Faktor aufgeblasen (falls ) oder geschrumpft (falls ). Ist , so erhält der Pfeil, der um den Faktor aufgeblasen oder geschrumpft wird, noch eine Richtungsumkehrung und wird zum Gegenvektor.
Wir nennen zwei Vektoren kollinear (oder parallel), wenn einer der Vektoren ein Vielfaches des anderen ist. Mit anderen Worten: Wenn und zwei verschiedene Vektoren sind, so sind sie parallel/kollinear zueinander, falls ein Skalar existiert, sodass gilt: . Dabei ist es egal, ob die beiden Vektoren in unterschiedliche Richtungen zeigen oder nicht.