SEITE IM AUFBAU!
12-Knoten-Seil
Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Was beobachtest du?
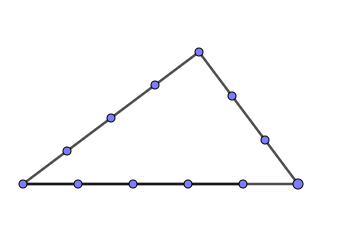
Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.
Applet von Pöchtrager
Was hat das mit dem Satz des Pythagoras zu tun?
Applet von Pöchtrager
Satz des Pythagoras
In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrat über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras
a² + b² = c².
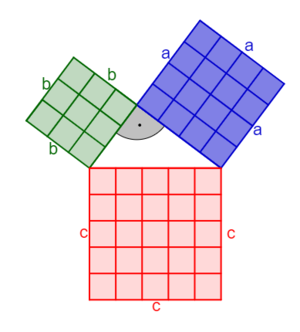
Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.
Applet von Pöchtrager
Zerlegungsbeweise
Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!
Beweis Nr. 1:
Applet von J. Mil
Beweis Nr. 2:
Applet von B.Lachner
Beweis Nr. 3:
Applet von Pöchtrager
Übungen (GeoGebra-Applets von Pöchtrager)
Pythagorasbaum:
(Appelt von Pöchtrager)















