Digitale Werkzeuge in der Schule/Fit für VERA-8/Einfache Gleichungen

Info

In diesem Lernpfadkapitel lernst du das Wichtigste zum Thema Einfache Gleichungen. Am Anfang des Kapitels kannst du die wichtigsten Begriffe wiederholen und dann dein Wissen in verschiedenen Aufgaben anwenden. Am Ende dieses Kapitels solltest du ...

• ... wissen, was eine Variable, ein Term, eine Gleichung und die Lösungsmenge sind.
• ... vorgegebene Gleichungen nach der Variable auflösen, die Probe durchführen und die Lösungsmenge angeben können.
• ... kurze Zahlenrätsel in Gleichungen überführen und lösen können.
• ... Gleichungen aus Aufgaben im Sachzusammenhang aufstellen und lösen können.

Zum Anfang des Kapitels sind die Aufgaben leichter und werden zum Ende hin schwerer. Wir unterscheiden folgende Aufgabentypen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Viel Erfolg!

Die wichtigsten Definitionen und Begriffe in diesem Kapitel

Die wichtigsten Begriffe, die du zum Bearbeiten der Aufgaben benötigst, werden hier in Merkkästen erklärt. Sollten dir diese Begriffe schon vertraut sein, kannst du diesen Teil überspringen und mit den Aufgaben starten. Falls du während der Bearbeitung einer Aufgabe unsicher bist, kannst du immer in diesen Abschnitt zurückkehren und dir die Merkkästen erneut durchlesen.

Definitionen und Begriffe für Einfache Gleichungen

Variable

Variablen sind sogenannte Platzhalter in Gleichungen. Für diese Platzhalter können beliebige Zahlen eingesetzt werden, für die die Gleichung korrekt bleibt. Die Platzhalter sind in den meisten Fällen Buchstaben, wie z. B. $x$, $b$, $a$, $h$, ...

Term

Ein Term ist eine Kombination aus Variablen, Zahlen, mathematischen Verknüpfungen ($+$,$-$,...) und Klammern.

Beispiele sind:

$x+y$ oder

$d\cdot (3+5x)$ oder

$3+4-2$.

Gleichung

Eine Gleichung ist ein mathematischer Ausdruck, der aus zwei Termen besteht, die durch ein „$=$“–Zeichen miteinander verbunden sind.

Lösungsmenge

Um eine Gleichung zu lösen, müssen alle Zahlen gefunden werden, für die beim Einsetzen die Gleichung erfüllt ist. Die Menge aller Lösungen wird Lösungsmenge $\mathbb{L}$ genannt.

Beispiel:

Die Gleichung $5-x=3$ lässt sich leicht lösen: $x=2$. Dann erhalten wir die Löungsmenge $\mathbb{L}=\{2\}$.

Alles in der Waage

Aufgabe 1: Waagschalenvergleich

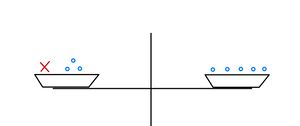
Unten kannst du eine Waage sehen. Anfangs ist die Waage für einen festen Wert für $x$ unausgeglichen. Durch das Hinzufügen von Kugeln oder $x$ auf beiden Seiten kann ein Gleichgewicht erzielt werden. Dabei kann durch Probieren herausgefunden werden, welchen Wert $x$ hat. Klickst du auf "neues $x$", wird ein neuer Wert für $x$ bestimmt.

a) Bringe die Waage ins Gleichgewicht. Wie gehst du vor? Wiederhole die Aufgabe für verschiedene Werte von $x$, indem du auf "neues $x$" klickst.

Die Waage kann ins Gleichgewicht gebracht werden, indem auf der rechten Seite nach und nach Kugeln hinzugefügt oder entfernt werden bis die Waage ausgeglichen ist. Dann kannst du abzählen, wie viele Kugeln mehr auf der Seite ohne $x$ sind. Diese Zahl ist das gesuchte $x$.

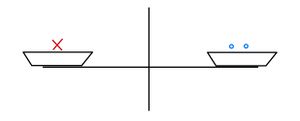
b) Die Waage steht immer noch im Gleichgewicht. Füge nun ein [zwei] weitere $x$ zur linken Waagschale hinzu. Wie gehst du jetzt vor?

Fügst du ein [zwei] weiteres $x$ zur linken Seite hinzu, so müssen doppelt [dreimal] so viele Kugeln zur rechten Seite hinzugefügt werden wie vorher. Wurden also bei einem $x$ auf der linken Waagschale nur drei Kugeln hinzugefügt, sind es bei zwei $x$ sechs Kugeln.

c) Bringe die Waage ins Gleichgewicht. Nimm dann auf beiden Seiten der Waage gleich viele Kugeln weg. Was kannst du beobachten?

Werden auf beiden Seiten der Waage gleich viele Kugeln entfernt, bleibt die Waage im Gleichgewicht.

Gleichungen lösen

Aufgabe 2: Lösungsmenge bestimmen

Bestimme die Lösungsmenge der Gleichung. Führe, wenn möglich, eine Probe durch. Denke daran: Eine Probe kann nur durchgeführt werden, wenn es mindestens eine Lösung für die Gleichung gibt.

Beispiel 1: Richtig Gleichungen lösen

Um eine Gleichung zu lösen, wird sie zunächst nach der Variable aufgelöst. Diese Variable soll am Ende isoliert, d.h. alleine, auf einer Seite der Gleichung stehen. Wir schauen uns ein Beispiel an:

$3y+5=y+35$.

Um diese Gleichung zu lösen, bringen wir zunächst alle $y$ auf eine Seite der Gleichung.

$\begin{align} && 3y+5&=y+35 & &\mid -y\\ \Leftrightarrow & & 2y+5&=35\\ \end{align}$

Jetzt können wir wie gewohnt nach $y$ auflösen.

$\begin{align} & & 2y+5&=35 & &\mid -5\\ \Leftrightarrow & & 2y&=30 & &\mid :2\\ \Leftrightarrow & & y&=15 \end{align}$

Probe:

$\begin{align} & &(3\cdot 15)+5&=15+35\\ \Leftrightarrow & & 45+5 &=50\\ \Leftrightarrow & & 50 &=50 \end{align}$

Wir erhalten also die Lösungsmenge $\mathbb{L}=\{15\}$.

Wenn du nicht mehr weißt, was die Lösungsmenge ist, schau bei den Definitionen nach.

a) Löse die Gleichung anschaulich mittels Skizzen von Waagen in deinem Heft: $x+3=5$

Überlege dir, wie die Waage im Gleichgewicht aussieht.

Beide Seiten der Gleichung sind gleichwertig. Also ist die Waage im Gleichgewicht.

Waage im Gleichgewicht

Die Waage bleibt im Gleichgewicht wenn gleich viele Kugeln auf beiden Seiten ergänzt oder entfernt werden. Wir entfernen jeweils drei Kugeln.

Waage nach Durchführung einer Umformung

$\begin{align} & & x+3 &=5 & &\mid -3\\ \Leftrightarrow & & x &=2 \end{align}$

Probe:

$\begin{align} & & 2+3 &=5 \\ \Leftrightarrow & & 5 &=5 \end{align}$

Wir erhalten die Lösungsmenge $\mathbb{L}=\{2\}$.

b) $a-64=5$

Versuche die Gleichung so umzustellen, dass auf der einen Seite des Gleichheitszeichens nur noch das $a$ steht.

$\begin{align} & & a-64 &=5 & &\mid +64\\ \Leftrightarrow & & a &=69 \\ & & \mathbb{L}=\{69\} \end{align}$

Probe:

$\begin{align} & & 69-64 &=5 \\ \Leftrightarrow & & 69-64 &=5\\ \Leftrightarrow & & 5 &=5 \end{align}$

c) $3x+7=16$

Versuche zunächst die Gleichung so umzustellen, dass auf der einen Seite nur noch das $x$ mit dem Faktor steht.

$\begin{align} & & 3x+7&=16 & &\mid -7\\ \Leftrightarrow & & 3x &=9 & &\mid :3\\ \Leftrightarrow & & x &=3\\ & & \mathbb{L}=\{3\} \end{align}$

Probe:

$\begin{align} & & 3\cdot 3+7&=16\\ \Leftrightarrow & & 9+7 &=16\\ \Leftrightarrow & & 16 &=16 \end{align}$

d) $d\cdot (d-5)=0$

Überlege dir, was für zwei Faktoren gilt, deren Produkt $0$ ist.

Ein Produkt ist dann $0$, wenn einer der Faktoren $0$ ist. Deshalb kann man die Aufgabe so lösen:

$\begin{align} & & d\cdot (d-5)&=0\\ \Leftrightarrow & & d=0 &\text{ oder } d-5=0\\ \Leftrightarrow & & d=0 &\text{ oder } d=5\\ & & \mathbb{L}=\{0,5\} \end{align}$

Probe:

$\begin{align} & & 0\cdot (0-5)&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

$\begin{align} & & 5\cdot (5-5)&=0\\ \Leftrightarrow & & 5\cdot 0&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

e) $4(x+1)-4x-5=1$

Löse zuerst die Klammer auf.

$\begin{align} & & 4(x+1)-4x-5 &=1\\ \Leftrightarrow & & 4x+4-4x-5 &=1\\ \Leftrightarrow & & 4x-4x+4-5 &=1\\ \Leftrightarrow & & -1 &=1 \end{align}$

Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: $\mathbb{L}=\{\}$. Hier ist keine Probe durch Einsetzen möglich, weil die Lösungsmenge leer ist.

f) $\frac{1}{2x}=0,5$

Versuche die Gleichung so umzustellen, dass du Brüche kürzen kannst.

$\begin{align} & & \frac{1}{2x} &=0,5 & & \mid \cdot 2x\\ \Leftrightarrow & & \frac{1}{2x} \cdot 2x &= 0,5 \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 1 &=0,5\cdot 2x & & \mid :0,5\\ \Leftrightarrow & & \frac{1}{0,5} &=\frac{0,5}{0,5} \cdot 2x & & \mid \text{kürzen}\\ \Leftrightarrow & & 2 &=2x & &\mid :2\\ \Leftrightarrow & & 1 &=x\\ & & \mathbb{L}=\{1\} \end{align}$

Probe:

$\begin{align} & & \frac{1}{2 \cdot 1} &=0,5 & &\\ \Leftrightarrow & & \frac{1}{2} &=0,5 & &\\ \Leftrightarrow & & 0,5 &=0,5 \end{align}$

g) $\frac{3}{z+1}=-\frac{5}{2z-1}$

Versuche die Variablen mit Hilfe der Multiplikation aus dem Nenner zu bekommen.

$\begin{align} & & \frac{3}{z+1} &= - \frac{5}{2z-1} & & \mid \cdot (z+1)\\ \Leftrightarrow & & \frac{3}{z+1} \cdot (z+1) &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 &= - \frac{5 \cdot (z+1)}{2z-1} & & \mid \cdot (2z-1)\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - \frac{5 \cdot (z+1)}{2z-1} \cdot (2z-1) & & \mid \text{kürzen}\\ \Leftrightarrow & & 3 \cdot (2z-1) &= - 5 \cdot (z+1) & &\\ \Leftrightarrow & & 6z-3 &= -5z-5 & & \mid +5z\\ \Leftrightarrow & & 11z-3 &= -5 & & \mid +3\\ \Leftrightarrow & & 11z &= -2 & & \mid :11\\ \Leftrightarrow & & z &= - \frac{2}{11}\\ & & \mathbb{L}=\{-\frac{2}{11}\} \end{align}$

Probe:

$\begin{align} & & \frac{3}{- \frac{2}{11} +1} &= - \frac{5}{2 \cdot (- \frac{2}{11}) -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{4}{11} -1} & &\\ \Leftrightarrow & & \frac{3}{\frac{9}{11}} &= - \frac{5}{- \frac{15}{11}} & & \mid \text{mit dem Kehrwert mal nehmen}\\ \Leftrightarrow & & 3 \cdot \frac{11}{9} &= - 5 \cdot - \frac{11}{15} & &\\ \Leftrightarrow & & \frac{33}{9} &= \frac{55}{15} & & \mid \text{kürzen}\\ \Leftrightarrow & & \frac{11}{3} &= \frac{11}{3} \end{align}$

Zahlenrätsel

Aufgabe 3: Finde die gesuchte Zahl

Wenn man zur Zahl $12$ das Doppelte einer Zahl addiert, so erhält man das Vierfache der gesuchten Zahl. Stelle eine geeignete Gleichung auf und gib die gesuchte Zahl an.

Überlege dir, wie man das Doppelte und das Vierfache einer Zahl als Term schreibt.

Zunächst übersetzen wir die Informationen aus der Aufgabenstellung in eine mathematische Schreibweise:

Das Doppelte einer Zahl: $2x$

Zur Zahl $12$ das Doppelte einer Zahl addieren: $2x+12$. Dies wird die linke Seite der Gleichung bilden.

Das Vierfache der gesuchten Zahl: $4x$. Dies ist die rechte Seite der Gleichung.

Wir erhalten also die Gleichung: $2x+12=4x$.

Um das gesuchte $x$ zu finden, lösen wir die Gleichung, indem wir sie nach $x$ umstellen. Achte darauf alle Umformungen immer auf beiden Seiten der Gleichung durchzuführen.

$\begin{align}& & 2x+12 & = 4x & &\mid -2x\\ \Leftrightarrow & & 12 & = 2x & &\mid :2\\ \Leftrightarrow & & 6 & = x \end{align}$

Die gesuchte Zahl ist $6$.

Probe:

$\begin{align} & & 2\cdot 6+12&=4\cdot 6 \\ \Leftrightarrow & &24&=24 \end{align}$

Aufgabe 4: Alter der Mutter

Die Mutter von Leon ist $3$-mal so alt wie er. In $12$ Jahren wird sie doppelt so alt sein wie Leon. Wie alt sind Leon und seine Mutter heute?

Beachte, dass sich das doppelte Alter auf das Alter in $12$ Jahren bezieht.

Bezeichne mit $M$ das Alter der Mutter und mit $L$ das Alter von Leon. Die erste Gleichung ist $\begin{align}M=3L\end{align}$,da die Mutter von Leon 3-mal so alt ist wie er. Außerdem gilt die zweite Gleichung $\begin{align}M+12=2(L+12)\end{align}$. Die linke Seite der Gleichung beschreibt das Alter der Mutter in 12 Jahren. Dies entspricht der rechten Seite der Gleichung, da das Alter der Mutter in 12 Jahren dann das doppelte des Alters von Leon in 12 Jahren beträgt.

Setze nun $\begin{align}M=3L \end{align}$ in die zweite Gleichung ein:

$\begin{align}\\ \Leftrightarrow & & 3L+12&=2L+24 & &\mid -12\\ \Leftrightarrow & & 3L&=2L+12 & &\mid -2L\\ \Leftrightarrow & & L=12 \end{align}$

Leon ist heute also 12 Jahre alt. Um das Alter der Mutter zu bestimmen, setzten wir $L=12$ in die erste Gleichung ein:

$\begin{align} & & M=3 \cdot 12 = 36 \end{align}$

Die Mutter ist heute also 36 Jahre alt.

Probe erste Gleichung:

$\begin{align}\\ & & 3\cdot 12=36 & &\\ \Leftrightarrow & & 36=36 & \end{align}$

Probe zweite Gleichung:

$\begin{align}\\ & & 36+12=2\cdot(12+12) & &\\ \Leftrightarrow & & 48=48 & \end{align}$

Leon ist heute $12$ Jahre alt und seine Mutter ist heute $36$ Jahre alt.

Rechnen mit Gleichungen im Sachzusammenhang

Aufgabe 5: Zwei-Felder-Ball-Feld abstecken

Nick und Tom sollen für ein Sportfest ein Zwei-Felder-Ball-Feld abstecken. Dafür sollen sie ein $66$ m langes Seil und sechs Pfosten verwenden. Für das Umwickeln aller Pfosten werden insgesamt drei Meter Seil benötigt. Das Spielfeld soll aus zwei gleichgroßen quadratischen Flächen bestehen. Wie lang ist eine Seite von einer der quadratischen Flächen, wenn man davon ausgeht, dass Nick und Tom das gesamte Seil benutzen?

Um die Gleichung aufzustellen, benötigst du den Umfang des Spielfeldes.

Benutze die Skizze, um einen Term für den Umfang des Spielfeldes aufzustellen.

Skizzierung des Spielfeldes

Beachte, dass zusätzlich Seil für das Abspannen an den Pfosten benötigt wird.

Die gesuchte Seitenlänge bezeichnen wir mit $x$.

Skizzierung des Spielfeldes

Den Umfang des Spielfeldes erhalten wir durch den Term $7x$.

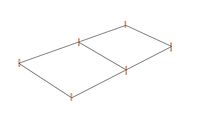
Wir erhalten die Gleichung: $7x+3=66$, da insgesamt $66$ Meter Seil zur Verfügung stehen und drei Meter Seil für die Abspannung an den Pfosten benötigt werden.

Diese Gleichung können wir lösen:

$\begin{align} & & 7x+3 &=66 & &\mid -3\\ \Leftrightarrow & & 7x &=63 & &\mid :7\\ \Leftrightarrow & & x &=9 \end{align}$

Probe:

$\begin{align} & & 7 \cdot 9 +3 &=66\\ \Leftrightarrow & & 63 + 3 &=66\\ \Leftrightarrow & & 66 &=66\\ \end{align}$

Eine Seite ist $9$ m lang.

Aufgabe 6: Getränkelager füllen

In einem Lager eines Restaurants sollen möglichst viele $35$ cm hohe Getränkekisten übereinander gestapelt werden. Die Raumhöhe beträgt $2,20$ m.

a) Wie viele Getränkekisten können übereinander gestapelt werden? Stelle eine Gleichung auf und berechne.

b) Eine Getränkekiste ist $40$ cm lang und $40$ cm breit. Das Lager hat eine Lagerfläche von $10$ m $\cdot$ $10$ m. Wie viele Getränkekisten finden insgesamt im Lager Platz?

Beachte die Umrechnung der Einheiten.

Berechne zuerst, wie viele Getränkekisten auf dem Boden der Lagerfläche Platz finden.

a) Zuerst wird die Höhe einer Getränkekiste in Meter umgerechnet: $35$ cm $=0,35$ m.

Jetzt kann die Gleichung aufgestellt werden: $0,35\cdot x=2,20$,

wobei $0,35$ die Höhe einer Getränkekiste in Metern und $2,20$ die Höhe des Lagerraumes in Metern angibt. Die Variable $x$ bezeichnet in der Gleichung die Anzahl der Kisten, die in den Lagerraum gestellt werden können.

Jetzt wird $x$ mit Hilfe der aufgestellten Gleichung berechnet:

$\begin{align} & & 0,35\cdot x &=2,20 & &\mid :0,35\\ \Leftrightarrow & & x &\approx 6,29 & &\\ \end{align}$

Probe:

$\begin{align} & & 0,35\cdot 6,29 \approx 2,20 & &\\ \Leftrightarrow & & 2,20 \approx 2,20 & &\\ \end{align}$

Das Ergebnis $6,29$ wird auf $6$ abgerundet, da nur ganze Kisten gestapelt werden können. Es können in dem Lagerraum also $6$ Getränkekisten übereinander gestapelt werden.

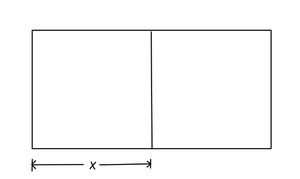
b) Zuerst legen wir den Boden der Lagerfläche mit Getränkekisten aus. Dazu stellen wir folgende Gleichung auf: $\begin{align} & & 10\cdot 10 &=0,4\cdot 0,4\cdot x & &\\ \Leftrightarrow & & 100 &=0,16\cdot x & &\mid :0,16\\ \Leftrightarrow & & 625 &=x \end{align}$

Probe:

$\begin{align} & & 10\cdot 10&=0,4\cdot 0,4\cdot 625 & &\\ \Leftrightarrow & & 100 &=0,16\cdot 625 & &\\ \Leftrightarrow & & 100 &=100 \end{align}$

In dieser Gleichung gibt der Teil $10\cdot 10$ die Grundfläche der Lagerfläche in m² an. Der Teil $0,4\cdot 0,4$ berechnet die Grundfläche der Getränkekisten in m². Die Variable $x$ bezeichnet die Anzahl der Getränkekisten.

Wir wissen nun also, dass $625$ Getränkekisten auf dem Boden der Lagerfläche Platz finden.

Aus Aufgabenteil a) wissen wir bereits, dass $6$ Getränkekisten übereinander gestapelt werden können. Also bleibt zu berechnen: $625\cdot 6=3750$.

Insgesamt finden demnach 3750 Getränkekisten auf der Lagerfläche Platz.