Digitale Werkzeuge in der Schule/Fit für VERA-8/Lineare Funktionen
In diesem Lernpfadkapitel hast du die Möglichkeit, dein Wissen über lineare Funktionen zu gebrauchen, zu erweitern und dein Verständnis zu vertiefen. Das Kapitel gibt dir eine Übersicht über die Zusammenhänge zwischen linearen Funktionen, die darauf liegenden Punkte und über die Gleichungen und Graphen linearer Funktionen.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
Inhaltsverzeichnis
Wiederholung: Was ist eine Funktion?
Zur Einführung in das Thema der linearen Funktionen wiederholen wir zunächst, was eine Funktion überhaupt ist. Versuche dazu, den folgenden Lückentext auszufüllen, indem du die Wörter unter dem Text mit der Maus an die passende Stelle im Text ziehst. Anschließend kannst du deine Antworten überprüfen.
Eine Zuordnung heißt Funktion, wenn jedem
-Wert genau ein
-Wert zugeordnet wird.
Funktionen werden häufig mit bezeichnet.
Durch eine Funktion wird einer Variablen
ein Funktionswert
zugeordnet.
Wenn es einen Term zur Berechnung der Funktionswerte gibt, dann nennt man ihn den Funktionsterm
und die zugehörige Gleichung heißt Funktionsgleichung.
Stellt man die Zahlenpaare als Punkte
in einem Koordinatensystem dar, so erhält man den Graphen der Funktion.
1.) Haus Adresse
(Ja, die Zuordnung beschreibt eine Funktion.)
(!Nein, die Zuordnung beschreibt keine Funktion.)
2.) Mutter Kind
(!Ja, die Zuordnung beschreibt eine Funktion.)
(Nein, die Zuordnung beschreibt keine Funktion.)
3.) Zahl Quersumme der Zahl
(Ja, die Zuordnung beschreibt eine Funktion.)
(!Nein, die Zuordnung beschreibt keine Funktion.)
Lineare Funktionen erkennen
Lineare Funktionen sind dir vielleicht auch unter der Bezeichnung Geradengleichung bekannt. Wie dieser Name schon sagt, handelt es sich bei dem Graphen einer linearen Funktion um eine Gerade. Der Graph kann daher keine Kurven haben.
Im Allgemeinen haben lineare Funktionen die Funktionsgleichung .
- Dabei ist
die Steigung der Geraden und
der
-Achsenabschnitt, also der Schnittpunkt mit der
-Achse.
- Das Vorzeichen der Steigung
gibt an, ob die Gerade fällt (negatives Vorzeichen) oder steigt (positives Vorzeichen).
- Den Schnittpunkt mit der
-Achse, die sogenannte Nullstelle der Funktion, berechnest du, indem du
setzt. Denn an dem Punkt, wo der Graph die
-Achse schneidet, ist der
-Wert gleich
.
Im Folgenden kannst du über die beiden Schieberegler die Steigung und den
-Achsenabschnitt
verstellen und dir anschauen, wie sich der Graph der linearen Funktion verändert. Mit deiner Maus kannst du die Grafik verschieben oder rein- und herauszoomen.

Entscheide, ob die folgenden Funktionsgleichungen und Graphen lineare Funktionen sind, und ordne sie dem passenden Feld zu.
Wenn du alle Funktionsgleichungen und Graphen zugeordnet hast, kannst du dein Ergebnis mit einem Klick auf den blauen Haken unten rechts überprüfen.
Funktionsgraph erkennen: Überlege dir, welche geometrische Form der Graph einer linearen Funktionen hat.
Funktionsgleichung erkennen: Überlege dir, welche Form die allgemeine Funktionsgleichung einer linearen Funktion hat.
Graph einer linearen Funktion
a)
b)
c)
Es gibt zwei mögliche Wege einen Graphen zu zeichnen.
Entweder du betrachtest und
von der Funktionsgleichung
genauer. Dieses Verfahren wird dir bei der Möglichkeit 1 genauer erläutert.
Oder du setzt Punkte in die Funktionsgleichung ein. Die Möglichkeit 2 zeigt dir hierzu ein Beispiel.
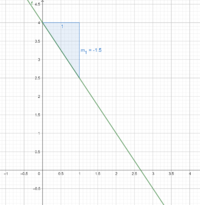
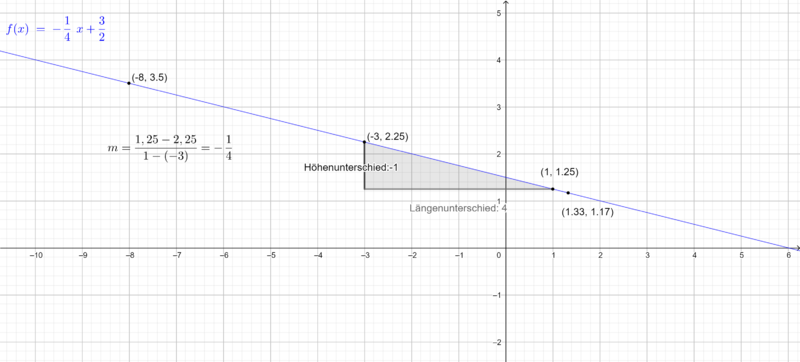
Betrachten wir als Beispiel die Funktionsgleichung .
Dabei gibt den Schnittpunkt mit der y- Achse im Koordinatensystem an. Wir wissen also, dass der Graph der Funktion durch den Punkt
verläuft.
Nun betrachten wir die Steigung welche durch gegeben ist. Du kannst dann vom Punkt
eine Einheit nach rechts und 1,5 nach unten gehen, weil die Steigung negativ ist.
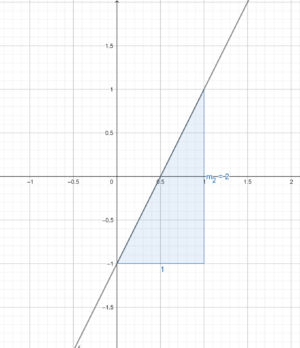
Betrachten wir erneut die Funktionsgleichung
Bei diesem Verfahren setzt du zwei verschiedene x-Werte in die Gleichung ein. Versuche einfache Werte zu wählen.
Du könntest zum Beispiel wählen. Dann wäre
Dies wäre der Punkt
.
Als nächstes wählst du eine andere Zahl, z.B. . Dann wäre
. Dies wäre der Punkt
.
Möglichkeit 1:
Die Funktionsgleichung schneidet die y- Achse im Punkt
,da
den Schnittpunkt mit der y-Achse angibt. Diesen Wert kannst du also direkt ablesen.
Nun betrachten wir die Steigung . Wir können vom Punkt
nun eine Einheit nach rechts und 2 nach oben gehen, da die Steigung positiv ist.
Verbindet man nun diese Punkte, so erhält man den Graph der Funktion.
Möglichkeit 2:
Bei dieser Lösungsmöglichkeit wählen wir zwei verschiedene x- Werte.
Zunächst könnte man in die Funktionsgleichung einsetzten und man erhält
, also den Punkt
.
Als nächstes könnte man z.B. wählen. Dann erhält man durch einsetzten in die Funktionsgleichung
. Dies wäre dann der Punkt
.
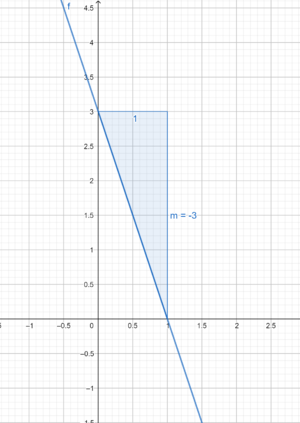
Möglichkeit 1:
Die Funktionsgleichung schneidet die y- Achse im Punkt
,da
den Schnittpunkt mit der y-Achse angibt. Diesen Wert kannst du also direkt ablesen.
Nun betrachten wir die Steigung . Wir können vom Punkt
nun eine Einheit nach rechts und 3 nach unten gehen, da die Steigung negativ ist.
Verbindet man nun diese Punkte, so erhält man den Graph der Funktion.
Möglichkeit 2:
Bei dieser Lösungsmöglichkeit wählen wir zwei verschiedene x- Werte.
Zunächst könnte man in die Funktionsgleichung einsetzten und man erhält
, also den Punkt
.
Als nächstes könnte man z.B. wählen. Dann erhält man durch einsetzten in die Funktionsgleichung
. Dies wäre dann der Punkt
.
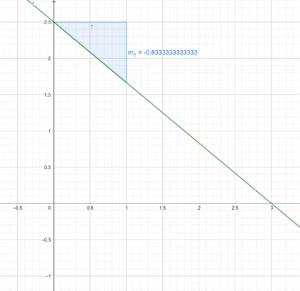
Möglichkeit 1:
Die Funktionsgleichung schneidet die y- Achse im Punkt
,da
den Schnittpunkt mit der y-Achse angibt. Diesen Wert kannst du also direkt ablesen.
Nun betrachten wir die Steigung . Wir könnten vom Punkt
nun eine Einheit nach rechts und
nach unten gehen, da die Steigung negativ ist.
Da dies allerdings schwierig und ungenau abzulesen ist, bietet es sich hier an stattdessen ein Vielfaches der Steigung zu gehen. Multiplizieren wir die Steigung z.B. mit 3 erhalten wir . Dieser Wert ist deutlich einfacher einzuzeichnen in ein Koordinatensystem. Wir gehen nun also von dem Punkt
3 Einheiten nach rechts, weil wir die Steigung ja mit 3 multipliziert haben. Dann gehen wir 2,5 Einheiten nach unten, da die Steigung negativ ist. Nun sind wir bei dem Punkt
ausgekommen, welchen man gut in ein Koordinatensystem einzeichnen kann.
Verbindet man nun diese Punkte, so erhält man den Graph der Funktion.
Möglichkeit 2:
Bei dieser Lösungsmöglichkeit wählen wir zwei verschiedene x- Werte.
Zunächst könnte man in die Funktionsgleichung einsetzten und man erhält
, also den Punkt
.
Als nächstes könnte man z.B. wählen. Dann erhält man durch einsetzten in die Funktionsgleichung
. Dies wäre dann der Punkt
.
Verbinde den Graphen mit der passenden Funktionsgleichung.
Bestimmung von Funktionsgleichungen
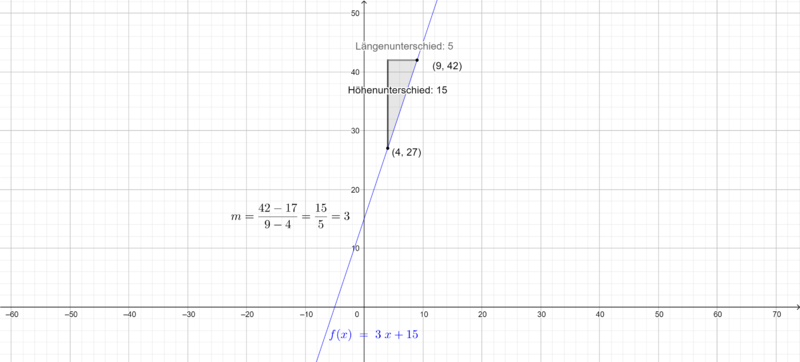
Die Steigung einer linearen Funktion erhältst du mithilfe des Steigungsdreiecks, von welchem zwei Punkte auf dem Graphen liegen. Das Steigungsdreieck kennzeichnet, dass die Steigung dem Verhältnis des Höhen- und Längenunterschiedes beider Punkte entspricht.
Die Steigung berechnest du folgendermaßen:
- Du suchst zwei beliebige Punkte
und
, die auf dem Graphen der Funktion liegen.
- Um den Höhenunterschied der Punkte zu bestimmen, benötigt man die y- bzw. f(x)-Koordinaten der Punkte P und Q: Höhenunterschied:
- Um den Längenunterschied der Punkte zu bestimmen, benötigt man die x-Koordinaten der Punkte P und Q: Längenunterschied:
- Für die Steigung der Geraden gilt dann:

Nutze die in den folgenden Teilaufgaben genannten Punkte, durch welche eine Gerade verläuft. Bestimme in deinem Heft die jeweilige Gleichung der Geraden in der Form .
Du kannst auf drei unterschiedlichen Wegen die Funktionsgleichungen bestimmen.
- Berechne zuerst die Steigung
. Gehe dabei wie im Merkkasten zum Steigungsdreieck vor.
- Berechne dann den y-Achsenabschnitt
. Setze die Steigung und einen der beiden Punkte in die Geradengleichung
ein.
- Du stellst zwei Gleichungen mit jeweils den Unbekannten
und
auf. Dabei setzt du die x-Koordinaten der Punkte
und
für
und die
bzw.
-Koordinaten der Punkte
und
für
in die Geradengleichung
ein.
- Beide Gleichungen ergeben zusammen ein lineares Gleichungssystem, welches du mit verschiedenen Verfahren, wie das Gleichsetzungsverfahren, lösen kannst, um die beiden Unbekannten
und
zu bestimmen.
- Die beiden Unbekannten
und
setzt du schließlich in die Geradengleichung
ein.
- Zeichne die Punkte
und
in ein Koordinatensystem.
- Zeichne dann eine Gerade, die durch die Punkte
und
verläuft.
- Bestimme anschließend mit Hilfe des Steigungsdreiecks, welches oben im Merkkästchen nochmal erklärt worden ist, die Steigung
.
- Lies den y-Achsenabschnitt
am Graphen ab.
- Setze die Werte für m und b in die Geradengleichung
ein.
a) Gegeben sind die Punkte und
.
Die Funktionsgleichung lautet
- Für den Höhenunterschied der Punkte musst du die y- bzw. f(x)-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
verwenden. Dann rechnen wir wie folgt:
- Für die Steigung
der Geraden setzt du beide Werte in die folgende Gleichung ein:
- Für die Berechnung des y-Achsenabschnitts setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein.
- Wenn du als Punkt
gewählt hast, erhältst du
- Wenn du als Punkt
gewählt hast, erhältst du
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Forme dann beide Gleichungen nach b um und setze sie
.
- Dann löst du eine Gleichung nach
auf und erhältst
.
- Die Steigung setzt du anschließend in die andere Gleichung für
ein und erhältst
.
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
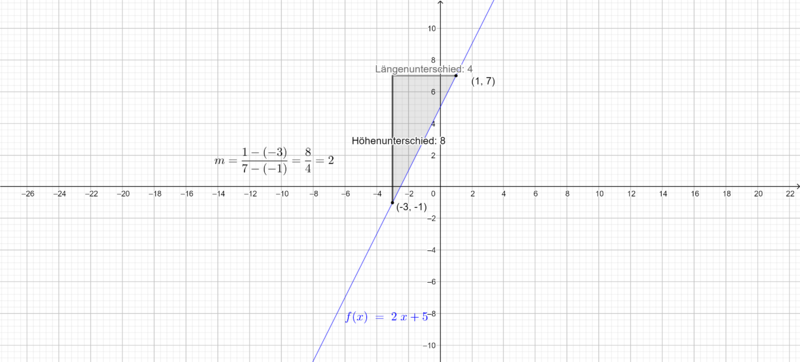
b) Gegeben sind die Punkte und
.
Die Funktionsgleichung lautet .
- Für den Höhenunterschied der Punkte musst du die y bzw. f(x)-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
verwenden. Dann rechnen wir wie folgt:
- Für die Steigung
der Geraden setzt du beide Werte in die folgende Gleichung ein:
- Für die Berechnung des y-Achsenabschnitts setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein.
- Wenn du als Punkt
gewählt hast, erhältst du
- Wenn du als Punkt
gewählt hast, erhältst du
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Forme dann beide Gleichungen nach b um und setze sie
.
- Dann löst du eine Gleichung nach
auf und erhältst
.
- Die Steigung setzt du anschließend in die andere Gleichung für
ein und erhältst
.
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
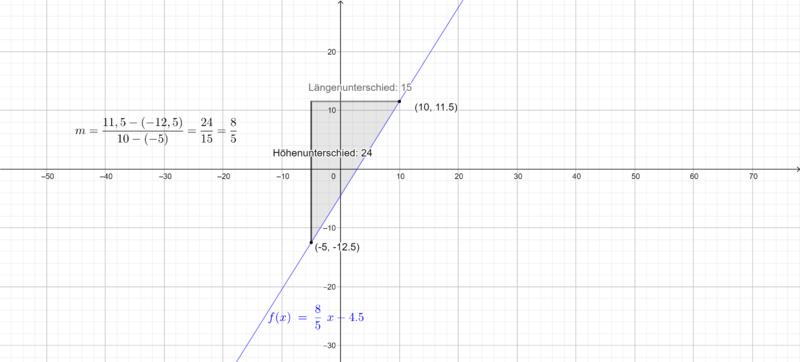
c) Gegeben sind die Punkte und
.
Die Funktionsgleichung lautet .
- Für den Höhenunterschied der Punkte musst du die y bzw. f(x)-Koordinaten der Punkte
und
wie folgt berechnen:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der Punkte
und
verwenden. Dann rechnen wir wie folgt:
- Für die Steigung
der Geraden setzt du beide Werte in die folgende Gleichung ein:
- Für die Berechnung des y-Achsenabschnitts setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein.
- Wenn du als Punkt
gewählt hast, erhältst du
- Wenn du als Punkt
gewählt hast, erhältst du
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Forme dann beide Gleichungen nach b um und setze sie
.
- Dann löst du eine Gleichung nach
auf und erhältst
.
- Die Steigung setzt du anschließend in die andere Gleichung für
ein und erhältst
.
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
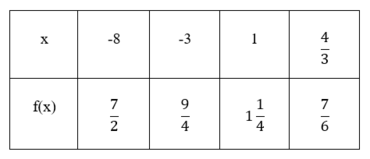
Die Funktionsgleichung lautet .
- Für den Höhenunterschied der Punkte musst du die y bzw. f(x)-Koordinaten zweier Punkte der Wertetabelle berechnen. Wir wählen zum Beispiel die Punkte
und
und berechnen wie folgt:
- Für den Längenunterschied der Punkte musst du die x-Koordinaten der gleichen Punkte, die du beim Höhenunterschied gewählt hast, verwenden. Wir benutzen also die Punkte
und
. Dann rechnen wir wie folgt:
- Für die Steigung
der Geraden setzt du beide Werte in die folgende Gleichung ein:
- Für die Berechnung des y-Achsenabschnitts setzt du die Steigung
und einen der Punkte in die Geradengleichung
ein.
- Wenn du als Punkt
gewählt hast, erhältst du
- Wenn du als Punkt
gewählt hast, erhältst du
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
- Die beiden Gleichungen, die sich durch das Einsetzen der Punkte
und
in die Geradengleichung
ergeben, sind
und
.
- Forme dann beide Gleichungen nach b um und setze sie
.
- Dann löst du eine Gleichung nach
auf und erhältst
.
- Die Steigung setzt du anschließend in die andere Gleichung für
ein und erhältst
.
- Zum Schluss setzt du
und
in die Geradengleichung
ein.
In den folgenden Teilaufgaben ist dir jeweils die Steigung der Geraden und ein Punkt, der auf der Geraden liegt, gegeben. Bestimme die jeweilige Gleichung der Geraden in der Form in deinem Heft.
a) Die Steigung ist und der Punkt
.
- Setze als erstes für die Steigung
ein, sodass die Gleichung
entsteht.
- Nutze die Angabe des Punktes
. Dann erhälst du mit
und
die Gleichung
erhältst.
- Bestimme mit Auflösung nach
den Wert
. Schließlich erhälst du, wenn du die Werte für m und b einsetzt, die Geradengleichung
ergibt.
b) Die Steigung ist und der Punkt
.
- Setze als erstes für die Steigung
ein, sodass die Gleichung
entsteht.
- Nutze die Angabe des Punktes
. Dann erhälst du mit
und
die Gleichung
erhältst.
- Bestimme mit Auflösung nach
den Wert
. Schließlich erhälst du, wenn du die Werte für m und b einsetzt, die Geradengleichung
ergibt.
c) Die Steigung ist und der Punkt
- Setze als erstes für die Steigung
ein, sodass die Gleichung
entsteht.
- Nutze die Angabe des Punktes
. Dann erhälst du mit
und
die Gleichung
erhältst.
- Bestimme mit Auflösung nach
den Wert
. Schließlich erhälst du, wenn du die Werte für m und b einsetzt, die Geradengleichung
ergibt.
Graphen und ihre Punkte
Prüfe, ob die Punkte auf dem jeweiligen Graphen liegen.
In der Aufgabe siehst du in der obersten Zeile vier verschiedene Funktionsgleichungen. Zu Beginn ist die erste Funktionsgleichung blau hinterlegt. Hiermit kannst du starten. Wähle die zu dieser Gleichung gehörigen Punkte aus. Hast du alle passenden Punkte ausgewählt, klicke oben die nächste Funktionsgleichung an und wiederhole dein Vorgehen.
Viel Spaß!
Schnittpunkte von linearen Funktionen
Linearen Funktionen haben immer einen Schnittpunkt mit der -Achse, den
-Achsenabschnitt. Zusätzlich schneiden alle Funktionen, die nicht konstant sind, die
-Achse. Diesen Punkt nennt man auch die Nullstelle der Funktion, da der zugehörige
-Wert an dieser Stelle immer gleich
ist. Aber es können sich auch zwei lineare Funktionen in einem Punkt schneiden.
Du kannst den Schnittpunkt von linearen Funktionen auf zwei Arten bestimmen.
- Rechnerisch
- Graphisch
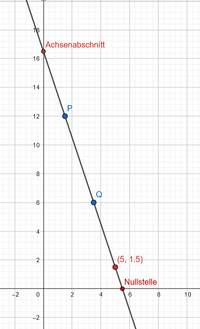
Schnittpunkt mit der x-Achse (Nullstelle)
Die Nullstelle einer linearen Funktion ist der Schnittpunkt der Funktion mit der -Achse. Die Berechnung ist daher oftmals leichter als die Berechnung des Schnittpunktes zweier linearer Funktionen, da der
-Wert bereits bekannt ist, dieser ist immer
.
Bestimme graphisch und rechnerisch im Heft die Nullstellen der folgenden Funktionen.
a)
b)
c)
d)
Gehe folgendermaßen vor:
Schritt 1: Setze die Gleichung gleich .
Schritt 2: Löse nach auf.
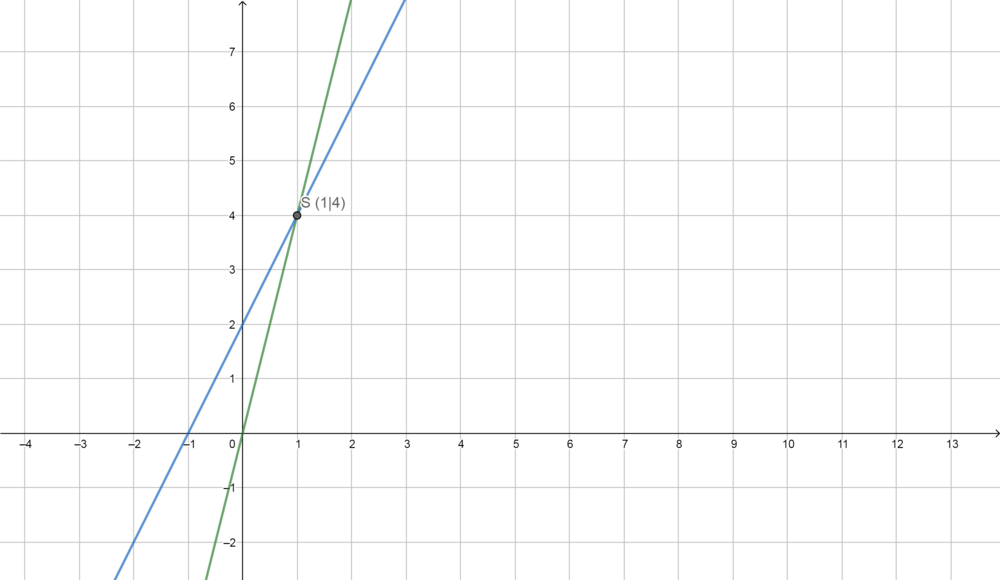
Schnittpunkt von zwei linearen Funktionen
Beantworte die folgenden Fragen zu Schnittpunkten von linearen Funktionen.
Bestimme den Schnittpunkt von und
. Überlege dir, ob du den Schnittpunkt graphisch oder rechnerisch lösen möchtest.
Schritt 1: Zeichne die Funktionen in ein Koordinatensystem ein.
Schritt 2: Markiere den Schnittpunkt durch ein Kreuz und lies die Koordinaten ab. Beschrifte den Schnittpunkt.
Gehe folgendermaßen vor:
Schritt 1: Setze beide Funktionsgleichungen gleich.
Schritt 2: Löse die Gleichung nach x auf.
Schritt 3: Bestimme . Setze dazu
in eine der beiden Funktionsgleichungen ein.
Schritt 4: Probe. Setze auch in die andere Funktionsgleichung ein.
Schritt 5: Gib den Schnittpunkt an.
Anwendungsaufgaben / Modellierungsaufgaben
Löse die folgenden Aufgaben in deinem Heft.
a) Zeichne den Graphen der Zuordnung Zeit Länge der Kerze.
b) Lies an deiner Zeichnung folgende Werte ab:
- Wie lang war die Kerze zu Beginn?
- Nach welcher Brennzeit ist sie nur noch 1,5 cm hoch?
- Wann ist sie abgebrannt?
c) Bestimme die Änderungsrate und gib die Funktionsgleichung in der Form an.
Ermittle nun die gesuchten Werte aus b) mithilfe der Gleichung.
Den
- 'Zu Beginn' bedeutet, dass
ist. Also musst du den
-Achsenabschnitt ablesen. Dieser ist
. Zu Beginn war die Kerze also 16,5cm hoch.
- Die Brennzeit, bei der die Kerze noch 1,5cm hoch ist, beträgt 5 Stunden. Dies erhältst du, indem du den
-Wert zum Wert
abließt. Dieser ist
.
- 'Abgebrannt' bedeutet, dass die Höhe gleich
ist, also
. Du sollst also die Nullstelle ablesen. Diese ist
. Also ist die Kerze nach 5,5 Stunden abgebrannt.
Die Änderungsrate ist die Steigung der Geraden. Diese berechnest du mit den oben ermittelten Punkten
und
wie folgt:
.
Den -Achsenabschnitt hast du schon bei Teilaufgabe b) ermittelt. Dieser war
.
Setze und
nun in die allgemeine Form
ein. Du erhältst dann:
.
- 'Zu Beginn' bedeutet, dass
ist. Also
.
- Du weißt, dass die Höhe noch 1,5cm beträgt. Setze also
. Dann gilt:
.
- 'Abgebrannt' bedeutet, dass die Höhe gleich
ist. Setze also
. Dann gilt:
.
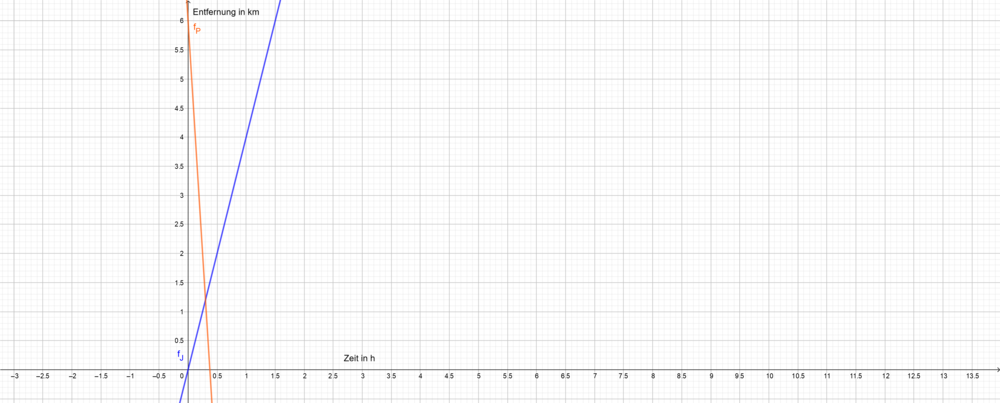
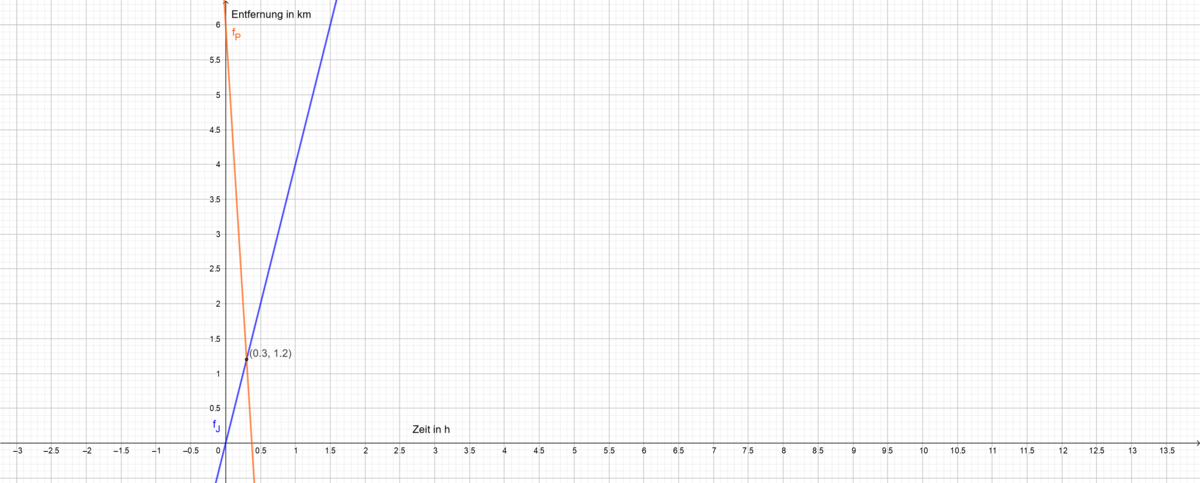
Johannes geht zu Fuß von zu Hause aus zur 6 km entfernten Sporthalle zum Fußballtraining. Er geht relativ konstant mit 4 km/h. Pauk steht schon vor der Sporthalle. Er startet zur gleichen Zeit wie Johannes mit seinem Fahrrad und fährt ihm entgegen. Paul fährt mit einer konstanten Geschwindigkeit von 16 km/h. Beide nehmen den selben Weg. Wann und wo treffen sie sich?
Überlege, welche der oben genannten Werte die Steigung und welche den y-Achsenabschnitt der verschiedenen Funktionen darstellt. Male es dir graphisch in einem Koordinatensystem auf und überlege, welche Einheit auf der x- und welche auf der y-Achse steht. Stelle dann die entsprechenden Funktionsgleichungen auf.
Durch die oben genannten Daten stellst du die Funktionsgleichungen auf. Johannes' Geschwindigkeit 4km/h stellt die Steigung m der Gleichung dar. Johannes ist auf dem Weg zur Trainigshalle, also ist sein Startpunkt bei 0km. Somit erhält man für Johannes die Gleichung , wobei x die Zeit in Stunden verkörpert. Paul fährt ihm mit 16 km/h entgegen. Da er in entgegengesetzter Richtung zu Johannes fährt, ist die Steigung der Gleichung negativ. Du bekommst die Gleichung
. Da Paul an der Sporthalle startet, ist der Wert b=6 für den y-Achsenabschnitt. Somit erhält man die Gleichung
.
Jetzt hast du zwei Möglichkeiten:
- Du setzt die Funktionsgleichungen
gleich:
. Nach Umformungen erhälst du die Gleichung
. Mit Auflösen nach x ergibt sich die Gleichung
. Dieser x-Wert wird in eine der zwei Gleichungen eingesetzt. Setze x=0,3 in
ein und berechne das Produkt. Das ergibt
.
- Du zeichnest beide Graphen und liest den Schnittpunkt der Geraden ab.
Maria möchte im Internet surfen und begutachtet die Tarife A, B und C.
Tarif A: Grundgebühr 5 € / Monat die ersten 5 Stunden frei, dann 1 Ct./min.
Tarif B: Grundgebühr 10 € / Monat die ersten 10 Stunden frei, dann 0,8 Ct./min.
Tarif C: Flat–Rate 40 € / Monat.
Maria surft im Durchschnitt zwei Stunden am Tag (30 Tage / Monat).
a) Stelle für jeden Tarif die Funktionsgleichung auf.
b) Zeichne die Funktionsgraphen in ein geeignetes Koordinatensystem.
c) Erkläre, was du am Graphen ablesen kannst.
d) Berechne den günstigsten Tarif für Maria.
e) In welchem Punkt herrscht Kostengleichheit für Tarif A und B?
f) Ab welcher Surfzeit ist Tarif C der günstigste?
Versuche zunächst die Einheiten zu normen, also entscheide dich entweder für min oder h, bzw. ct oder € .
Es ist üblich eher in €/h zu rechnen. Den ct/min Wert könntest du dann mit 60 min multiplizieren um auf ct/h zu kommen.
Wie könnte dieser Wert dann in €/h umgewandelt werden?
Nun kannst du eine vorübergehende Funktionsgleichung mit f(x)= dem Wert €/h x+ a (einen noch unbekannten Wert) aufstellen.
Dann überlege dir, was die Freistunden bedeuten?!
Welchen Punkt erhalten wir dadurch?
Versuche dies in die Funktionsgleichung mit einzubauen indem du den Punkt einsetzt und die Gleichung auflöst.
Um die Funktionsgleichung in ein Koordinatensystem zu übertragen, überlege dir zunächst welche Werte deine x- Achse und, welche Werte deine y-Achse angibst.
Probiere einen geeigneten Maßstab zu wählen indem du vorher einige Werte (auch höhere) in die Funktionsgleichung eingibst.
Falls du mit dem Zeichnen von Graphen Schwierigkeiten hast, wiederhole das entsprechende Kapitel in diesem Lernpfad. Da werden dir zwei Möglichkeiten einen Graphen zu zeichnen vorgestellt.
Falls du die Graphen alle in ein Koordinatensystem gezeichnet hast, kannst du einiges an diesen ablesen.
Zum Beispiel welcher Tarif wann am billigsten ist oder wann die Tarife gleich sind. Schaue dir dazu die Schnittpunkte genauer an und probiere diese zu interpretieren.Um den günstigen Tarif für Maria zu berechnen, müssen wir zunächst aus der Aufgabe herauslesen wie lange Maria im Monat surft.
Sie surft 2h am Tag. Diesen Wert muss man jetzt noch auf den Monat umrechnen. Wie viele Stunden surft Maria in 30 Tagen(einem Monat)?
Tarif A:
Zunächst multipliziert man die 1ct/min mit 60 min, um diesen Wert in ct/h zu haben. min
ct/min
ct/h
Nun wandelst du diesen Wert in €/h um. ct/h
€/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung.
, wobei a ein noch unbekannter Wert ist.
Wir wissen, dass die ersten 5 Stunden frei sind,d.h hier muss nur die Grundgebühr von 5€ bezahlt werden. Der Punkt muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von
einsetzten und nach a auflösen, um die ganze Funktionsgleichung zu erhalten.
.
Die Funktionsgleichung für Tarif A ist also . Beachtet jedoch, dass die Funktion bis
konstant 5 ist.
Tarif B:
Zunächst multipliziert man die 0,8ct/min mit 60 min, um diesen Wert in ct/h zu haben. min
ct/min
ct/h
Nun wandelst du diesen Wert in €/h um. ct/h
€/h. Wir kennen jetzt schon einen Teil der Funktionsgleichung.
, wobei a ein noch unbekannter Wert ist.
Wir wissen, dass die ersten 10 Stunden frei sind,d.h hier muss nur die Grundgebühr von 10€ bezahlt werden. Der Punkt muss also auf dem Graphen unserer Funktionsgleichung liegen. D.h. wir können diesen Punkt nun in die Funktionsgleichung von
einsetzten und nach b auflösen, um die ganze Funktionsgleichung zu erhalten.
.
Die Funktionsgleichung für Tarif B ist also . Beachtet jedoch, dass die Funktion bis
konstant 10 ist.
Tarif C:
Da dies eine Flatrate ist, wird ein Wert für jeden Monat festgesetzt und dieser Wert verändert sich auch nicht wenn mehr oder weniger Stunden gesurft wird. Deshalb ist die Funktion eine Konstante.
In dieser Grafik entspricht ,
und

Der Schnittpunkt sagt aus, dass der Tarif A selbst wenn man gar keine Zeit im Internet surft man dennoch 5 € bezahlen muss.
Der Punkt ist uns bereits aus dem Teil a bekannt. Bis zu diesem Punkt läuft der Graph konstant, da die ersten 5 Stunden frei sind, danach verläuft die Funktion linear.
Der Punkt ist beim Tarif B der Schnittpunkt mit der y-Achse. Auch hier gilt also, dass selbst wenn Maria gar nicht im Internet surft sie dennoch 10 € bezahlen muss.
Den Punkt kennen wir schon aus dem Teil a dieser Aufgabe. Bis zu diesem Punkt läuft die Funktion des Tarifs B konstant, da die ersten 10 Stunden frei sind.
Der Punkt ist der Schnittpunkt der beiden Funktion f(x) und g(x). Das heißt an diesem Punkt sind die Tarife für Maria gleich teuer.
Der Punkt ist der Schnittpunkt der Funktionen f(x) und h(x). An diesem Punkt sind die beiden Tarife A und C also gleich teuer für Maria.
Der Punkt ist der Schnittpunkt der Funktionen g(x) und h(x). Die beiden Tarife sind in diesem Punkt gleich teuer.

Zunächst bestimmen wir die Stundenzahl, welche Maria pro Monat fürs surfen nutzt. Maria surft 2h/Tag. Da ein Monat 30 Tage hat, kann man, kann man 30 und 2 multiplizieren und erhält 60 h/Monat.
Nun setzten wir die 60 h als x- Wert in die Funktionsgleichungen von f(x),g(x) und h(x) ein und vergleichen das Ergebnis.
Hier ist nach dem Schnittpunkt von f(x) und g(x) gefragt. Dazu setzt man die Gleichungen gleich und löst sie nach x auf.
Um dies herauszufinden brauchen wir die Schnittpunkte der Funktionsgleichungen f(x),g(x) mit h(x), da f und g danach größer als h sind und somit h (also der Tarif C) dann der günstigste wäre.