Digitale Werkzeuge in der Schule/Fit für VERA-8/Einfache Gleichungen

Info

In diesem Lernpfadkapitel kannst du das Wichtigste zum Thema Einfache Gleichungen lernen. Kurzbeschreibung des Aufbaus. Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit grünem Streifen sind Aufgaben hoher Schwierigkeit.

Viel Erfolg!

Hier sollen noch die Ziele bzw. der Aufbau des Kapitels und ggf. Hinweise für Lehrkräfte ergänzt werden.

Die wichtigsten Definitionen und Begriffe in diesem Kapitel

Die wichtigsten Begriffe, die du zum Bearbeiten der Aufgaben benötigst, werden hier in Merkkästen erklärt. Sollten dir diese Begriffe schon vertraut sein, kannst du diesen Teil überspringen und mit den Aufgaben starten. Falls du während der Bearbeitung einer Aufgabe unsicher bist, kannst du immer in diesen Abschnitt zurückkehren und dir die Merkkästen erneut durchlesen.

Variable

Variablen sind sogenannte "Platzhalter" in Gleichungen. Man kann für diesen "Platzhalter" jederzeit Zahlen einsetzen, sodass die Gleichung korrekt bleibt. Es wird aber nicht festgelegt für welche Zahl, weshalb diese "variabel" bleibt. Die "Platzhalter" sind in den meisten Fällen Buchstaben, beispielsweise ein "x".

Term

Ein Term ist eine Kombination aus Variablen, Zahlen, mathematischen Verknüpfungen ($+$,$-$,...) und Klammern.

Beispiele sind:

$x+y$ oder

$d\cdot (3+5x)$ oder

$3+4-2$.

Gleichung

Eine Gleichung ist ein mathematischer Ausdruck, der aus zwei Termen besteht, die durch ein „$=$“–Zeichen miteinander verbunden sind.

Lösungsmenge

Um eine Gleichung zu lösen, müssen alle Zahlen gefunden werden, für die beim Einsetzen die Gleichung erfüllt ist. Die Menge aller Lösungen wird Lösungsmenge $\mathbb{L}$ genannt.

Beispiel:

Die Gleichung $5-x=3$ lässt sich leicht lösen: $x=2$. Dann erhalten wir die Löungsmenge $\mathbb{L}=\{2\}$.

Alles in der Waage

Aufgabe 1: Titel

Bring die Waage für verschiedene $x$ ins Gleichgewicht. Nimm dann auf beiden Seiten der Waage gleich viele Kugeln weg. Was kannst du beobachten?

Gleichungen lösen

Beispiel 1: Richtig Gleichungen lösen

Wenn du eine Gleichung lösen möchtest, musst du sie zunächst nach der Variable auflösen. Diese Variable soll am Ende isoliert, d.h. alleine, auf einer Seite der Gleichung stehen. Wir schauen uns ein Beispiel an:

$(x+5)^{2}=x^{2}+35$

Um diese Gleichung zu lösen, müssen wir zunächst die binomische Formel berechnen.

$\begin{align} && (x+5)^{2}&=x^{2}+35\\ \Leftrightarrow & & x^{2}+10x+25&=x^{2}+35\\ \end{align}$.

Jetzt können wir wie gewohnt nach $x$ auflösen.

$\begin{align} & & (x+5)^{2}&=x^{2}+35\\ \Leftrightarrow & & x^{2}+10x+25&=x^{2}+35 & &\mid -x^{2}\\ \Leftrightarrow & & 10x+25&=35 & &\mid -25\\ \Leftrightarrow & & 10x&=10 & &\mid :10\\ \Leftrightarrow & & x&=1 \end{align}$

Probe:

$\begin{align} & &(1+5)^{2}&=1^{2}+35\\ \Leftrightarrow & & 36&=36 \end{align}$.

Wir erhalten also die Lösungsmenge $\mathbb{L}=\{1\}$.

Aufgabe 2: Lösungsmenge bestimmen

Bestimme die Lösungsmenge der Gleichung. Führe, wenn möglich, eine Probe durch.

Wenn du nicht mehr weißt, was die Lösungsmenge ist, schau bei den Definitionen nach.

a) $x^{2}-64=0$

$\begin{align} & & x^{2}-64 &=0 & &\mid +64\\ \Leftrightarrow & & x^{2} &=64 & &\mid \pm \sqrt{}\\ \Leftrightarrow & & x =-8 &\lor x=8\\ & & \mathbb{L}=\{-8,8\} \end{align}$

Probe:

$\begin{align} & & (-8)^{2}-64 &=0 \\ \Leftrightarrow & & 64-64 &=0\\ \Leftrightarrow & & 0 &=0 \end{align}$

$\begin{align} & & 8^{2}-64 &=0 \\ \Leftrightarrow & & 64-64 &=0\\ \Leftrightarrow & & 0 &=0 \end{align}$

b) $4(x+1)-4x-5=1$

$\begin{align} & & 4(x+1)-4x-5 &=1\\ \Leftrightarrow & & 4x+4-4x-5 &=1\\ \Leftrightarrow & & 4x-4x+4-5 &=1\\ \Leftrightarrow & & -1 &=1 \end{align}$

Das ist ein Widerspruch. Deshalb ist die Lösungsmenge leer: $\mathbb{L}=\{\}$.

c) $x\cdot (x-5)=0$

Ein Produkt ist dann $0$, wenn einer der Faktoren $0$ ist. Deshalb kann man die Aufgabe so lösen:

$\begin{align} & & x\cdot (x-5)&=0\\ \Leftrightarrow & & x=0 &\or x-5=0\\ \Leftrightarrow & & x=0 &\or x=5\\ & & \mathbb{L}\{0,5\} \end{align}$

Probe:

$\begin{align} & & 0\cdot (0-5)&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

$\begin{align} & & 5\cdot (5-5)&=0\\ \Leftrightarrow & & 5\cdot 0&=0\\ \Leftrightarrow & & 0&=0 \end{align}$

d) $3x+7=16$

$\begin{align} & & 3x+7&=16 & &\mid -7\\ \Leftrightarrow & & 3x &=9 & &\mid :3\\ \Leftrightarrow & & x &=3\\ & & \mathbb{L}=\{3\} \end{align}$

Probe:

$\begin{align} & & 3\cdot 3+7&=16\\ \Leftrightarrow & & 9+7 &=16\\ \Leftrightarrow & & 16 &=16 \end{align}$

e) $(x+3)^{2}-x^{2}=25$

$\begin{align} & & (x+3)^{2}-x^{2}&=25 & & \\ \Leftrightarrow & & x^{2}+6x+9-x^{2}&=25 & &\\ \Leftrightarrow & & 6x+9 &=25 & &\mid -9\\ \Leftrightarrow & & 6x &=16 & &\mid :6\\ \Leftrightarrow & & x &=\frac{16}{6}\\ \Leftrightarrow & & x &=\frac{8}{3}\\ & & \mathbb{L}=\{\frac{8}{3}\} \end{align}$

Probe:

$\begin{align} & & \left(\frac{8}{3}+3\right)^{2}-\left(\frac{8}{3}\right)^{2}&=25\\ \Leftrightarrow & & \left(\frac{17}{3}\right)^{2}-\left(\frac{8}{3}\right)^{2}&=25\\ \Leftrightarrow & & \frac{289}{9}-\frac{64}{9} &=25\\ \Leftrightarrow & & \frac{289-64}{9} &=25\\ \Leftrightarrow & & \frac{225}{9} &=25\\ \Leftrightarrow & & 25 &=25\\ \end{align}$

Zahlenrätsel

Aufgabe 3: Finde die gesuchte Zahl

Wenn man $12$ mit dem Doppelten einer Zahl addiert, so erhält man das Vierfache der gesuchten Zahl. Stelle eine geeignete Gleichung auf und gib die gesuchte Zahl an.

Hinweis

Zunächst übersetzen wir die Informationen aus der Aufgabenstellung in eine mathematische Schreibweise:

Das Doppelte einer Zahl: $2x$

$12$ mit dem Doppelten einer Zahl addieren: $2x+12$. Dies wird die linke Seite der Gleichung bilden.

Das Vierfache der gesuchten Zahl: $4x$. Dies ist die rechte Seite der Gleichung.

Wir erhalten also die Gleichung: $2x+12=4x$.

Um das gesuchte $x$ zu finden, müssen wir die Gleichung lösen, indem wir sie nach $x$ umstellen. Achte darauf alle Umformungen immer auf beiden Seiten der Gleichung durchzuführen.

$\begin{align}& & 2x+12 & = 4x & &\mid -2x\\ \Leftrightarrow & & 12 & = 2x & &\mid :2\\ \Leftrightarrow & & 6 & = x \end{align}$.

Die gesuchte Zahl ist $6$.

Aufgabe 4: Alter der Mutter

Die Mutter von Leon ist $3$-mal so alt wie er. In $12$ Jahren wird sie doppelt so alt sein wie Leon. Wie alt sind Leon und seine Mutter heute?

Beachte, dass sich das doppelte Alter auf das Alter in $12$ Jahren bezieht.

Leon ist $12$ Jahre alt und seine Mutter ist $36$ Jahre alt.

Rechnen mit Gleichungen im Sachzusammenhang

Beispiel 2: Titel

Beispiel

Aufgabe #: Volleyballfeld abstecken

Nick und Tom sollen für ein Sportfest ein Volleyballfeld abstecken. Dafür sollen sie ein $66$ m langes Seil und sechs Pfosten verwenden. Für das Umwickeln aller Pfosten werden insgesamt drei Meter Seil benötigt. Das Spielfeld soll aus zwei quadratischen Flächen bestehen. Wie lang ist eine Seite von einer der quadratischen Flächen, wenn man davon ausgeht, dass Nick und Tom das gesamte Seil benutzen?

Um die Gleichung aufzustellen, benötigst du den Umfang des Spielfeldes.

Benutze die Skizze, um einen Term für den Umfang des Spielfeldes aufzustellen.

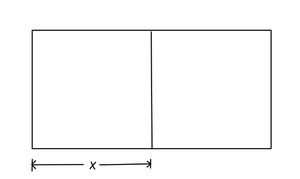
Skizzierung des Volleyballfeldes

Beachte, dass zusätzlich Seil für das Abspannen an den Pfosten benötigt wird.

Die gesuchte Seitenlänge bezeichnen wir mit $x$.

Skizzierung des Volleyballfeldes

Den Umfang des Spielfeldes erhalten wir durch den Term $7x$.

Wir erhalten die Gleichung: $7x+3=66$, da insgesamt $66$ Meter Seil zur Verfügung stehen und drei Meter Seil für die Abspannung an den Pfosten benötigt werden.

Diese Gleichung können wir lösen:

$\begin{align} & & 7x+3 &=66 & &\mid -3\\ \Leftrightarrow & & 7x &=63 & &\mid :7\\ \Leftrightarrow & & x &=9 \end{align}$.

Probe:

$\begin{align} & & 7 \cdot 9 +3 &=66\\ \Leftrightarrow & & 63 + 3 &=66\\ \Leftrightarrow & & 66 &=66\\ \end{align}$

Eine Seite ist $9$ m lang.

Aufgabe #: Getränkelager füllen

In einem Lager eines Restaurants sollen möglichst viele 35 cm hohee Getränkekisten übereinander gestapelt werden. Die Raumhöhe beträgt 2,10 m.

a) Beschreibe die Stapelhöhe durch einen Term. b) Wie viele Getränkekisten können übereinander gestapelt werden?

c) In dem Lager, mit einer Grundfläche von 10x10 m werden zurzeit auch Tische abgestellt. Jeder Tisch hat eine Grundfläche von 1 m² und eine Höhe von 90 cm. Wie viele Getränkekisten finden im Lager Platz, wenn dieses bereits durch 10 Tische belegt ist?

Inhalt des Tipps

Inhalt des Tipps.