Digitale Werkzeuge in der Schule/Fit für VERA-8/Lineare Funktionen

Info

In diesem Lernpfadkapitel hast du die Möglichkeit, dein Wissen über lineare Funktionen zu gebrauchen, zu erweitern und dein Verständnis zu vertiefen. Das Kapitel gibt dir eine Übersicht über die Zusammenhänge zwischen linearen Funktionen, die darauf liegenden Punkte und über die Gleichungen und Graphen linearer Funktionen.

• Orangene Aufgaben dienen der Wiederholung und Vertiefung.
• Blaue Aufgaben sind Aufgaben mittlerer Schwierigkeit.
• Grüne Aufgaben sind Knobelaufgaben.

Wiederholung: Was ist eine Funktion?

Aufgabe: Lückentext

Zur Einführung in das Thema der linearen Funktionen wiederholen wir zunächst, was eine Funktion überhaupt ist. Versuche dazu, den folgenden Lückentext auszufüllen, indem du die Wörter unter dem Text mit der Maus an die passende Stelle im Text ziehst. Anschließend kannst du deine Antworten überprüfen.

Eine Zuordnung $x \mapsto y$ heißt Funktion, wenn jedem $x$-Wert genau ein $y$-Wert zugeordnet wird.
Funktionen werden häufig mit $f$ bezeichnet.
Durch eine Funktion $f$ wird einer Variablen $x$ ein Funktionswert $f(x)$ zugeordnet.
Wenn es einen Term zur Berechnung der Funktionswerte gibt, dann nennt man ihn den Funktionsterm
und die zugehörige Gleichung heißt Funktionsgleichung.
Stellt man die Zahlenpaare $(x,y)$ als Punkte $P(x|y)$ in einem Koordinatensystem dar, so erhält man den Graphen der Funktion.

Übung: Überprüfe nun, ob die folgenden Zuordnungen eine Funktion beschreiben.

Überprüfe, ob bei der jeweiligen Zuordnung jedem $x$-Wert auch wirklich genau ein $y$-Wert zugeordnet wird. Bei den Fragen stellt jeweils das erste Wort der Zuordnung den $x$-Wert und das zweite Wort den $y$-Wert dar.

1.) Haus $\mapsto$ Adresse (Ja, die Zuordnung beschreibt eine Funktion.) (!Nein, die Zuordnung beschreibt keine Funktion.)

Da jedem Haus immer genau eine Adresse zugeteilt wird, beschreibt diese Zuordnung eine Funktion.

2.) Mutter $\mapsto$ Kind (!Ja, die Zuordnung beschreibt eine Funktion.) (Nein, die Zuordnung beschreibt keine Funktion.)

Diese Zuordnung beschreibt keine Funktion, da nicht jede Mutter genau ein Kind hat, sondern auch mehrere Kinder haben kann.

3.) Zahl $\mapsto$ Quersumme der Zahl (Ja, die Zuordnung beschreibt eine Funktion.) (!Nein, die Zuordnung beschreibt keine Funktion.)

Die Quersumme einer natürlichen Zahl ist die Summe ihrer einzelnen Ziffern. Zum Beispiel ist die Quersumme von $251$ gleich $8$, da $2+5+1=8$.

Da jede natürliche Zahl also genau eine Quersumme hat, ist die Zuordnung eine Funktion.

Lineare Funktionen erkennen

Erklärungstext

Merke

Wichtigste Infos zu linearen Funktionen. (Merkkästchen)

Aufgabe 1

Graphen zuordnen, ob lineare Funktion, keine Funktion (oder andere Funktion)

Graph einer linearen Funktion

Aufgabe 2

Zeichne die folgenden Graphen in dein Heft:

a.) $f(x)= 2x- 1$

b.) $f(x) = -3x+ 3$

c.)$f(x)= - 5/6x+ 2,5$

Es gibt zwei mögliche Wege einen Graphen zu zeichnen. Entweder du betrachtest m und b von der Funktionsgleichung $f(x)= mx+b$ genauer. Dieses Verfahren wird dir bei der Möglichkeit 1 genauer erläutert. Oder du setzt Punkte in die Funktionsgleichung ein. Die Möglichkeit 2 zeigt dir hierzu ein Beispiel.

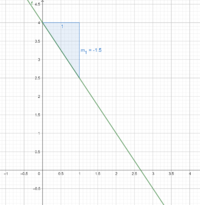
Betrachten wir als Beispiel die Funktionsgleichung $f(x)= -1,5x+4$.

Dabei gibt b=4 den Schnittpunkt mit der y- Achse im Koordinatensystem an. Wir wissen also, dass der Graph der Funktion durch den Punkt (0,4) verläuft.
Nun betrachten wir die Steigung welche durch m= - 1,5 gegeben ist. Du kannst dann vom Punkt (0,4) eine Einheit nach rechts und 1,5 nach unten gehen, weil die Steigung negativ ist.

( An dem Punkt könntest du, wenn dir 1,5 nicht so gut passt, auch ein Vielfaches nehmen. Du darfst dann aber nicht vergessen auch zunächst das Vielfache nach rechts zu gehen)

Betrachten wir erneut die Funktionsgleichung $f(x)= -1,5x+4$
Bei diesem Verfahren setzt du zwei verschiedene x-Werte in die Gleichung ein. Versuche einfache Werte zu wählen.
Du könntest zum Beispiel x=0 wählen. Dann wäre f(0)=-1,5*0+ 4= 0. Dies wäre der Punkt A(0,4).
Als nächstes wählst du eine andere Zahl, z.B. x=4. Dann wäre f(4)= -1,5*4+4= -6+4= -2. Dies wäre der Punkt B(4,-6).

Nun zeichne beide Punkte in ein Koordinatensystem ein. Verbinde diese mit einer Geraden durch die Punkte.

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

Aufgabe 3

Graphen mit Funktionsgleichungen verbinden

Bestimmung von Funktionsgleichungen

Merke: Das Steigungsdreieck

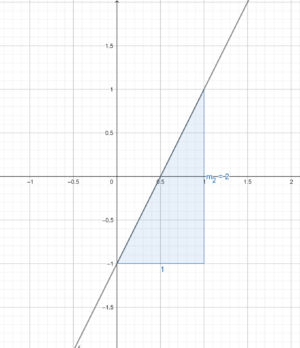
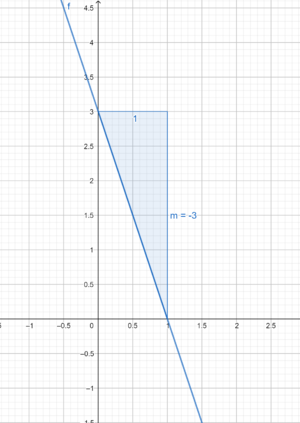
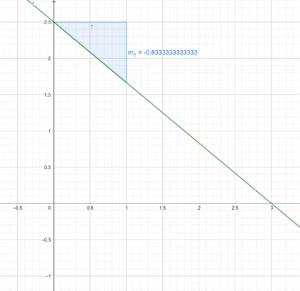
Die Steigung einer linearen Funktion erhält man mithilfe des Steigungsdreiecks, von welchem zwei Punkte auf dem Graphen liegen. Das Steigungsdreieck kennzeichnet, dass die Steigung dem Verhältnis des Höhen- und Längenunterschiedes beider Punkte entspricht.
Die Steigung berechnest du folgendermaßen:
1. Du suchst zwei beliebige Punkte $P(x_1|f(x_1))$ und $Q(x_2|f(x_2))$, die auf dem Graphen der Funktion liegen.
2. Um den Höhenunterschied der Punkte zu bestimmen, benötigt man die y-Koordinaten der Punkte P unc Q: Höhenunterschied: $f(x_2)-f(x_1)$
3. Um den Längenunterschied der Punkte zu bestimmen, benötigt man die x-Koordinaten der Punkte P und Q: Längenunterschied: $x_2-x_1$
4. Für die Steigung der Geraden gilt dann: $\frac{f(x_2)-f(x_1)}{x_2-x_1}$

Aufgabe: Funktionsgleichung mit Hilfe von zwei Punkten bestimmen

a) b) c) d) Wertetabelle

Überlegt euch, welche Infos ihr habt. (Platzhalter)

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

Aufgabe: Funktionsgleichung mit Hilfe von einem Punkt und der Steigung bestimmen

Lösung

Liegen die Punkte auf dem Graphen?

Aufgabe 6

Puzzle oder Verbinden (o.Ä.) mit verschiedenen Funktionsgleichungen und verschiedenen Punkten

Anwendungsaufgaben/ Modellierungsaufgaben

Aufgabe: Abbrennen einer Kerze

Eine Kerze ist 1,5 Stunden nach dem Anzünden 12 cm und 3,5 Stunden nach dem Anzünden noch 6 cm hoch.

a) Warum handelt es sich hierbei um eine lineare Funktion?
b) Zeichne den Graphen der Zuordnung Zeit $\rightarrow$ Länge der Kerze.
c) Lies ab: Wie lang war die Kerze zu Beginn? Nach welcher Brennzeit ist sie nur noch 1,5 cm hoch? Wann ist sie abgebrannt?
d) Bestimme die Änderungsrate und gib die Funktionsgleichung in der Form $f(x)=mx+b$ an. Ermittle nun die gesuchten Werte aus c) mithilfe der Gleichung. Vergleiche.

Überlegt euch, welche Infos ihr habt. (Platzhalter)

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

Text zum Verstecken

b) ohne "Lies ab" sondern Lösungsweg frei wählbar, dann müsste c) aber anders formuliert werden.

Aufgabe: Weg zum Training

Johannes geht zu Fuß von zu Hause aus zur 6km entfernten Sporthalle zum Fußballtraining. Er geht relativ konstant mit 4 km/h. Pauk steht schon vor der Sporthalle. Er startet zur gleichen Zeit wie Johannes mit seinem Fahrrad und fährt ihm entgegen. Paul fährt mit einer konstanten Geschwindigkeit von 16 km/h. Beide nehmen den selben Weg. Wann und wo treffen sie sich?

Text zum Verstecken

Text zum Verstecken

Aufgabe: Handytarife

Maria möchte im Internet surfen und begutachtet die Tarife A, B und C.

Tarif A: Grundgebühr 5 € / Monat die ersten 5 Stunden frei, dann 1 Ct./min.
Tarif B: Grundgebühr 10 € / Monat die ersten 10 Stunden frei, dann 0,8 Ct./min.
Tarif C: Flat–Rate 40 € / Monat.

Maria surft im Durchschnitt zwei Stunden am Tag. (30 Tage /Monat).

a) Stellen Sie für jeden Tarif die Funktionsgleichung auf.
b) Zeichnen Sie die Funktionsgraphen in ein geeignetes Koordinatensystem.
c) Erklären Sie, was alles aus den Graphen ablesbar ist (Interpretation).
d) Berechnen Sie den günstigsten Tarif für Maria.
e) In welchem Punkt herrscht Kostengleichheit für Tarif A und B?
f) Ab welcher Surfzeit ist Tarif C der günstigste?

Text zum Verstecken

Text zum Verstecken