Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Steigung in einem Punkt - die Ableitung als Tangentensteigung
Inhaltsübersicht
a) Unterscheidung Tangente, Sekante und Normale - Aufgabe 1
b) Zuordnungsaufgaben bezüglich der Tangentensteigung - Aufgabe 2, 3, 4 und 5
c) Untersuchung einer Funktion - Aufgabe 6, 7, 8 und 9
Aufgabe 1: Kannst du die Begriffe unterscheiden?
a) Unterscheidung Tangente, Sekante und Normale
b) Zuordnungsaufgaben bezüglich der Tangentensteigung
Aufgabe 2: Ordne die jeweilige Steigung den entsprechenden Punkten zu
Aufgabe 3: Die Steigung der Tangente in einem x-Wert
Aufgabe 4: Wahr oder Falsch?
Aufgabe 5: Memory. Wie fit bist du beim Behalten von Graphen und einer Steigung in einem Punkt?
c) Untersuchung einer Funktion
Aufgabe 6: Steigung und Koordinaten ablesen
Aufgabe 7: Raupenfahrt
<popup name="Lösung"> Die Steigfähigkeit der Raupe liegt mit 76% über der Steigung von 75%. </popup>
Aufgabe 9: Kann es in einem Punkt einer Funktion zwei oder mehr Tangenten geben?!
Error: www.geogebra.org is not an authorized iframe site.
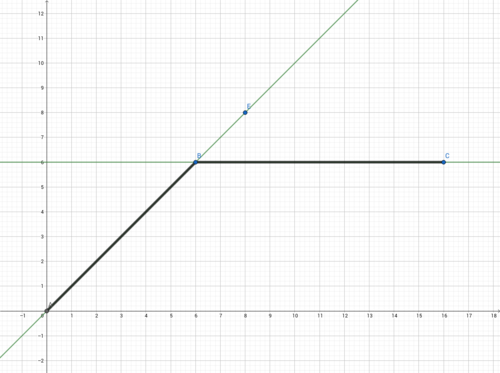
Verbinde mit Hilfe einer Strecke die Punkte (0|0), (6|6); (6|6), (16|6).
a) Welche Tangente(n) würdest du im Punkt P(6|6) einzeichnen?
b) Zeichne zu den jeweiligen Intervallen ([0;6] und [6;16]) die Steigung ein. Wie verläuft die Steigung und was passiert im Punkt P(6|6)?
<popup name="Lösung a)">
Im Punkt P(6|6) gibt es keine eindeutige Tangente. Je nachdem ob man die Steigung von links oder von rechts betrachte, erhält man eine andere, wie im Graph zu sehen ist.
</popup>
<popup name="Lösung b)">
Die Steigung verläuft im Intervall [0;6] und [6;16] linear. Jedoch gibt es
im Punkt P(6|6) einen Sprung. Hier ist die neue Funktion also nicht zusammenhängend (Sprungstelle) und daher auch nicht differenzierbar.
</popup>