Digitale Werkzeuge in der Schule/Ableitungen üben und vertiefen/Die Ableitung im Sachkontext anwenden

Merke

Die Aufgaben auf dieser Seite unterscheiden sich in ihrem Lernschwerpunkt und Schwierigkeitsgard:

• Für einen leichten Einstieg in die Sachkontexte befasse dich zunächst mit Aufgabe 1
• Falls du noch Probleme bei dem allgemeine Zuordnen der Ableitungsbegriffe zu den Anwendungskontexten hast konzentriere dich auf Aufgabe 2 & 3
• Komplexere Aufgaben befinden sich bei den Aufgaben 4 bis 7, wobei diese sich mit der Nummer in ihrer Schwierigkeit steigern. Solltest du schon sehr sicher mit den Aufgaben sein, gehe direkt zu Aufgabe 7

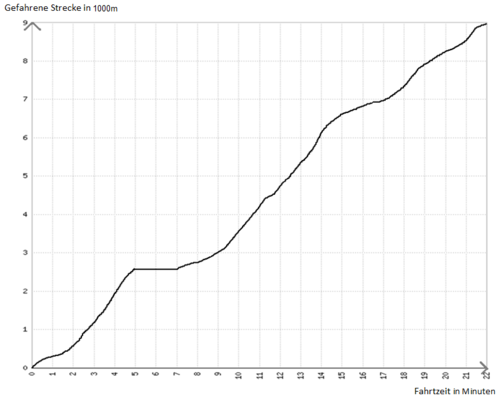
Aufgabe 1: Fahrtenschreiber

Aufgabe 1

Herr Müller arbeitet als Testfahrer bei einem Autohersteller. Seit zwei Tagen fährt und testet er einen neuen spritsparenden Prototypen.
Um genaue Informationen über die Fahrten zu erhalten, wurde ein Fahrtenschreiber in das Auto eingebaut. Heute morgen hat Herr Müller
ärgerlicherweise verschlafen und fährt eilig los, um pünktlich mit seiner Arbeit beginnen zu können.

Ausdruck des Fahrtenschreibers

a) Wie schnell ist Herr Müller auf seinem Weg zur Arbeit im Durchschnitt gefahren?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.

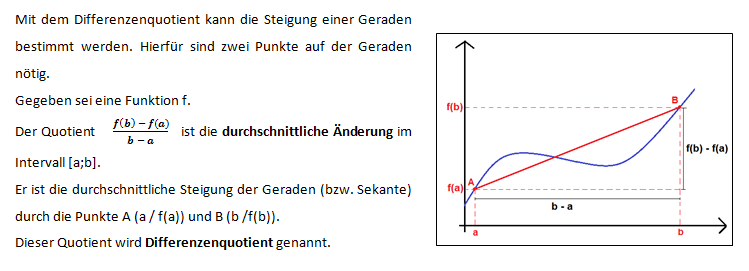
<popup name="Was genau ist der Differenzenquotient">

</popup>

<popup name="Lösung"> 24,5 km/h </popup>

b) Auf seinem Weg musst Herr Müller vor einer roten Ampel warten. Wann war das?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
<popup name="Lösung"> Er steht von Minute 5 bis 7 vor der Ampel und die Steigung des Graphen ist in dieser Zeit 0. </popup>

c) Beschreibe den Fahrtverlauf der ersten 12 Minuten stichpunktartig.
<popup name="Hilfestellung"> Schau dir den Graphen Stück für Stück an. Wie ist die Steigung (positiv, negativ, null) und was bedeutet dies im Sachzusammenhang?
<popup name="genauere Hilfestellung"> Eine positive Steigeung bedeutet, dass Herr Müller mit seinem Auto fährt. Ist die Steigung stark, so fährt er eine lange Strecke in kurzer Zeit, d.h. er fährt schnell.
Ist die Steigung schwach, fährt er langsam.
Ist die Steigung Null (siehe Aufgabe b)) steht das Atuo.
Eine negative Steigung macht in diesem Zusammenhang nicht so viel Sinn, da ein Fahrtenschreiber, selbst wenn Herr Müller nach Hause zurück fahren würde, aufschreibt, dass das Auto vorwärts fährt. </popup> <popup name="Lösung">

• Minute 0-2: Steigung ist relativ schwach. → Herr Müller fährt langsam
  
• Mintuen 3-5: etwas stärkere Steigung → Herr Mülelr fährt schneller
  
• Minute 5-7: Steigung ist Null → Herr Müller steht mit seinem Auto (vor einer Ampel)
  
• Minute 7-12: Steigung nimmt zu → Herr Müller wird immer schneller </popup>
  

Aufgabe 2: Ballwurf

Aufgabe 2

Bei den Bundesjugendspielen der Klasse 9 wirft Lisa einen Ball. Die Flugkurve ihres Balls kann näherungsweise durch die Funktion $f(x)=-0,02x^2+1,2x+2,08$ beschrieben werden.

a) Den Flug des Balls kannst du unter folgendem Link genauer betrachten. Lass hierzu den roten Ball fliegen, indem du bei dem roten Ball auf play drücken. Die anderen Punkte solltest du nicht bewegen!

Error: www.geogebra.org is not an authorized iframe site.

b) Bestimme die Steigung des Balls an den verschiedenen Punkten der Flugkurve.

<popup name="Lösung"> bei A= 0,8; bei B=0; bei C=-0,8 </popup>

c) Ordne die mathematischen Begriffe und Interpretationen den Markierungen auf dem Graphen zu.

Die gelbe Markierung soll einen Bereich statt einen Punkt kennzeichnen.

Für die Zuordnung musst die verschiedenen Markierungen anklicken und anschließend eine der vorgeschlagenen Möglichkeiten auswählen.

<popup name="Lösung"> grüne Markierung bei x=0 --> Standpunkt des Werfers

rote Markierung bei x=0 --> Y-Achsenabschnitt

erste gelbe Markierung --> Bereich mit positiver Steigung (bis zum Hochpunkt steigt der Graph)

grüne Markierung in der Mitte --> Punkt an dem der Ball weder steigt noch fällt (Im Hochpunkt ist die erste Ableitung gleich null somit ist auch die Steigung gleich null)

rote Markierung bei (30/20) --> Hochpunkt

rote Markierung bei (30/0) --> X-Wert des Hochpunktes

zweite gelbe Markierung --> Bereich mit negativer Steigung (nach Erreichen des Hochpunktes fällt der Graph wieder)

grüne Markierung bei x=61,7 --> Der Ball berührt den Boden

rote Markierung bei x=61,7 --> Nullstelle </popup>
d) Fülle die Lücken, indem du die Aufgabe im Sachzusammenhang interpretieren.
<popup name="Lösung"> eine negative Steigung bedeutet, der Ball verliert an Höhe;

eine positive Steigung bedeutet, dass der Ball an Höhe gewinnt ;

Der Ball wird aus einer Höhe von 2,08m geworfen, dies kann man am Y-Achsenabschnitt ablesen.

Das Intervall geht von 0 bis 61,7. Denn Lisa wirft am Punkt x=0 und der Ball trifft nach 61,7m auf den Boden (diesen Wert erhälst du, indem du die Nullstellen berechnest.)</popup>

Aufgabe 3: Zuordnungen

Aufgabe 3

Ordne den Abbildungen oder Formeln die zugehörige Interpretation zu

Aufgabe 4: Baumwachstum

Aufgabe 4

Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe

Durch die Funktion f mit $f(t)=-0,0027*t^2+0,108*t+0,02$ wird das Wachstum einer Fichte in Abhängigkeit von der Zeit t (in Jahren) beschrieben. Dabei gibt f(t) die Wachstumsgeschwindigkeit in Metern pro Jahr an. Zum Zeitpunkt t=0 hat eine frisch eingepflanzte Fichte eine Höhe von ca. 20 cm.

a) Berechne den Funktionswert von f an der Stelle t=30 und interpretiere das Ergebnis im Sachzusammenhang.
<popup name="Lösung"> f(30)=0,83 Die Fichte wächst im 30. Jahr 83cm. </popup>

b) Bestimme rechnerisch das Alter, in dem die Fichte am stärksten wächst, und gib die größte Wachstumsgeschwindigkeit an. <popup name="Hilfestellung"> Überlege dir an welche besonderen Punkte man bei einem Funktion berechnen kann. Welcher dieser Punkte ist für die Aufgabe relevant? <popup name="weitere Hilfestellung"> Extrempunkt (Hochpunkt)
Ansatz: notwendige Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösung"> Der Hochpunkt liegt bei t=20 und die Wachstumsgeschwindigkeit beträgt 1,1 Meter/Jahr. </popup>

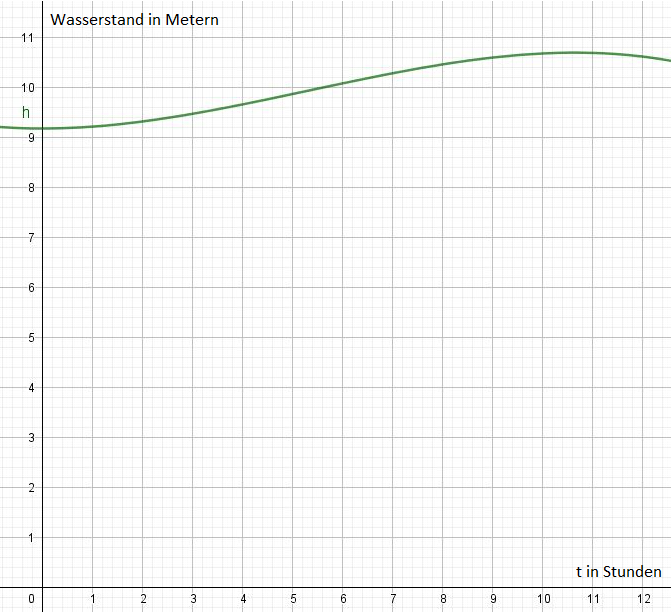
Aufgabe 5: Wasserstand

Aufgabe 5

Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe

In Nordrhein-Westfalen sind Hochwasser nichts Unbekanntes. Vorallem zwischen 1993 und 1995 gab es einige Rheinüberschwemmungen. In den ersten Tagen in 1995 ließen anhaltende Regenfälle und die beginnende Schneeschmelze den Rhein auf Rekordhöhe steigen. Bei dem Hochwasser wurde an einer Messstation zwölf Stunden lang der Wasserstand aufgezeichnet. Für 0 ≤ t ≤ 12, d.h. für den Beobachtungszeitraum von zwölf Stunden, stellt der Graph der Funktion h modellhaft die Höhe des Wasserstandes an dieser Messstation dar.

Hinweis:

• $h(t) = -0,0025t^3+0,04t^2+9,17$
  
• t = Zeit in Stunden seit dem Beobachtungsbeginn (27.01.1995 um 0:00)
  
• h(t) = Wasserstand in Metern

a) Berechne die Höhe des Wasserstandes um 7:30 Uhr. <popup name="Hilfestellung"> Setze für t 7,5 in die Funktion ein (=h(75)). </popup> <popup name="Lösung"> Rechnung: $h(7,5)=-0,0025*7,5^3+0,04*7,5^2+9,170$ =...≈ $10,37(m)$
Der Wasserstand liegt um 7:30 Uhr bei etwa 10,37 m. </popup>

b) Berechne die Geschwindigkeit, mit der der Wasserstand in den ersten acht Stunden des Beobachtungszeitraumes durchschnittlich anstieg.

<popup name="Hilfestellung"> Nutze den Differenzenquotienten.</popup>

<popup name="Lösung">Rechnung: $\frac{h(8)-h(0)}{8-0} = \frac{10,45-9,17}8 = 0,16$. Die Geschwindigkeit in den ersten achten Stunden betrug durchschnittlich 0,16 m/h. </popup>

c) Ermittle den Zeitpunkt,an dem der höchste Wasserstand an der Messtation erreicht wurde. Bereche auch den exakten Höchststand. <popup name="Hilfestellung"> Berechne den Extrempunkt (Hochpunkt).
<popup name="genauere Hilfestellung"> Nutze den Ansatz: hinreichende Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösungen"> Die Extremstelle liegt bei $t= \frac{32}3$ ≈ 10,67 (und t=0, entfällt, da h"(0)>0 und somit wäre es ein Tiefpunkt. (Dieser ist jedoch nicht gesucht.) Der Hochpunkt lautet H(32/3 | 5771/540). Der Wasserstand liegt bei etwa 10,69 m um etwa 10:40 Uhr. </popup>
d) Bestimme rechnerisch den Zeitpunkt, zu dem der Wasserstand am schnellsten anstieg, rechnerisch. <popup name="Hilfestellung"> Berechne die Wendestelle (Extremstelle der 1. Ableitung)
<popup name="genauere Hilfestellung"> Nutze den Ansatz: hinreichende Bedingung h"(t)=0 und h'"(t)≠0 </popup> <popup name="Lösungen"> Die Wendestelle liegt bei $t= \frac{16}3$. Daraus folgt, dass der Wasserstand nach 5 Stunden und 20 Minuten am schnellsten anstieg. </popup>

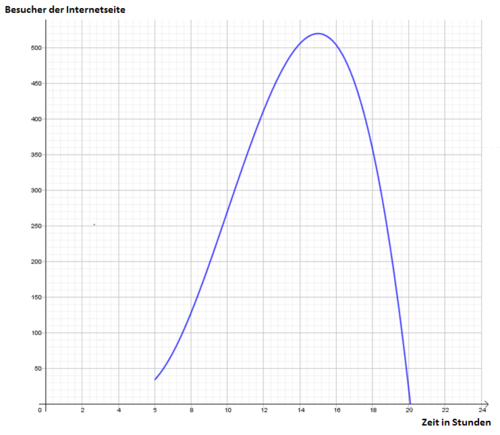
Aufgabe 6: Nutzungsverhalten

Aufgabe 6

In den letzten 24 Stunden hat eine Internetseite erfasst, wie viele Besucher die Seite hatte. Die Abbildung zeigt das Nutzungsverhalten von 6 bis 20 Uhr
Durch die Funktion $f(t)=-t^3+30*t^2-225*t+520$ für 6 ≤ t ≤ 20 wird das Nutzungsverhalten von 6 bis 20 Uhr dargestellt.

Nutzungsverhalten der Internetseite

a) Wie viele Besucher hatte die Internetseite um 10 Uhr?
Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="Lösung"> Es sind 270 Besucher </popup>

b) Wie viele Nutzer sind von 8 bis 10 Uhr im Durchschnitt pro Stunde dazu gekommen?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist.
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="Lösung"> Es sind 206 Nutzer pro Stunde </popup>

c) Zu welchem Zeitpunkt hat sich die Bescuherzahl durchschnittlich am stärksten geändert?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.
<popup name="genauere Hilfe"> Die Stelle an der ein Graph die stärkste Änderung (der Steigung) hat, heißt Wendestelle.
Um eine Wendestelle zu berechnen müssen folgende zwei Bedingungen erfüllt sein:
notwendige Bedingun: f´´(t) = 0
hinreichende Bedingung: f´´´(t) ≠ 0 </popup> <popup name="Lösung"> Bei t=10 </popup>

d) Zu welcher Uhrzeit haben die meisten Besucher die Internetseite besucht?

Hier kannst du deine Lösung eintragen und schauen ob sie richtig ist. Gib die Lösung mit einer Nachkommastelle an!
Bei Problemen, klicke auf die Glühbirne oben links.


<popup name="Lösung"> Bei t = 15 </popup>

Aufgabe 7: Konzertkarten

Aufgabe 7

Befasse dich mit der folgenden Anwendungsaufgabe. Nimm dazu dein Heft für die Rechnungen zur Hilfe

Eine Ticketagentur verkauft Karten für ein sehr begehrtes Konzert. Schon eine Stunde nach Freischaltung sind die Karten fast ausverkauft. Die Funktion f mit $f(t)=0,05*t^3-3*t^2+45,2*t$ beschreibt näherungsweise die Anzahl der Karten, die pro Minute zu einer bestimmten Zeit verkauft werden für die ersten dreißig Minuten des Verkaufs t=0 steht für den Zeitpunkt der Freischaltung der Hotline.

a) Zu welchem Zeitpunkt werden die meisten Karten pro Minute verkauft? <popup name="Hilfestellung"> Überlege dir welche besonderen Punkte du bei einer Funktion berechnen kannst. Welcher dieser Punkte ist für die Aufgabe relevant? <popup name="weitere Hilfestellung"> Extrempunkt (Hochpunkt)
Ansatz: hinreichende Bedingung h'(t)=0 und h"(t)<0 </popup> <popup name="Lösung"> Der Hochpunkt liegt bei t=29,933 </popup>
b) Wann im Verlauf der ersten Stunde nimmt die Anzahl der verkauften Karten am schnellsten ab? <popup name="Hilfestellung"> Überlege dir welche besonderen Punkte du bei einer Funktion berechnen kannst. Welcher dieser Punkte ist für die Aufgabe relevant? <popup name="weitere Hilfestellung"> Wendestelle (Extremstelle der 1. Ableitung)
Ansatz: hinreichende Bedingung h"(t)=0 und h'"(t)≠0 </popup> <popup name="Lösung"> Der Wendepunkt liegt bei t=20. </popup>