Herta-Lebenstein-Realschule/Lineare Funktionen im Aktiv-Urlaub/2) Lineare Funktionen
2.1) Lineare Funktionen erkennen und darstellen
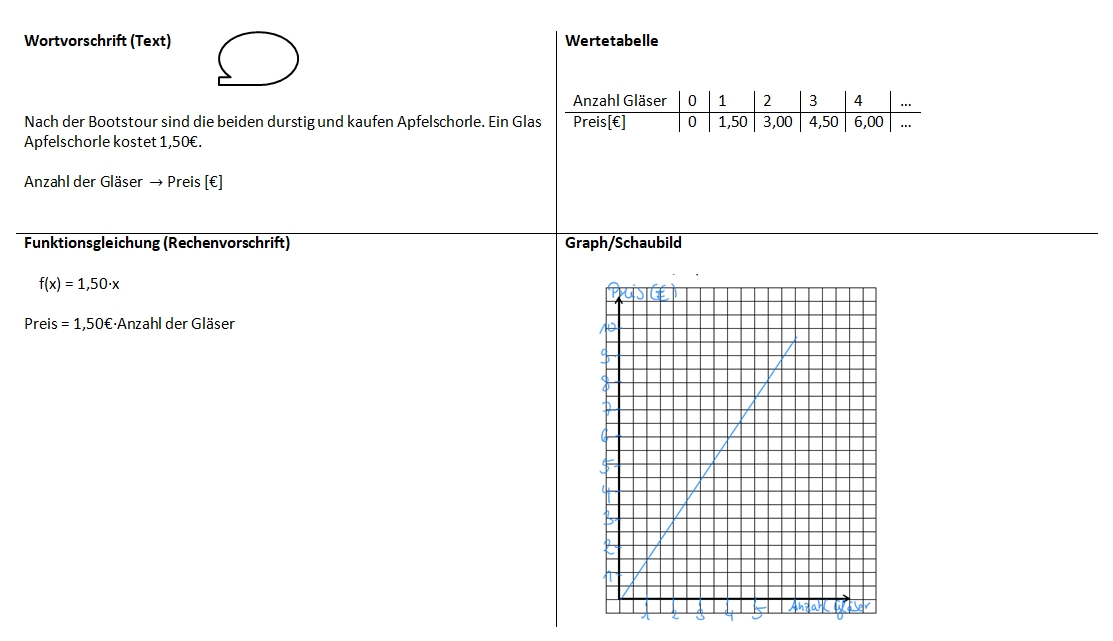
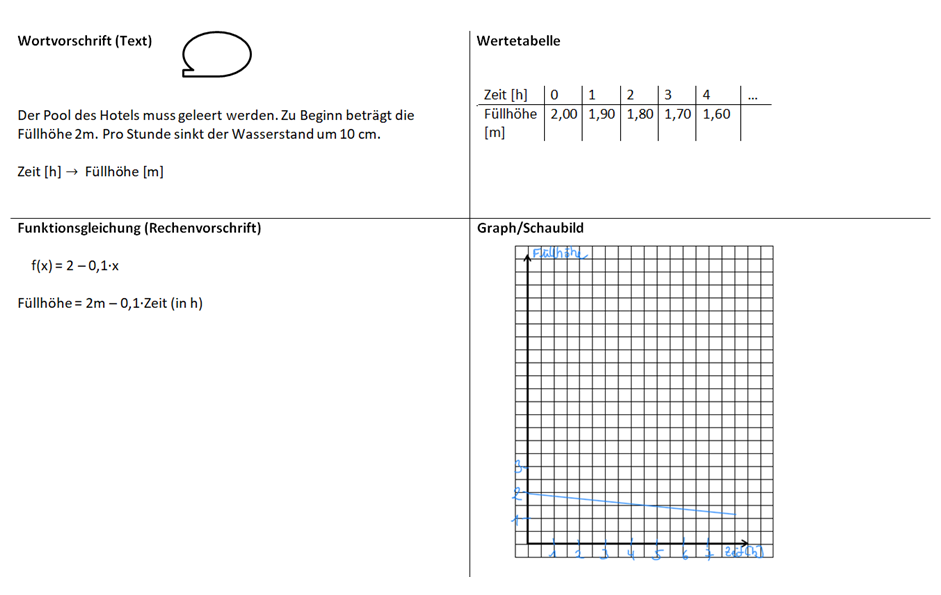
Im Aktiv-Urlaub warten verschiedene Aufgaben auf die Klassen.
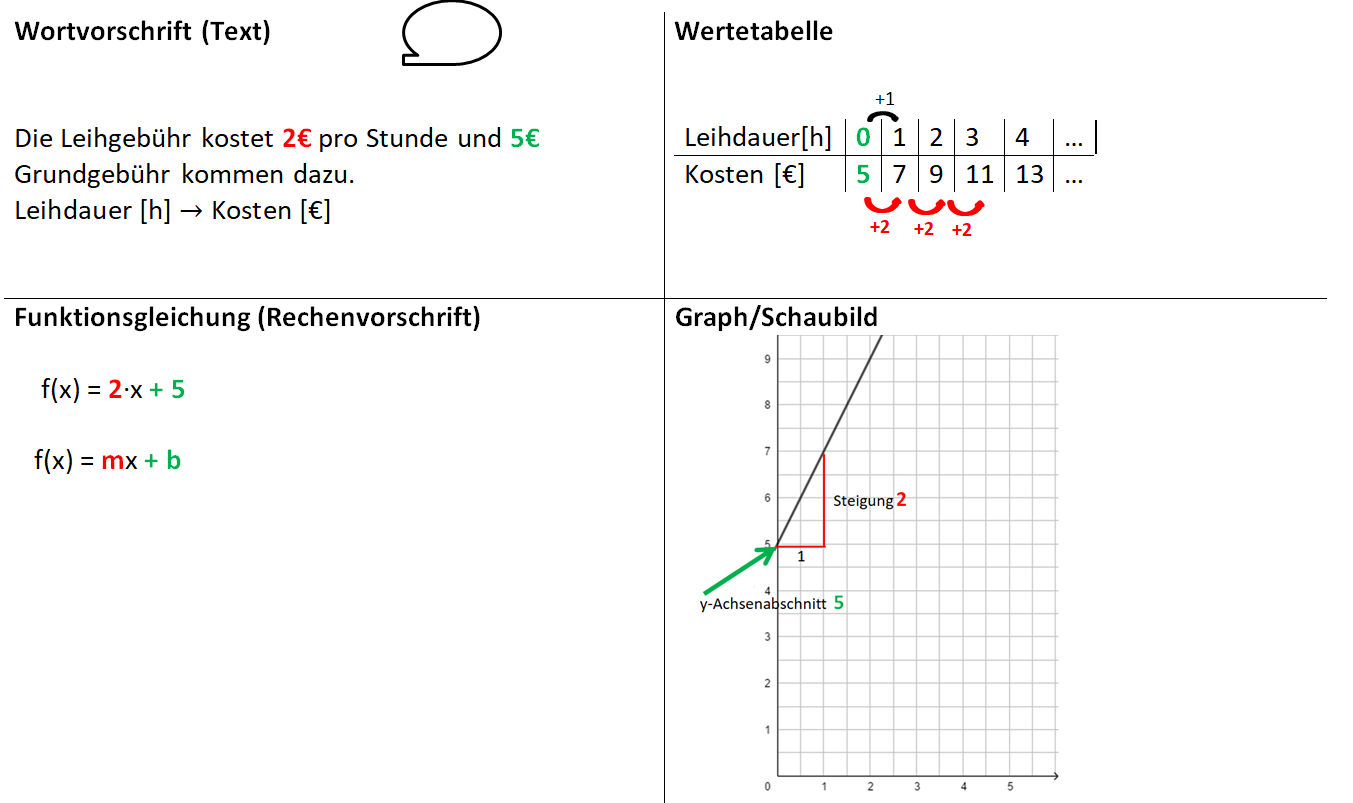
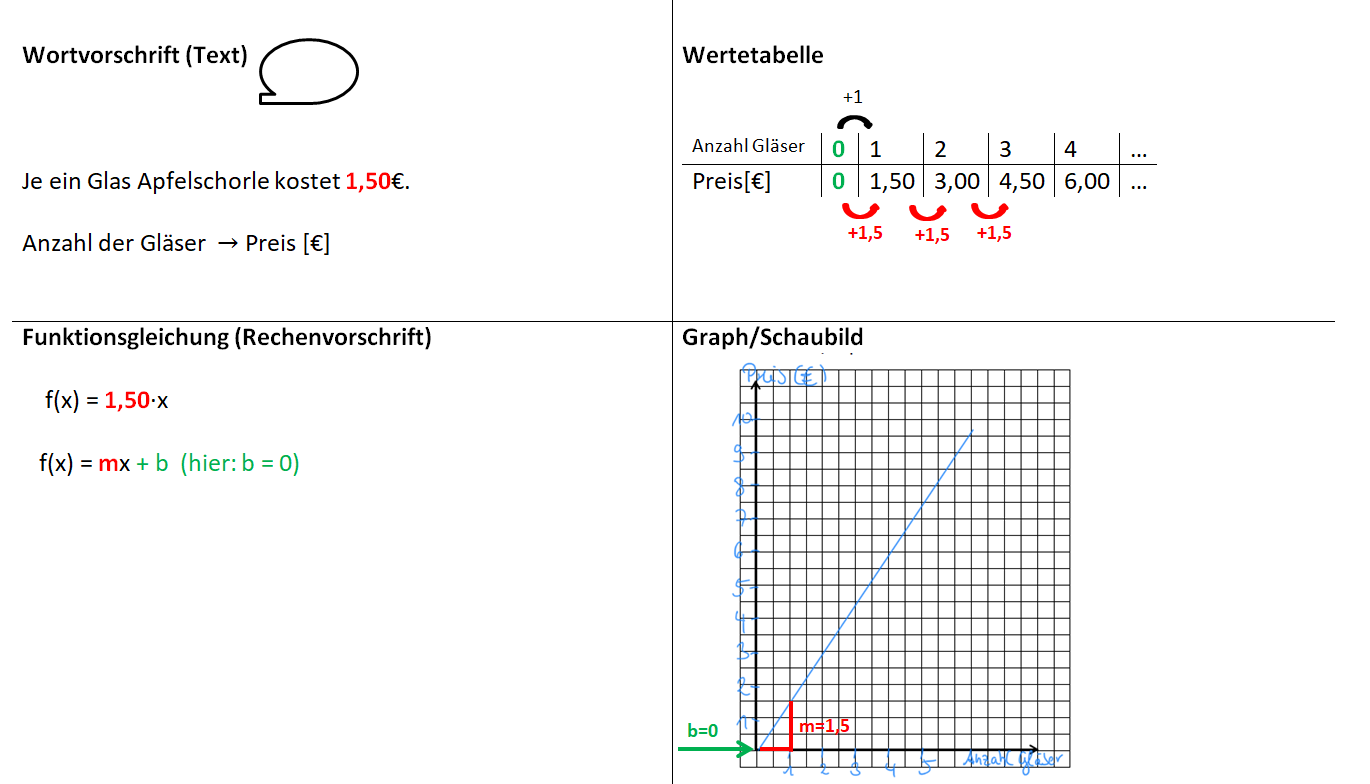
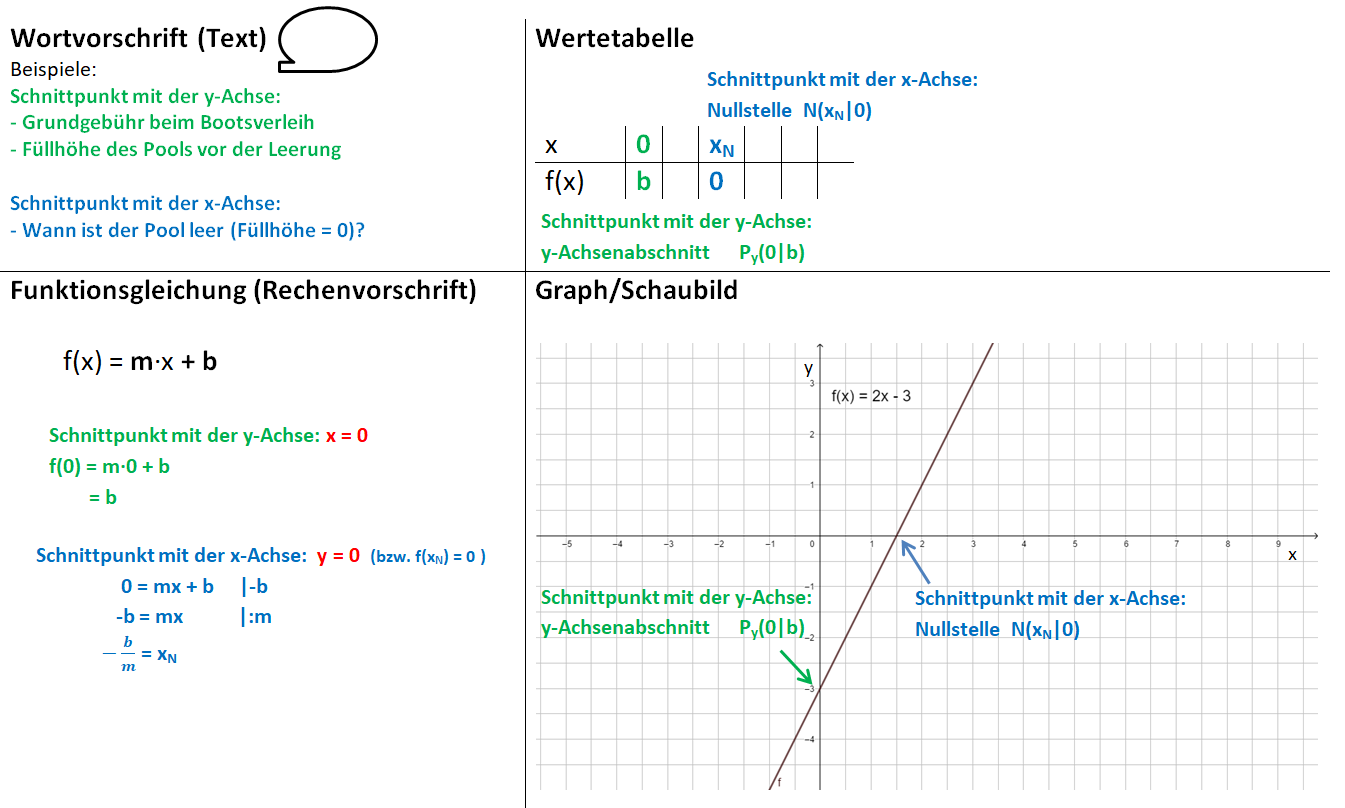
Die folgenden Erklärungen zu den Aufgaben 1, 2 und 3 zeigen, dass alle Funktionsgleichungen die Form f(x) = mx + b haben und die Funktionsgraphe immer Geraden sind.
Lineare Funktionen erkennen wir also in den verschiedenen Darstellungsmöglichkeiten wie folgt:
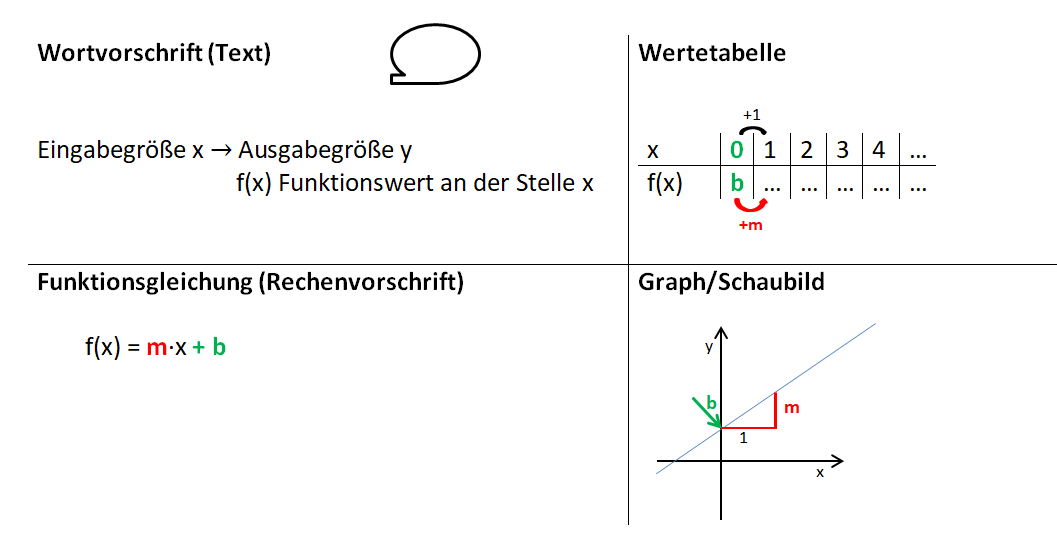
Diese Eigenschaften werden in folgendem Lied besungen (hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen). Du musst noch nicht jeden Zusammenhang, der hier genannt wird, verstehen. Vieles davon erarbeitest du auf den nächsten Seiten.
2.2) Zusammenhang zwischen Funktionsgleichung und Funktionsgraph
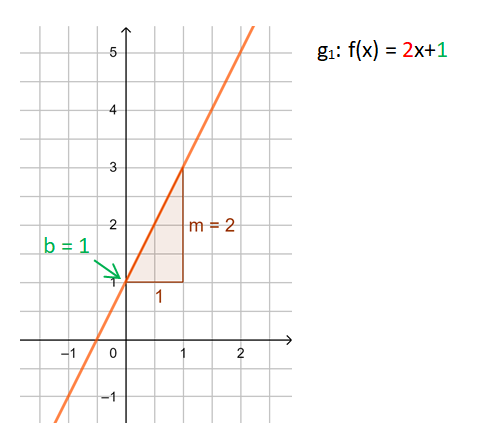
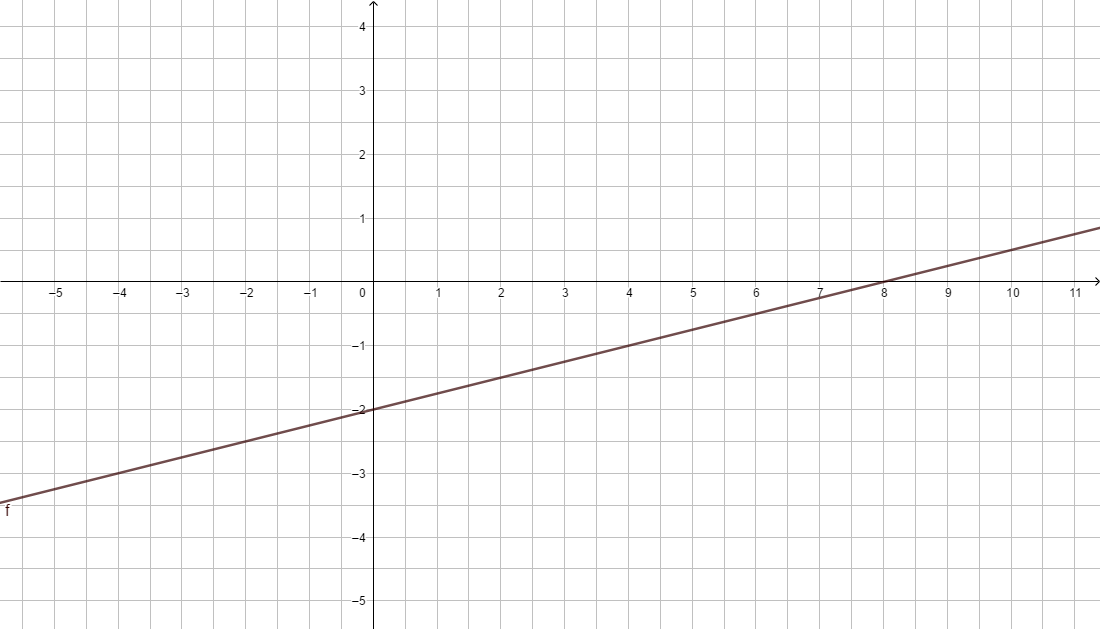
f(x) = mx + b Bedeutung von m und b für den Funktionsgraphen
Damit du einen Eindruck von der Bedeutung der Parameter m (Steigung) und b (y-Achsenabschnitt) der Funktionsgleichung linearer Funktionen f(x) = mx + b erhältst, verändere in der folgenden Animation mithilfe der Schieberegler die Größe von m und b. Notiere deine Beobachtungen stichpunktartig.

Übertrage die Merksätze in dein Heft:
Anschaulich vorstellen kannst du dir, dass die Funktion steigt, wenn der Wanderer den Berg hochsteigen muss.
Fällt die Funktion, "fällt" der Wanderer bergab.
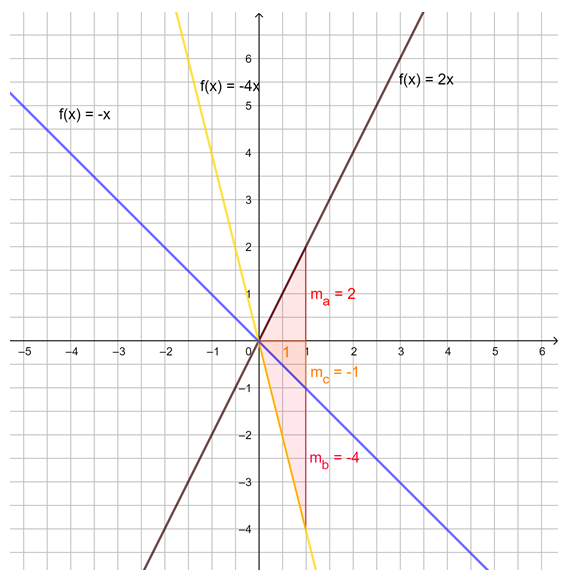
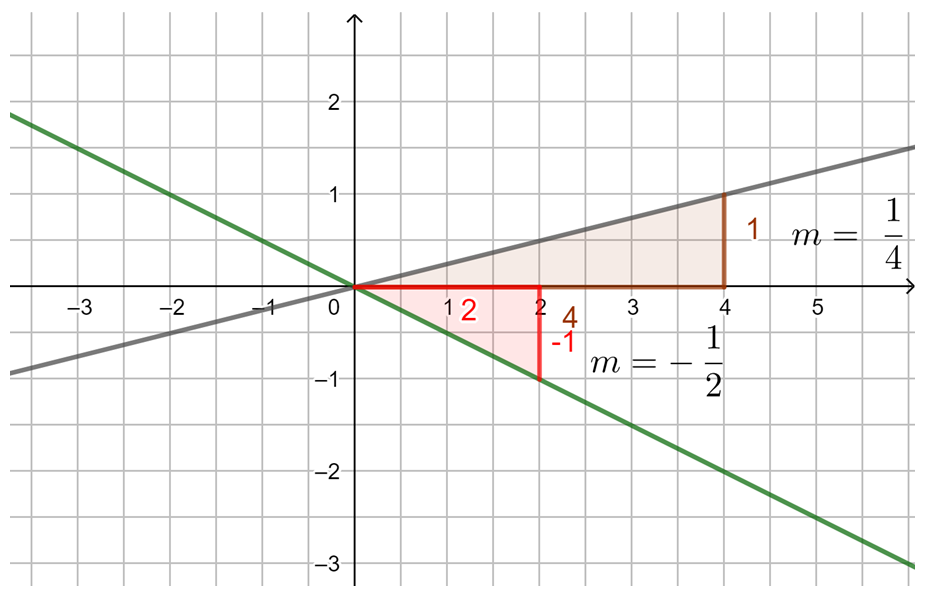
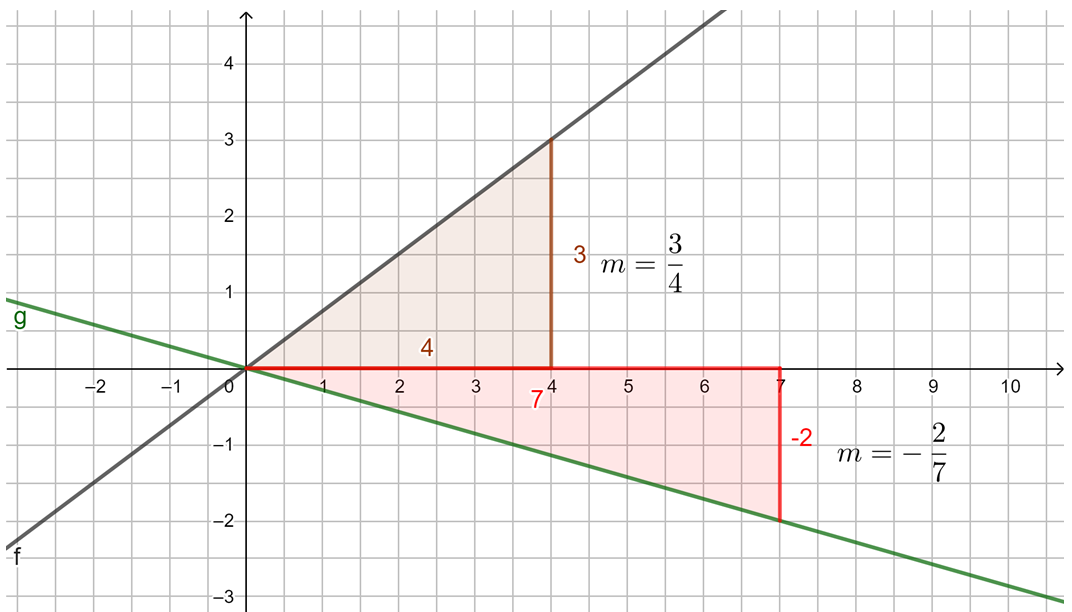
Die Steigung m linearer Funktionen
Untersuche mithilfe der Animation in GeoGebra die Steigung von Geraden. Du kannst mit den Schiebereglern m verändern. Außerdem kannst du das Steigungsdreieck durch Verschieben der Punkte A und B verändern. Beobachte, was geschieht. Probiere aus.

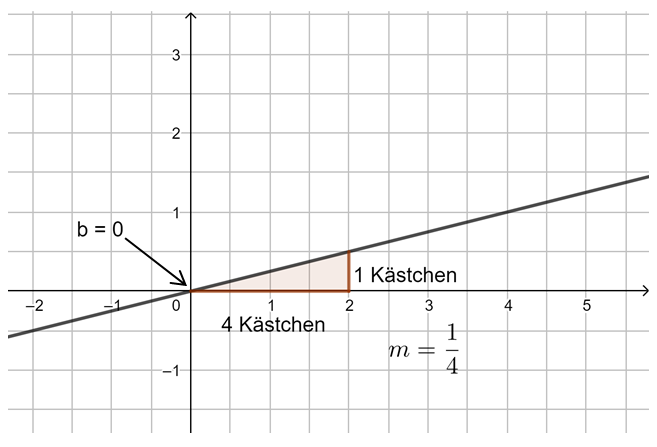
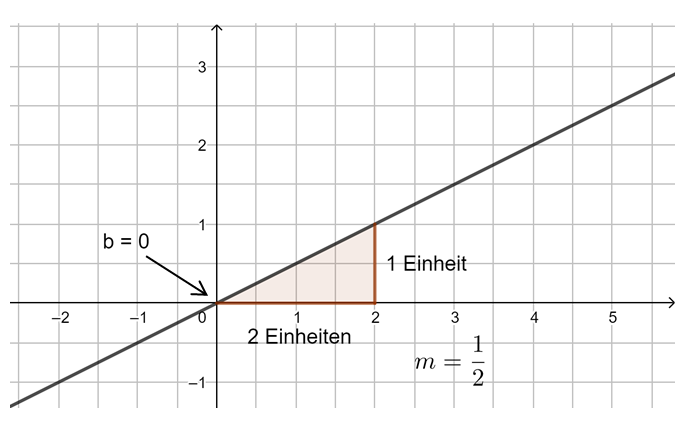
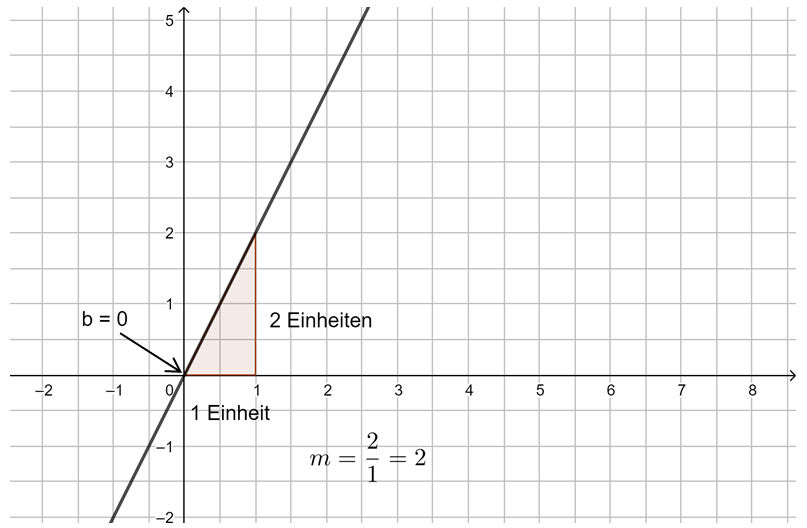
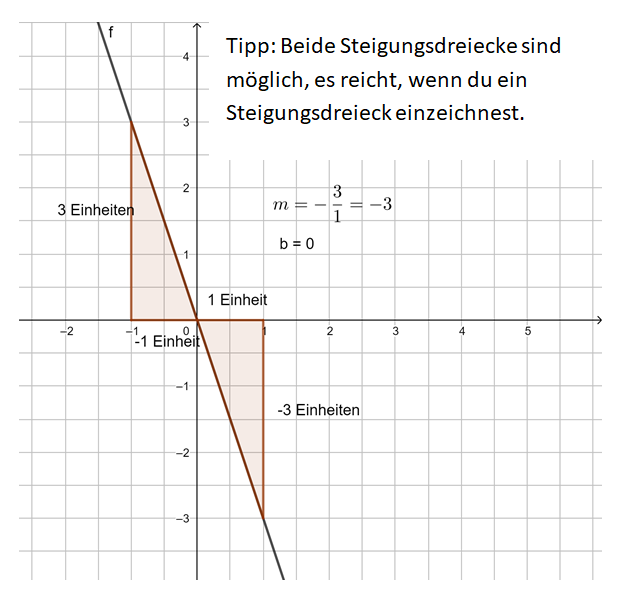
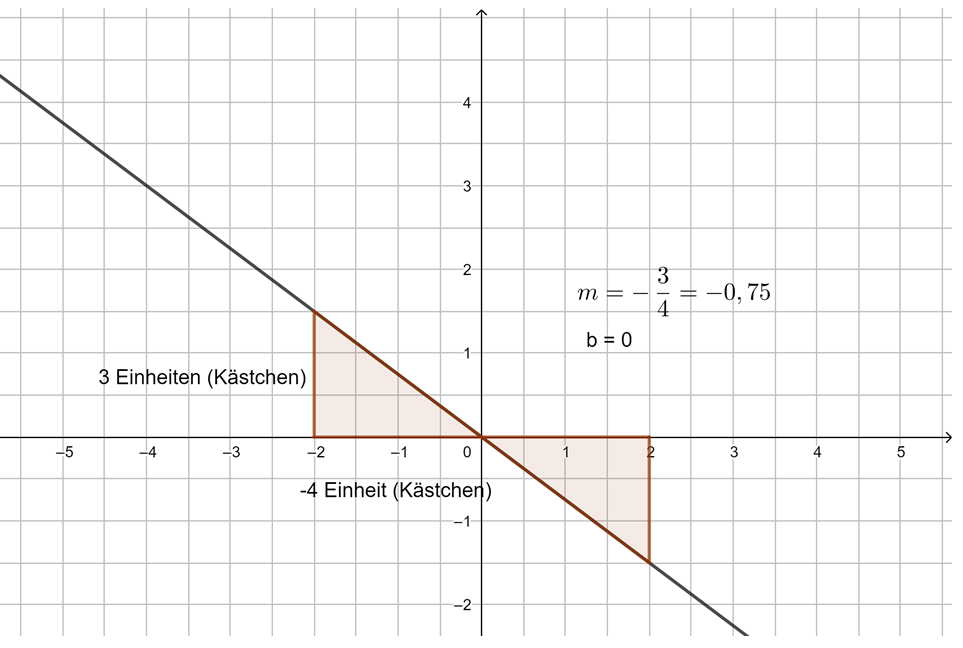
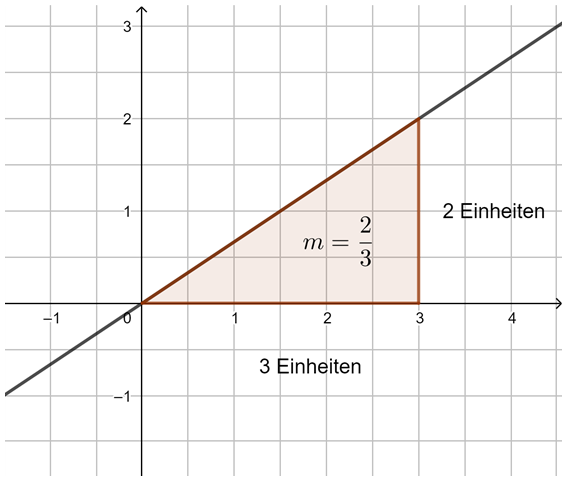
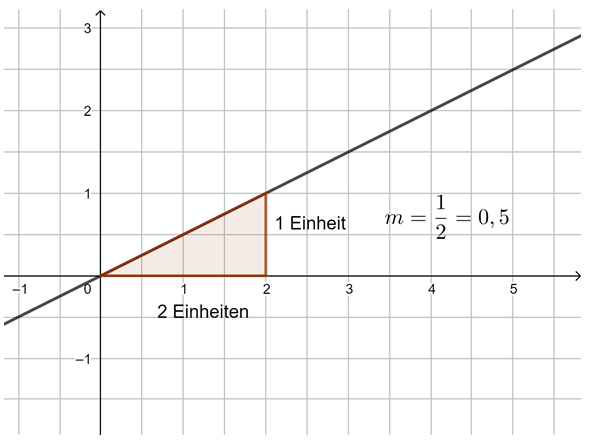
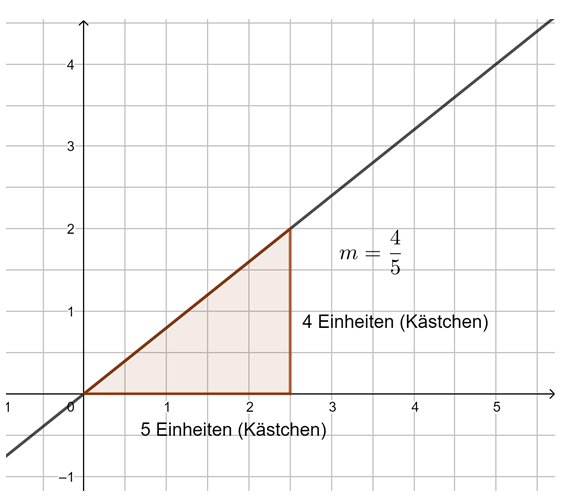
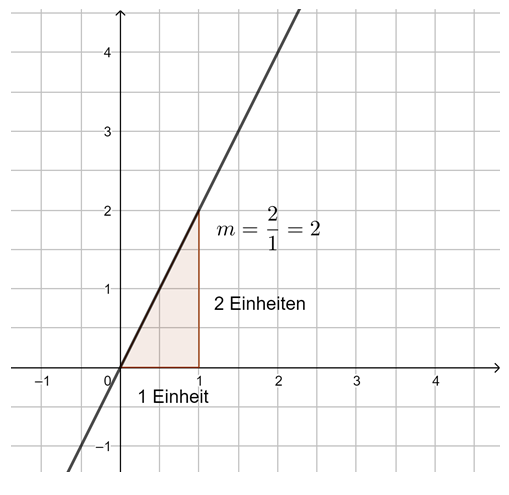
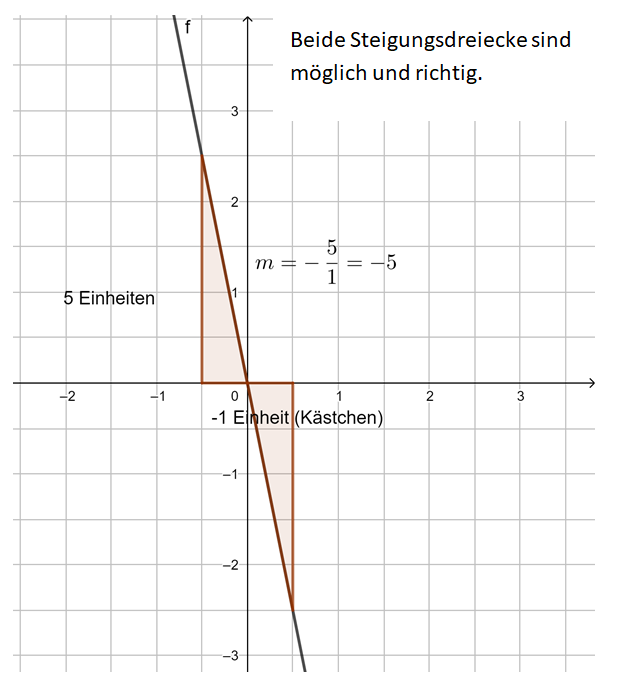
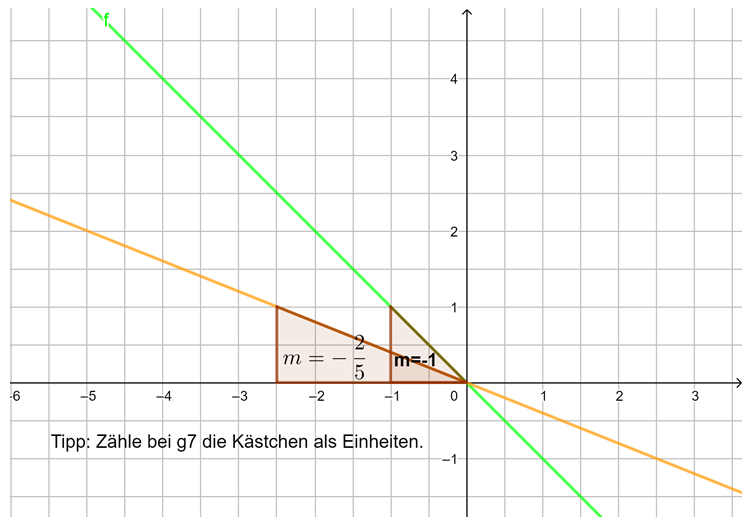
Beobachtung: Die Steigung m einer linearen Funktion können wir mit einem Steigungsdreieck ermitteln und darstellen. Dazu zeichnen wir von einem beliebigen Punkt auf der Geraden ein Dreieck zu einem anderen Punkt auf der Geraden, bei dem die eine Seite parallel zur x-Achse liegt und die andere parallel zur y-Achse. Gehen wir dabei genau 1 Einheit in x-Richtung, steigt (oder fällt) der y-Wert immer um den Wert m, die Steigung.
Egal, wie das Steigungsdreieck gezeichnet wird, der Quotient aus ![]() bleibt immer gleich, dies ist die Steigung m.
bleibt immer gleich, dies ist die Steigung m.
Schau dazu das nachfolgende Video zu Steigungsdreiecken an:
Von der Geraden zu Funktionsgleichung
Und nun noch einmal übersichtlich als Bild:
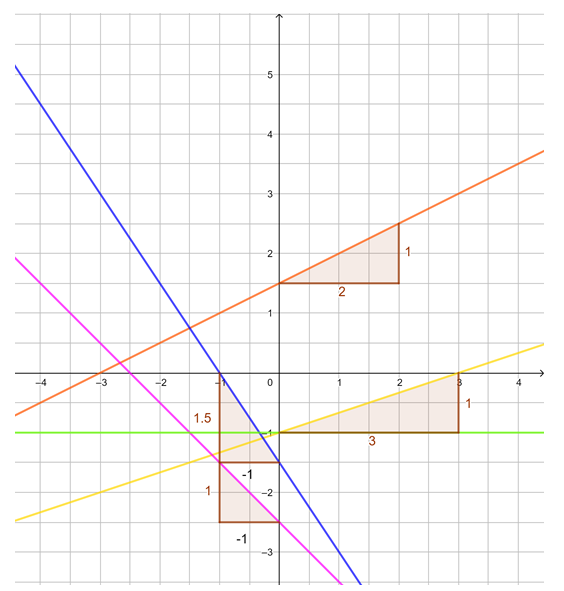
Öffne das GeoGebra-Applet zu S. 129 Nr. 2 und verändere den Wert des Schiebereglers b.
Öffne das GeoGebra-Applet zu S. 129 Nr. 4 und verändere den Wert des Schiebereglers m. Stelle m so ein, dass der Graph g1, g2,... entspricht. Die Funktionsgleichung wird dir angezeigt.
https://www.geogebra.org/classic/qfasm3egNutze auch hier das GeoGebra-Applet, um die Graphen nachzustellen und die Funktionsgleichung abzulesen
https://www.geogebra.org/classic/w8n4uabh
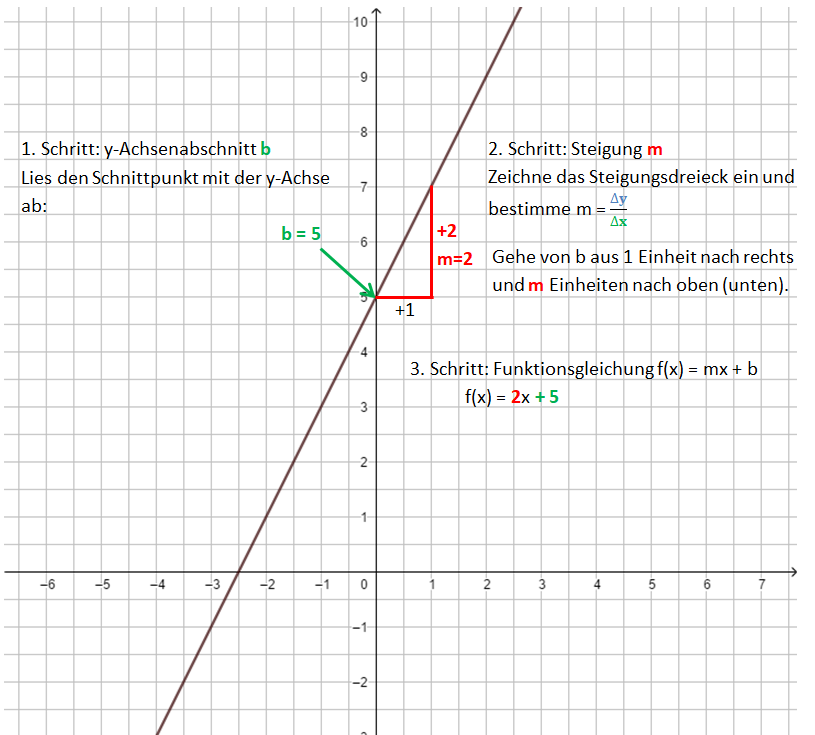
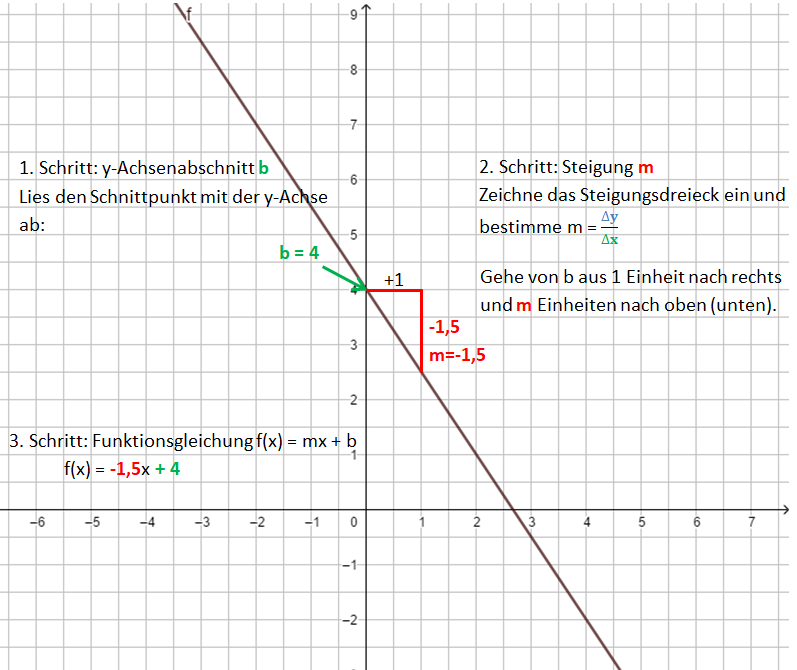
Von der Funktionsgleichung zur Geraden
Dabei gehst du ähnlich vor, wie beim Bestimmen der Funktionsgleichung.
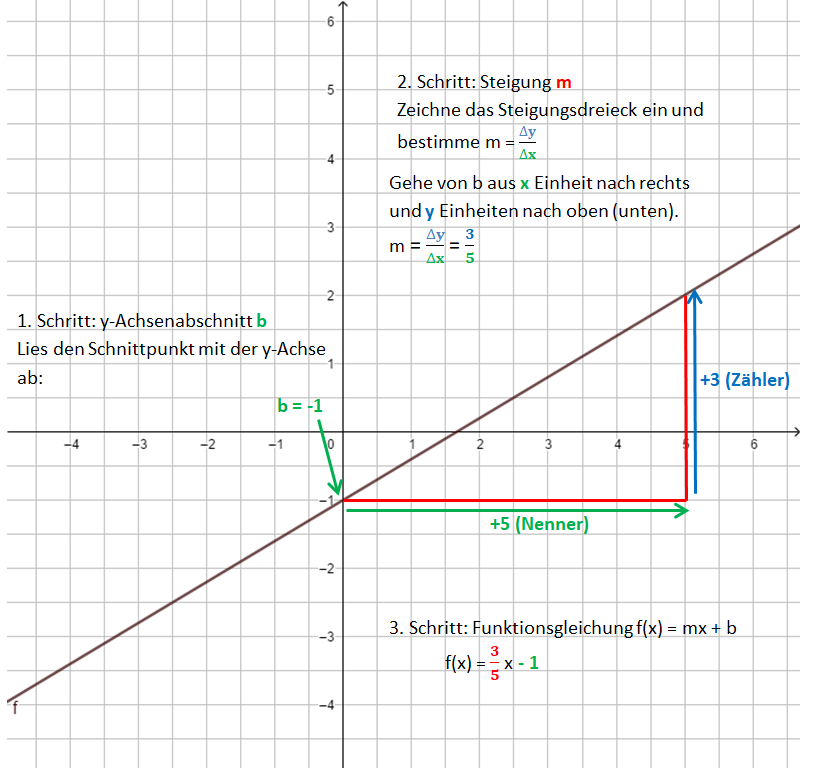
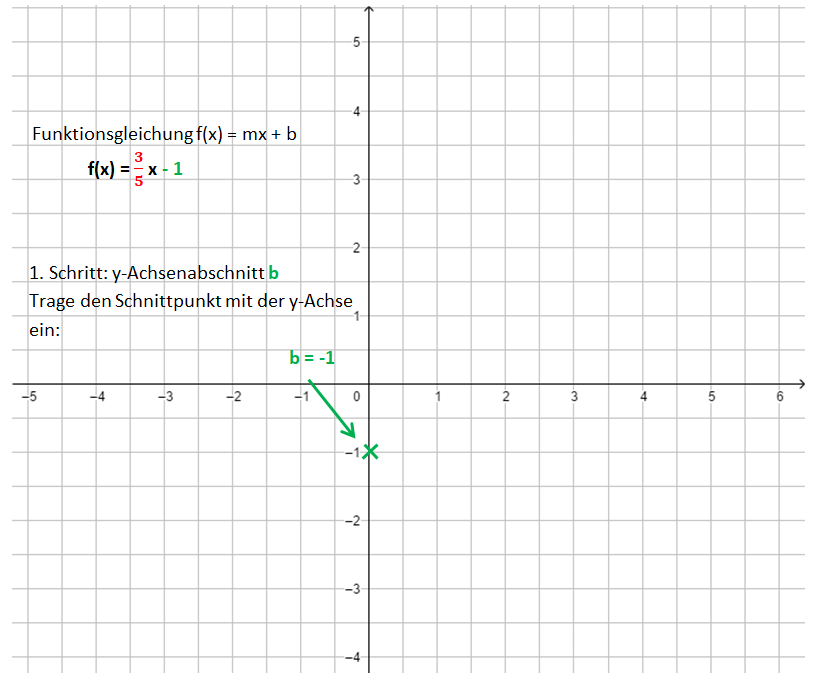
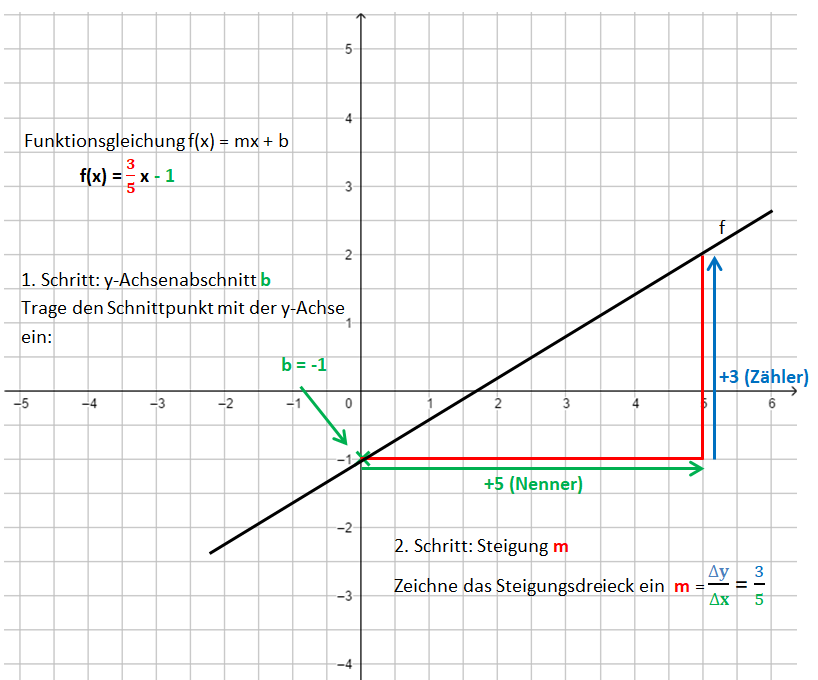
1. Schritt: Zeichne den y-Achsenabschnitt b ein: P(0|b)
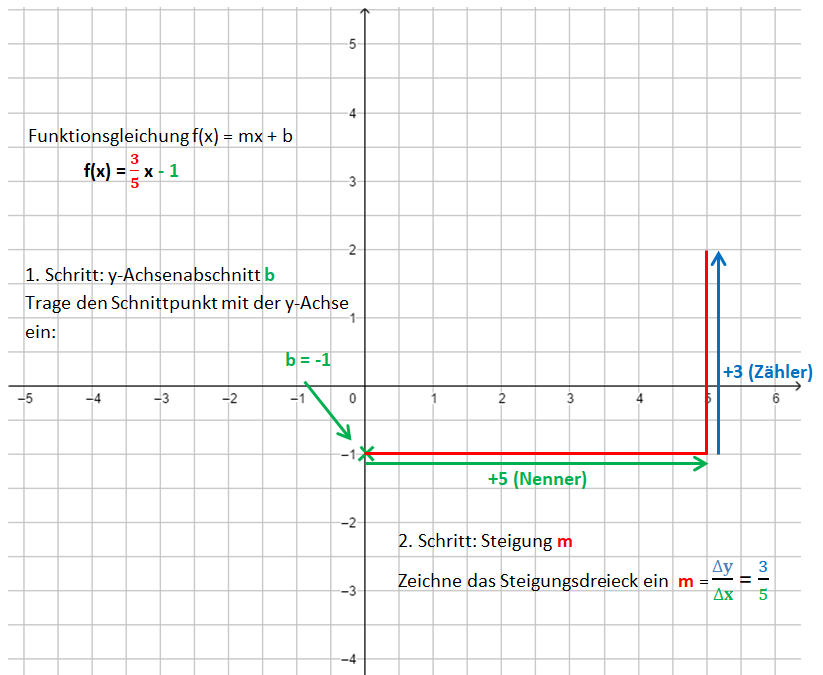
2. Schritt: Zeichne das Steigungsdreieck ein. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten).
3. Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Übertrage das Beispiel mit den Anmerkungen in dein Heft!
Die Videos zeigen das Vorgehen noch einmal:
Zeichne zuerst den y-Achsenabschnitt b ein, von hier aus zeichne das Steigungsdreieck. Prüfe deine Zeichnung mit GeoGebra.
https://www.geogebra.org/graphingStatt der Partnerarbeit erstelle eine Learningapp, in der den von dir gezeichneten Graphen die entsprechende Funktionsgleichung zugeordnet werden soll.
Wenn du für die Steigung einen Bruch wählst, kannst du ihn bei den LearningApps auch so schreiben, wie du es aus dem Unterricht kennst, indem du statt 2/3 folgendes schreibst: $$\frac{2}{3}$$
2.3) Zusammenhang zwischen Wertetabelle und Funktionsgleichung
Wiederholung: Erstellen einer Wertetabelle mithilfe der Funktionsgleichung
Du hast in den Einführungsbeispielen schon Wertetabellen erstellt. Schauen wir uns das Beispiel zum Bootsverleih noch einmal an. Die Funktionsgleichung lautet f(x) = 2x + 5
Um nun eine Wertetabelle zu erstellen, setze für x verschiedene Werte ein und berechne den zugehörigen y-Wert, den Funktionswert. Erinnerung: Werte von Termen berechnen (7. Klasse)

Das Video fasst das Vorgehen noch einmal zusammen:
Gib die Funktionsgleichungen bei GeoGebra ein und prüfe, ob die von dir errechneten Punkte auf dem Graphen der Funktion liegen.
https://www.geogebra.org/graphing
Punktprobe: Liegt der Punkt auf der Geraden?
Bei der Punktprobe entscheidest du rechnerisch, ob ein Punkt auf dem Funktionsgraphen liegt.
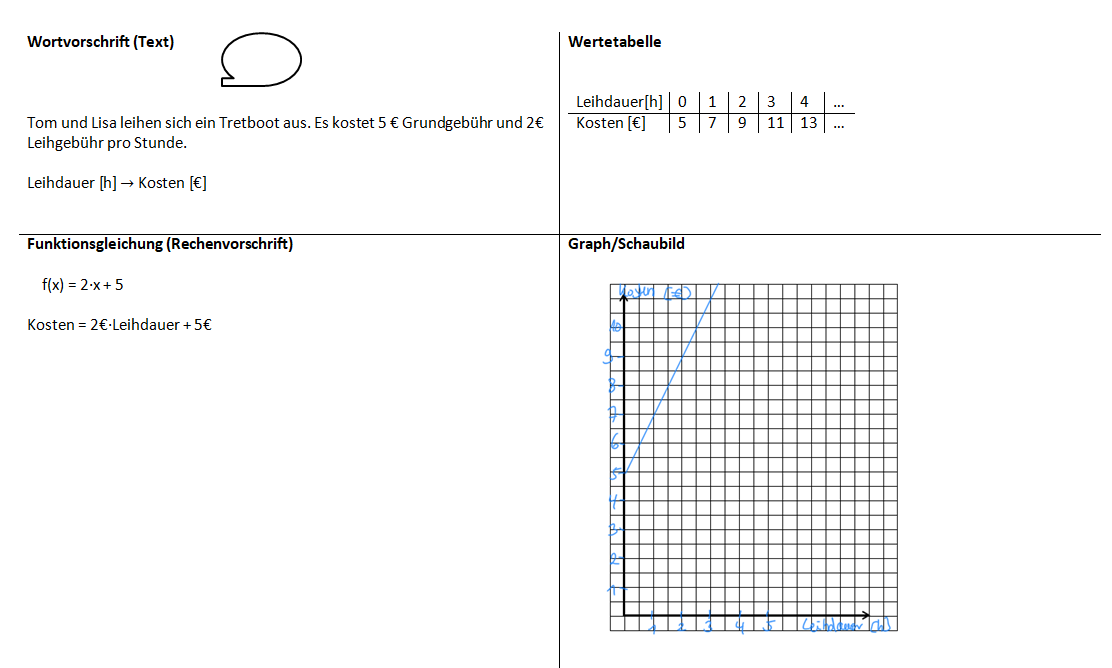
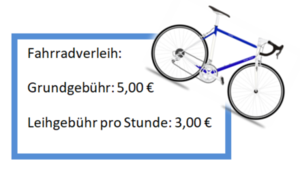
Tom und Lisa leihen für 3 Stunden ein Tretboot. Der Bootsverleiher rechnet den Preis 10€ aus. Kann das sein?
geg: Punkt A(3|10); Funktion f(x) = 2x + 5
ges: Liegt der Punkt A auf dem Graphen der Funktion?
In der Zeichnung erkennen wir sofort, dass dies nicht der Fall ist.
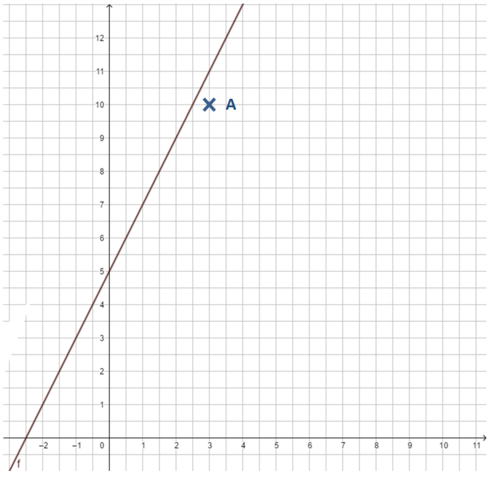
Gegeben ist die Funktionsgleichung y = 2x + 5. Liegt der Punkt A(3|10) auf dem Graphen der Funktion?
(Hier ist es leichter y statt f(x) zu schreiben, der Zusammenhang zu den Koordinaten des Punktes sind dann leichter zu erkennen.)
Idee: Setze die Koordinaten des Punktes in die Funktionsgleichung ein und prüfe, ob die Gleichung erfüllt wird.
y= 2x + 5 A(3|10)
10 = 2·3 + 5
10 = 6 + 5
10 = 11 (f)
Es ergibt sich eine falsche Aussage, die Gleichung ist nicht erfüllt, also liegt der Punkt nicht auf dem Graphen. Wir prüfen ebenso, ob der Punkt B(4|13) auf der Geraden liegt:
Punktprobe:
y = 2x + 5 B(4|13)
13 = 2·4 + 5
13 = 8 + 5
13 = 13 (w)
Es ergibt sich eine wahre Aussage, die Gleichung ist erfüllt, also liegt der Punkt auf dem Graphen.
Das folgende Video fasst noch einmal zusammen:
Fehlende Koordinate eines Punktes der Funktion berechnen
Du kannst mithilfe der Funktionsgleichung fehlende Koordinaten berechnen.
1. Möglichkeit: x-Koordinate ist gegeben
Tom und Lisa leihen ein Tretboot für 1,5 Stunden. Wie viel müssen sie bezahlen?
geg: x = 1,5 und f(x) = 2x+5
ges: zugehöriger y-Wert
Setze die x-Koordinate in die Funktionsgleichung ein und berechne: f(x) = 2x + 5
y = 2·1,5 + 5
= 3 + 5
= 8 P(1,5|8)
Sie müssen 8€ bezahlen.
2. Möglichkeit: y-Koordinate ist gegeben:
Tom und Lisa bezahlen 10 €. Wie lange haben sie das Tretboot ausgeliehen? geg: y = 10 und f(x) = 2x+5 ges: zugehörige x-Koordinate Setze die y-Koordinate in die Funktionsgleichung ein und löse nach x auf:
f(x) = 2x + 5
10 = 2x + 5 |-5
5 = 2x |:2
2,5 = x P(2,5|10)
Sie haben das Boot für 2,5 Stunden geliehen.
Aufstellen der Funktionsgleichung durch den Punkt P mit m oder b gegeben
Die vorangegangenen Übungen zur "Punktprobe" können dir helfen:
Sezte in die allgemeine Funktionsgleichung f(x) = mx + b die gegebenen Größen ein und löse nach der gesuchten Größe auf.Zu Nr. 9: Wenn die Gerade parallel zur Geraden von f(x)= 1,5x + 1 verläuft, haben die Geraden dieselbe Steigung! Also ist m = 1,5 gegeben. Außerdem hast du den Punkt P(2I6) gegeben. Gesucht ist b.
Setze die gegebenen Größen ein und löse nach b auf.
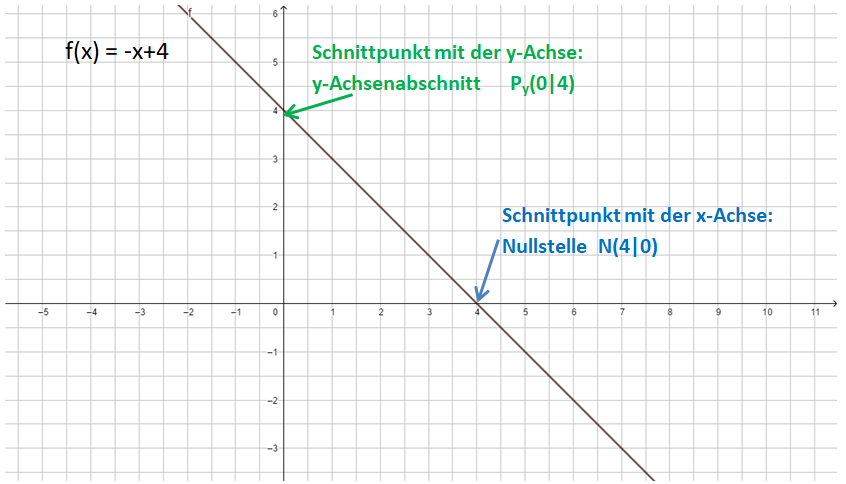
Schnittpunkte mit den Koordinatenachsen bestimmen
Nullstelle (Schnittpunkt mit der x-Achse): f(x) = 0, also -x+4 = 0
y-Achsenabschnitt (Schnittpunkt mit der y-Achse): x = 0, also f(0) = -0+4
Prüfe dein Ergebnis mithilfe von GeoGebra https://www.geogebra.org/graphing . Gib dort die Funktionsgleichung ein und vergleiche deine rechnerischen Lösungen mit dem Graphen. Wo schneidet der Graph die Koordinatenachsen?2.4) Lineare Funktionen im Aktivurlaub und andere Anwendungen
Es gibt Situationen in unserem Alltag, in denen sich Probleme oder Fragen mithilfe von linearen Funktionen beschreiben und lösen lassen. Solche Aufgaben nennen wir "Anwendungsaufgaben". Die Alltagssituation wird in ein mathematisches Modell übertragen, mit unserem Wissen zu den linearen Funktionen mathematisch gelöst und diese Lösung dann auf die Situation bezogen. Die nachfolgende Struktur hilft dir dabei:
Die Zuordnung lautet Zeit [Stunden] Kosten [€]
x gibt also die Zeit an, f(x) die Kosten.
Du benötigst für die Funktionsgleichung die Steigung m und den y-Achsenabschnitt b.
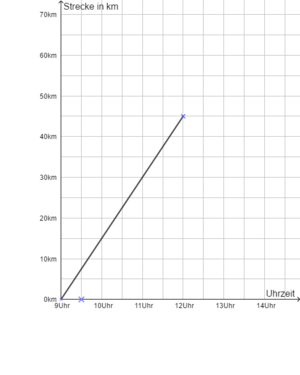
Die Steigung der Funktion ist m = 20, denn in 1 Stunde werden 20 km zurückgelegt.
Der y-Achsenabschnitt beträgt -10, da der Freund 0,5 Stunden später startet, in denen er 10 km zurückgelegt hätte.
Die Funktionsgleichung lautet f(x) = 20x-10, wobei x die Anzahl der Stunden (nach 9:00 Uhr) angibt.Der Punkt, wann die Freunde sich treffen, ist der Schnittpunkt der beiden Geraden. Hier haben beide Gruppen dieselbe Strecke zurückgelegt, das heißt, sie sind gleich weit gefahren und müssen sich demnach treffen.
Um zu berechnen, wann die Freunde sich treffen, berechne also den Schnittpunkt der Gerden. An dieser Stelle x haben sie dieselben y-Werte, sie sind gleich weit gefahren. Es gilt y = 15x und y=20x-10.
Löse die Gleichung 15x = 20x-10 nach x auf.
Für die Funktionsgleichung benötigst du die Steigung m und den y-Achsenabschnitt b. Wo findest du dies in der Wertetabelle? Den y-Achsenabschnitt liest du bei x=0 ab.
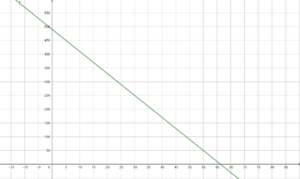
Die Steigung m findest du so: Wenn du bei x eine Einheit nach rechts gehst, gehst du m Einheiten nach oben oder unten. Wie groß ist also die Steigung hier?geg: x=6 Sekunden; f(x) = -8x+490
ges: f(6)
Beispielrechnung: a)·Bourg-d’Oisans·nach·Pied·de·côte:
Höhenunterschied y = 740m – 720m = 20m;
Horizontalunterschied x = 1,5km = 1500m;
also ist m = =0,013 = 1,3%