Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Quadratische Funktionen

Einleitung

In diesem Kapitel geht es darum, Themen aus dem Bereich Quadratische Funktionen zu wiederholen und zu vertiefen.

Dabei schaust du dir an, welchen Einfluss die Parameter auf den Graphen der Funktion haben und machst dich mit Graphen und darauf liegenden Punkten vertraut. Weiter wiederholst du Scheitelpunkt und Nullstellen. Du übst dich im Umgang mit der Normal- und Scheitelpunktform. Anschließend prüfst du deine Kenntnisse an Anwendungsaufgaben. Zu guter letzt kannst du dein Wissen noch in einem finalen Quiz unter Beweis stellen.

In Aufgaben, die gelb gefärbt sind, kannst du Gelerntes wiederholen und vertiefen.

Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.

Und Aufgaben mit grüner Hinterlegung sind Knobelaufgaben.

Scheitelpunktform

1. Parameter der Scheitelpunktform

Fülle den folgenden Lückentext aus. Klicke hierfür auf die Lücke, die du bearbeiten möchtest und wähle die passende Antwort aus. Du kannst deine Antworten überprüfen, indem du unten rechts auf das blaue Symbol klickst. Wenn der Lückentest richtig ausgefüllt ist, kann er dir bei nachfolgenden Aufgaben helfen.

Tipp

Die Scheitelpunktform hat die Funktionsgleichung $g(x)=a\cdot(x-d)^2+e$. Probiere aus was passiert, wenn du die Parameter $a, d$ und $e$ veränderst. Beobachte die Funktionsgleichung und den zugehörigen Graphen.

2.1. Welcher Graph gehört zu welcher Funktionsgleichung?

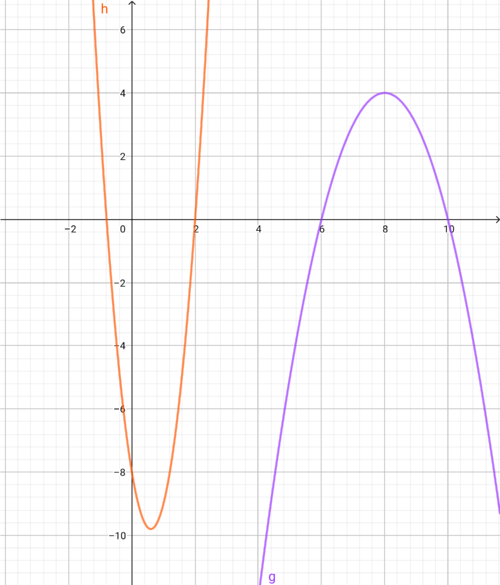
Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Indem du auf die Bilder der Graphen klickst, kannst du sie vergrößern. Außerdem kannst du Paare durch erneutes anklicken auch wieder voneinander trennen.

Tipp 1

Erinnere dich an die Scheitelpunktform und überlege dir, was die Funktionsgleichung mit ihren Parametern über den Graphen verrät. Hierfür lohnt es sich nochmals in die Aufgabe 1 zu schauen.

Tipp 2

Ein Beispiel: Sei die Funktion $f(x)=2(x+8)^2-10$ gegeben. Dann liegt der Scheitelpunkt bei $S(8|10)$. Der Parameter a ist gleich 2. Falls du hierbei noch Schwierigkeiten hast, kannst du dies in Aufgabe 1 nochmal nachlesen.

Tipp 2

Ein Beispiel: Sei die Funktion $f(x)=2(x-8)^2+10$ gegeben. Dann liegt der Scheitelpunkt bei $S(8|10)$. Der Parameter a ist gleich 2. Falls du hierbei noch Schwierigkeiten hast, kannst du dies in Aufgabe 1 nochmal nachlesen.

2.2. Welcher Graph gehört zu welcher Funktionsgleichung?

Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Indem du auf die Bilder der Graphen klickst, kannst du sie vergrößern. Außerdem kannst du Paare durch erneutes Anklicken auch wieder voneinander trennen. Es werden drei Karten übrig bleiben.

Tipp 1

Erinnere dich an die Scheitelpunktform und überlege dir, was die Funktionsgleichung mit ihren Parametern über den Graphen verrät. Hierfür lohnt es sich nochmals in die Aufgabe 1 zu schauen.

Tipp 2

Ein Beispiel: Sei die Funktion $f(x)=2(x+8)^2-10$ gegeben. Dann liegt der Scheitelpunkt bei $S(-8|-10)$. Der Parameter a ist gleich 2. Falls du hierbei noch Schwierigkeiten hast, kannst du dies in Aufgabe 1 nochmal nachlesen.

3. Punkte auf Funktionen

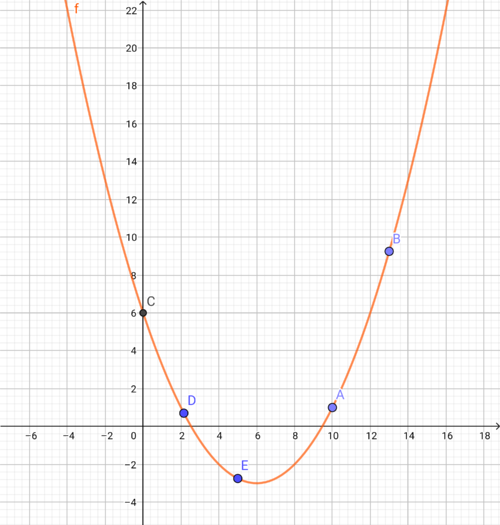
Gegeben sei die Funktion $f(x) =\frac {1} {4} \cdot (x-6)^2-3$ und die Punkte $A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?)$ und $E=(5|?)$

a) Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen.

Tipp 1

Was bedeuten die Variable $x$ und $f(x)$? Wofür sind sie Platzhalter?

Tipp 2

Wenn du die x-Koordinate eines Punktes in eine Funktion einsetzt, berechnest du so seine y-Koordinate.

Lösung zu

Die Punkte besitzen, um auf der Funktion $f(x)$ zu liegen, folgende Koordinaten:
$A=(10|1),, B=(13|\frac {29} {4}) , C=(0|5), D=(\frac{43} {20}|\frac{7}{10})$ und $E=(5|-\frac{11} {4})$

Falls du dir nicht sicher bist, wie man auf die Lösung kommt, findest du hier eine beispielhafte Lösung der Koordinatenberechnung von Punkt A: 1. Da die x-Koordinate des Punktes gegeben ist, setzt man die x-Koordinate für x in die Funktion ein. Man erhält dann:
$f(5) =\frac {1} {4} \cdot (10-6)^2-3$
2. Jetzt muss man den Term noch ausrechnen:
$\frac {1} {4} \cdot (10-6)^2-3$
$= \frac {1} {4} \cdot (4)^2-3$
$= 4-3$

$= 1$

b) Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft.

Tipp 1

Du weißt nicht, wie Du mit Deiner Zeichnung anfangen sollst? Dann schau doch noch einmal in den Lückentext von Aufgabe 1.

Tipp 2

Welcher Punkt ist in einer Funktion der Form $g(x)=a\cdot(x-d)^2+e$ als erstes ablesbar? Beginne deine Zeichnung mit diesem Punkt.

Tipp 3

In einer Funktionsgleichung der Form $g(x)=a\cdot(x-d)^2+e$ gibt dir der Parameter $a$, wie viele Einheiten sich der Graph nach oben oder unten bewegen muss, wenn er sich um eine Einheit nach rechts bewegt.

Lösung zu

Wenn deine Zeichnung wie folgt aussieht, hast du alles richtig gemacht:

Umwandlung Scheitelpunktform und Normalform

Bisher hast du dich intensiv mit der Scheitelpunktform beschäftigt. Quadratische Funktionen können jedoch auch in der Normalform geschrieben werden. In diesem Abschnitt kannst du dein bisheriges Wissen über die Umwandlung von einer Form in die andere Form wiederholen, auffrischen und üben.

4. Die Umwandlungen zwischen Scheitelpunktform und Normalform

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst. Wenn dieser Lückentext richtig ausgefüllt ist, kann er dir bei den nachfolgenden Aufgaben oftmals weiterhelfen. Hinweis: Mit dem Symbol rechts oben kannst du den Lückentext in Vollbildmodus bearbeiten. Mit dem blauen Button rechts unten kannst du deine Eingaben überprüfen.

5. Scheitelpunktform zu Normalform. Finde die Paare!

Wandle die Funktionen f und g in deinem Heft in die Normalform um. Ordne anschließend die gleichen Funktionen einander zu. Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig.

Tipp

Wenn du dir nicht mehr genau weißt, wie du Funktionen von der Scheitelpunktform in die Normalform umschreibst, dann schau dir nochmal die Aufgabe 6 an.

Lösung

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} f(x) &=& (x+3)^2+4 &\mid \, 1. \, Binomische \, Formel \\ &=& (x^2+6x+9)+4 &\mid \, zusammenfassen \\ &=& x^2 +6x +13 \end{array}$

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} g(x) &=& 2 \cdot (x-3)^2+9 &\mid \, 2. \, Binomische \, Formel \\ &=& 2 \cdot (x^2 -6x +9)+9 &\mid \, ausmultiplizieren \\ &=& 2x^2-12x+18+9 &\mid zusammenfassen \\ &=& 2x^2-12x+27 \end{array}$

6. Normalform zu Scheitelpunktform. Finde die Paare!

Wandle die Funktionen f und g in deinem Heft in die Scheitelpunktform um. Ordne anschließend die gleichen Funktionen einander zu. Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig.

Tipp

Wenn du dir nicht mehr genau weißt, wie du von Funktionen von der Normalform in die Scheitelpunktform umschreibst, dann schau dir nochmal die Aufgabe 6 an.

Lösung

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} f(x) &=& x^2-14x-4 &\mid \, quadratische \, Erg\ddot{a}nzung \\ &=& x^2-14x +7^2-7^2-4 &\mid \, 2. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& (x-7)^2-7^2-4 &\mid \, zusammenfassen \\ &=& (x-7)^2 -53 \end{array}$

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} g(x) &=& -2 \cdot x^2 -12x -11 &\mid \, (-2) \, ausklammern \\ &=& -2 \cdot [x^2+6x+\frac{11}{2}] &\mid \, quadratische\, Erg\ddot{a}nzung \\ &=& -2 \cdot [x^2+6x+3^2-3^2+\frac{11}{2}] &\mid \, 1. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& -2 \cdot [(x+3)^2-9+\frac{11}{2}] &\mid \, zusammenfassen \\ &=& -2 \cdot [(x+3)^2-\frac{7}{2}] &\mid \, ausmultiplizieren \\ &=& -2 \cdot (x+3)^2 +7 \end{array}$

Nullstellen

7. Berechnung von Nullstellen

Gegeben seien folgende Funktionen:
$g(x) = - 1 \cdot (x-8)^2+4$
$h(x) = 5x^2-6x-8$
Berechne von beiden Funktionen jeweils die Nullstellen.
Du kannst als Hilfe Zettel und Stift verwenden.

Tipp 1

Denke über die Bedeutung einer Nullstelle nach. Was bedeutet es, wenn eine Funktion an einem Punkt eine Nullstelle besitzt?

Tipp 2

Ein Punkt wird als Nullstelle einer Funktion bezeichnet, wenn seine y-Koordinate gleich 0 ist.
D.h. um die Nullstellen einer Funktion zu bestimmen, solltest du die Funktion gleich 0 setzen.
Für die nächsten Schritte gibt es verschiedene Möglichkeiten vorzugehen: Ist deine Funktion in Scheitelpunktform, so hilft es dir den Term $(x-d) ^2$ auf einer Seite zu isolieren, um dann die Wurzel ziehen zu können.

Ansonsten gibt es als Hilfsmittel noch die dir bereits bekannte pq-Formel oder quadratische Ergänzung.

Tipp 3

pq-Formel

Eine Funktion der Form $f(x)=x^2+px+q$ hat die Lösungen $x_{1} = -\frac{p}{2}-\sqrt{\left( \frac{p}{2}\right)^2-q}$ sowie $x_{2} = -\frac{p}{2}+\sqrt{\left( \frac{p}{2}\right)^2-q}$. Dieses Hilfsmittel hilft dir bei der Berechnung der Nullstellen von $f(x)$.

Lösungen

$g(x)$ liegt in Scheitelpunktform vor, weswegen eine Möglichkeit die Nullstellen zu bestimmen Folgende ist:

$\begin{array}{rlll} && g(x) &&=&& 0 \\ &\Leftrightarrow& 0 &&=&& -1(x-8)^2+4 &\mid :(-1) \\ &\Leftrightarrow& 0 &&=&& (x-8)^2-4 &\mid +4 \\ &\Leftrightarrow& 4 &&=&& (x-8)^2 & \mid \pm\sqrt{} \\ \end{array}$

$\begin{array}{rlll} &\Rightarrow&(x_1-8) = 2& \textrm{sowie}& (x_2-8)=-2\\ \end{array}$

Lösung zu h(x)

$h(x)$ liegt in Normalform vor. Es empfiehlt sich also die Funktion so umzuformen,so dass man die pq-Formel anwenden kann.

Betrachte $h(x)=0$, d.h. $0 = 5x^2-6x-8$ und führe dann eine Äquivalenzumformung durch, indem du durch 5 teilst.

Du erhälst die Gleichung $0 = x^2-\frac {6} {5} x-\frac{8}{5}$

Durch Anwenden der pq-Formel folgt

$\begin{array} {rlll} &\Rightarrow&x_{1} = -\frac{-\frac{6}{5}}{2}-\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}& \textrm{sowie}& x_{2} = -\frac{-\frac{6}{5}}{2}+\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}\\ &\Rightarrow&x_1 = 0,8& \textrm{und}& x_2 = 2\\ \end{array}$

Darstellung der Graphen

Anwendungsaufgaben

8. Frösche sind wahre Sprungkünstler

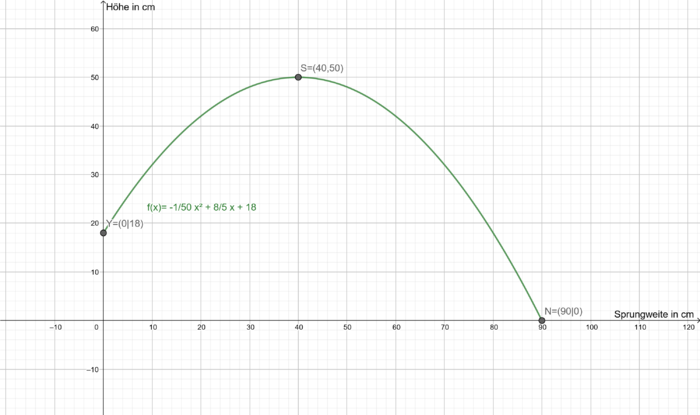
Das Geheimnis der bemerkenswerten Sprungkraft von Fröschen liegt in den Sehnen ihrer Hinterbeine, die zunächst durch Muskelkraft gespannt werden und den Frosch dann explosiv vorwärts katapultieren können. Frösche können damit ein Vielfaches ihrer Körpergröße weit springen. So kann der Grasfrosch beispielsweise bis zu 1 Meter weit springen. In den Rieselfeldern in Münster wurde vor ein paar Tagen der Sprung eines solchen Grasfrosches beobachtet. Er ist von einem 18cm hohen Stein am Ufer eines Teichs ins Wasser gesprungen. Die Flugbahn des Frosches lässt sich näherungsweise durch folgende quadratische Funktion beschreiben:$f(x)=-\frac{1}{50}x^2+\frac{8}{5}x+18,$ wobei $x$ die Entfernung des Frosches vom Ufer des Teichs und $f(x)$ die Höhe des Frosches (jeweils in cm) beschreibt.

a) Wie hoch springt der Frosch? Und nach wie vielen Zentimetern erreicht der Frosch seinen höchsten Punkt?

Tipp 1

Du möchtest den Punkt berechnen, an dem der Frosch am höchsten ist. Die angegebene Funktion beschreibt eine nach unten geöffnete Parabel. Überlege dir, wo sich der höchste Punkt einer solchen Parabel befindet und wie man ihn berechnet.

Tipp 2

Der Frosch erreicht seinen höchsten Punkt am Scheitelpunkt der Funktion. Um den Scheitelpunkt einer quadratischen Funktion ablesen zu können, musst du diese in Scheitelpunktform bringen. Du hast Probleme, die Funktion in Scheitelpunktform umzuwandeln? Aufgabe 4 zeigt dir genau, wie es funktioniert.

Lösung

1) Umwandlung in Scheitelpunktform

$\begin{array}{rlll} f(x) &=& -\frac{1}{50}x^2+\frac{8}{5}x+18 &\mid -\frac{1}{50} \, \text{ausklammern} \\ &=& -\frac{1}{50}(x^2-80x-900) &\mid \, \text{quadratische} \, \text{Ergänzung} \\ &=& -\frac{1}{50}(x^2-80x+1600-1600-900) &\mid \, \text{binomische} \, \text{Formel} \, \text{anwenden} \, \text{und} \, \text{zusammenfassen} \\ &=& -\frac{1}{50}[(x-40)^2-2500] &\mid \, \text{ausmultiplizieren} \\ &=& -\frac{1}{50}(x-40)^2+50 \end{array}$

2) Scheitelpunkt ablesen

Der Scheitelpunkt der Funktion ist $S=(40|50)$.

3) Interpretieren im Anwendungskontext

Nach $40cm$ erreicht der Frosch seinen höchsten Punkt. Er befindet sich dann $50cm$ über der Wasseroberfläche. Da der Frosch vor seinem Sprung auf einem $18cm$ hohen Stein saß, ist er folglich $32cm$ hoch gesprungen.

b) In welcher Entfernung vom Ufer des Teichs taucht der Frosch ins Wasser ein?

Tipp 1 zu Aufgabenteil b)

Überlege dir auf welcher Höhe der Frosch ins Wasser taucht.

Tipp 2 zu Aufgabenteil b)

Bei diesem Aufgabenteil werden die Nullstellen der Funktion gesucht. An einer dieser Nullstellen taucht der Frosch nämlich ins Wasser ein. Überlege dir, welche Nullstelle im Anwendungskontext Sinn ergibt. Falls du Probleme hast, die Nullstellen einer quadratischen Funktion zu bestimmen, sieh dir Aufgabe 6 an.

Lösung zu Aufgabenteil b)

1) Nullstellen berechnen durch quadratische Ergänzung

$\begin{array}{rlll} && f(x) &&=&& 0 \\ &\Leftrightarrow& -\frac{1}{50}\cdot(x-40)^2+50 &&=&& 0 &\mid \cdot(-50)\\ &\Leftrightarrow& (x-40)^2-2500 &&=&& 0 &\mid +2500 \\ &\Leftrightarrow& (x-40)^2 &&=&& 2500 &\mid \pm\sqrt{} \\ \end{array}$

$\begin{array}{rlll} &\Rightarrow&(x_1-40)=50& \textrm{sowie}& (x_2-40)=-50\\ \end{array}$

Also folgt $x_1=90$ und $x_2=-10$.

2) Nullstellen berechnen mit der p-q-Formel

$\begin{array}{rlll} && f(x) &&=&& 0 \\ &\Leftrightarrow& -\frac{1}{50}x^2+\frac{8}{5}x+18 &&=&& 0 &\mid \cdot(-50)\\ &\Leftrightarrow& x^2-80x-900 &&=&& 0 &\mid +2500 \\ \end{array}$

$\begin{array}{rlll} &\Rightarrow&x_1=40+\sqrt{40^2+900}& \textrm{sowie}& x_2=40-\sqrt{2500}\\ &\Rightarrow&x_1=90& \textrm{sowie}& x_2=-10\\ \end{array}$

Also folgt $x_1=90$ und $x_2=-10$.

Damit hat die Funktion also zwei Nullstellen. Da wir jedoch davon ausgehen, dass der Frosch nach vorne in den Teich springt, beträgt die Sprungweite $90cm$.

c) Zeichne die Flugbahn des Frosches in dein Heft.

Tipp 1 zu Aufgabenteil c)

Kennst du nicht bereits Punkte, die auf dem Graphen der Funktion liegen? Überlege dir, welche Punkte du bereits berechnet hast und welche du aus den beiden Darstellungsformen der Funktion (Normalform und Scheitelpunktform) ablesen kannst.

Tipp 2 zu Aufgabenteil c)

Zeichne zunächst den Scheitelpunkt $S=(d|e)$, den y-Achsenabschnitt $Y=(0|c)$ und die Nullstelle $N=(x_1|0)$ ein.

Lege danach eine Wertetabelle an und berechne weitere Punkte des Funktionsgraphen.

Lösung zu Aufgabenteil c)

Beachte, dass die Flugbahn erst mit dem Absprung des Frosches beginnt und mit dem Auftreffen des Frosches auf der Wasseroberfläche endet.

Auf der x-Achse trägst du die Sprungweite des Frosches in Zentimetern ab, auf der y-Achse die Höhe des Frosches in Zentimetern.

9. Hochsprung

In der Leichtathletik nennt man die momentan praktizierte Technik beim Hochsprung den sogenannten Fosbury-Flop. Der Springer schwingt sich hierbei rückwärts über die Latte. Dabei beschreibt die Flugbahn des Körperschwerpunktes eine Parabel. Wenn man aufrecht steht liegt der Körperschwerpunkt bei etwa 60% der Körpergröße. Bei der letzten Leichtathletik-Weltmeisterschaft in Doha diesen Jahres konnten bei einem Sprung eines männlich Sportlers (ca. 1,92cm groß) folgende Werte seiner Flugbahn aufgezeichnet werden: $D=(0|1.15), \, E=(0.2|1.5), \, F=(1.2|1.75)$. Dabei beschreibt der x-Wert die Entfernung des Springers vom Absprungsort und der y-Wert die Höhe des Springers (jeweils in Meter).

a) Bestimme die dazugehörige Flugparabel $g(x)=ax^2+bx+c$.

Tipp 1 zu Aufgabenteil a)

Überlege dir, was du benötigst, um eine quadratische Funktion aufstellen zu können.

Tipp 2 zu Aufgabenteil a)

Stelle mithilfe der angegebenen Punkte drei quadratische Gleichungen ($ax^2+bx+c=d$) auf, indem du die Punkte in die allgemeine Form einsetzt! Welche von den Variablen $a, b, c$ kannst du bereits ablesen? Und wie könntest du die anderen beiden Variablen berechnen?

Lösung zu Aufgabenteil a)

1) Lineares Gleichungssystem aufstellen

$\begin{array}{rlll} &&I. &a\cdot0^2&+&b\cdot0&+&c &=& 1.15 \\ && II. &a\cdot0.2^2&+&b\cdot0.2&+&c &=& 1.5 \\ &&III. &a\cdot1.2^2&+&b\cdot1.2&+&c &=& 1.75 \\ && \\ &&I. &&&&&c &=& 1.15 \\ &&II. &0.04a&+&0.2b&+&1.15 &=& 1.5 \\ &&III. &1.44a&+&1.2b&+&1.15 &=& 1.75 \\ \end{array}$

2) Zweite Gleichung nach $a$ auflösen

$\begin{array}{rlll} && 0.04a+0.2b+1.15 &=& 1.5 &\mid -1.15 \\ &\Leftrightarrow& 0.04a+0.2b &=& 0.35 &\mid -0.2b \\ &\Leftrightarrow& 0.04a &=& 0.35-0.2b &\mid :0.04 \\ &\Leftrightarrow& a &=& \frac{0.35}{0.04}-\frac{0.2b}{0.04} \\ &\Leftrightarrow& a &=& 8.75-5b \end{array}$

3) $a=8.75-5b$ in die dritte Gleichung einsetzen und nach $b$ auflösen

$\begin{array}{rlll} && 1.44(8.75-5b)+1.2b+1.15 &=& 1.75 &\mid \, \text{ausmultiplizieren} \, \text{und} \, \text{zusammenfassen} \\ &\Leftrightarrow& -6b+13.75 &=& 1.75 &\mid \, -13.75 \\ &\Leftrightarrow& -6b &=& -12 &\mid \, :(-6) \\ &\Leftrightarrow& b &=& 2 \\ \end{array}$

4) $b=2$ in die Gleichung $a=8.75-5b$ einsetzen

$\begin{array}{rlll} &\Rightarrow& a=-1.25 \\ \end{array}$

5) Quadratische Funktion $g(x)=ax^2+bx+c$ aufstellen

$\begin{array}{rlll} &\Rightarrow& g(x)=-1.25x^2+2x+1.15 \\ \end{array}$

b) Wie hoch springt der Sportler? Und in welcher Entfernung vom Absprungspunkt erreicht er seinen höchsten Punkt?

Tipp 1 zu Aufgabenteil b)

Du möchtest den Punkt berechnen, an dem der Körperschwerpunkt des Sportlers am höchsten ist. Die angegebene Funktion beschreibt eine nach unten geöffnete Parabel. Überlege dir, wo sich der höchste Punkt einer solchen Parabel befindet und wie man ihn berechnet.

Tipp 2 zu Aufgabenteil b)

Der Körperschwerpunkt des Sportlers erreicht seinen höchsten Punkt am Scheitelpunkt der Funktion. Um den Scheitelpunkt einer quadratischen Funktion ablesen zu können, musst du diese in Scheitelpunktform bringen. Du hast Probleme, die Funktion in Scheitelpunktform umzuwandeln? Aufgabe … zeigt dir genau, wie es funktioniert.

Lösung zu Aufgabenteil b)

1) Umwandlung in Scheitelpunktform

$\begin{array}{rlll} g(x) &=& -1.25x^2+2x+1.15 &\mid -1.25 \, \text{ausklammern} \\ &=& -1.25(x^2-1.6x-0.92) &\mid \, \text{quadratische} \, \text{Ergänzung} \\ &=& -1.25(x^2-1.6x+0.64-0.64-0.92) &\mid \, \text{binomische} \, \text{Formel} \, \text{anwenden} \, \text{und} \, \text{zusammenfassen} \\ &=& -1.25[(x-0.8)^2-1.56] &\mid \, \text{ausmultiplizieren} \\ &=& -1.25(x-0.8)^2+1.95 \\ \end{array}$

2) Scheitelpunkt ablesen

Der Scheitelpunkt der Funktion ist $S=(0.8|1.95)$.

3) Interpretieren im Anwendungskontext

Nach $0.8m$ erreicht der Sportler seinen höchsten Punkt. Er befindet sich dann auf einer Höhe von $1.95m$.

c) Hinter der Latte befindet sich eine $15cm$ hohe Matte. In welcher Entfernung zum Absprungsort landet der Sportler auf der Matte?

Tipp 1 für Aufgabenteil c)

Überlege dir an welcher Stelle du die $15cm$ in deine Funktionsgleichung einsetzen musst. Und welche Variable musst du jetzt noch berechnen?

Tipp 2 zu Aufgabenteil c)

Die $15cm$ beschreiben einen Funktionswert, also $g(x)=0.15$. Um herauszufinden, an welchem Punkt der Sportler auf der Matte landet, musst du die Gleichung nun nach $x$ auflösen.

Lösung zu Aufgabenteil c)

1) Quadratische Funktion mit $y=0.15$ gleichsetzen und nach $x$ auflösen

$\begin{array}{rlll} && g(x) &=& 0.15 \\ &\Leftrightarrow& -1.25(x-0.8)^2+1.95 &=& 0.15 &\mid \, -1.95 \\ &\Leftrightarrow& -1.25(x-0.8)^2 &=& -1.8 &\mid \, :(-1.25) \\ &\Leftrightarrow& (x-0.8)^2 &=& 1.44 &\mid \, \pm\sqrt{} \\ \end{array}$

$\begin{array}{rlll} &\Rightarrow&(x_1-0.8)=1.2& \textrm{sowie}& (x_2-0.8)=-1.2\\ \end{array}$

Also folgt $x_1=2$ und $x_2=-0.4$.

2) Interpretieren im Anwendungskontext

Da wir davon ausgehen können, dass der Sportler nach vorne springt, ergibt nur $x_1=2$ Sinn. Der Sportler landet also in einer Entfernung von $2m$ zum Absprungspunkt auf der Matte.

d) Bei einem optimalen Sprung liegt der Scheitelpunkt genau über der Latte. Der Abstand zur Latte muss mindestens $5cm$ betragen, damit diese nicht gerissen wird. Wir gehen davon aus, dass unser Sportler einen optimalen Sprung getätigt hat, d.h. die Latte war $0.8m$ vom Absprungsort entfernt und hatte eine Höhe von $1.88m$. Hätte der Sportler es auch noch über die Latte geschafft, ohne sie zu reißen, wenn er $0.2m$ früher abgesprungen wäre?

Tipp 1 zu Aufgabenteil d)

Überlege dir, was die $0.2m$ für den von dir aufgestellten Funktionsterm bedeuten. Musst du jetzt nochmal einen neuen Funktionsterm aufstellen oder kannst du deinen alten vielleicht geschickt anpassen?

Tipp 2 zu Aufgabenteil d)

Du willst den Funktionsgraphen deines Funktionsterms entlang der x-Achse um $0.2$ nach links verschieben. Was musst du hierfür tun?

Lösung zu Aufgabenteil d)

1) Verschiebung der quadratischen Funktion an der x-Achse um $0.2$ nach links

$\begin{array}{rlll} &\Rightarrow& g(x)=-1.25(x+0.2)^2+2(x+0.2)+1.15 \\ \end{array}$

2) Für $x$ den Wert $0.8$ einsetzen

$\begin{array}{rlll} g(0.8) &=& -1.25(0.8+0.2)^2+2(0.8+0.2)+1.15 &\mid \, \text{ausmultiplizieren} \, \text{und} \, \text{zusammenfassen} \\ &=& 1.9 \\ \end{array}$

3) Interpretieren im Anwendungskontext

Wenn der Sportler $0.2m$ früher abgesprungen wäre, hätte er bloß einen Abstand von $2cm$ zur Latte gehabt und hätte sie damit gerissen.

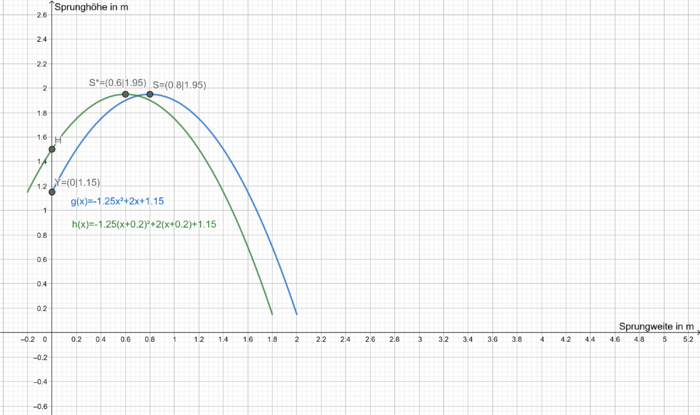
e) Zeichne beide Flugbahnen des Sportlers in dein Heft.

Tipp 1 zu Aufgabenteil e)

Kennst du nicht bereits Punkte, die auf dem Graphen der ursprünglichen Funktion liegen? Überlege dir, welche Punkte du bereits berechnet hast und welche du aus den beiden Darstellungsformen der Funktion (Normalform und Scheitelpunktform) ablesen kannst.

Tipp 2 zu Aufgabenteil e)

Zeichne zunächst den Scheitelpunkt $S=(d|e)$, den y-Achsenabschnitt $Y=(0|c)$ und den Schnittpunkt mit der Matte $N=(x_1|0.15)$ der ersten Funktion ein.

Lege danach eine Wertetabelle an und berechne weitere Punkte des Funktionsgraphen.

Tipp 3 zu Aufgabeteil e)

Überlege dir was sich bei der zweiten Flugbahn verändert hat und was das für die zwei Funktionsgraphen bedeutet.

Lösung zu Aufgabenteil e)

Beachte, dass die Flugbahn erst mit dem Absprung des Sportlers beginnt und mit dem Auftreffen des Sportlers auf der Matte endet. Auf der x-Achse trägst du die Sprungweite des Sportlers in Metern ab, auf der y-Achse die Höhe des Sportlers in Metern.

Der zweite Funktionsgraph ist lediglich um 0.2 nach links verschoben. Ansonsten stimmt er komplett mit dem ersten Funktionsgraphen überein.

 

10. Das Quiz

Schaffst du es abschließend durch alle Fragen?