Digitale Werkzeuge in der Schule/Wie Funktionen funktionieren 2.0/Quadratische Funktionen

Einleitung

In diesem Kapitel geht es darum, Themen aus dem Bereich "Quadratische Funktionen" zu wiederholen und zu vertiefen.

Dabei schaust du dir an, welchen Einfluss die Parameter auf das "Aussehen" des Graphen der Funktion haben und machst dich mit Graph und darauf liegenden Punkten vertraut. Weiter wiederholst du die besonders wichtigen Punkte: Scheitelpunkt und Nullstellen und übst den Umgang mit der Normal- und Scheitelpunktsform. Anschließend prüfst du deine Kenntnisse an einer Anwendungsaufgabe. Zu guter letzt kannst du dein Wissen noch in einem finalen Quiz unter Beweis stellen.

Du wirst in diesem Lernpfad unterschiedliche Schwierigkeitsgrade auffinden. Siehst du eine gelbe Aufgabe vor dir, so handelt es sich um die Schwierigkeitsstufe 1, blau entspricht der Schwierigkeitsstufe 2 und grün entspricht der Schwierigkeitsstufe 3.

Scheitelpunktform

1. Parameter der Scheitelpunktform

Fülle den folgenden Lückentext aus. Klicke hierfür auf die Lücke, die du bearbeiten möchtest und wähle die passende Antwort aus. Du kannst deine Antworten überprüfen, indem du unten rechts auf das blaue Symbol klickst. Wenn der Lückentest richtig ausgefüllt ist, kann er dir bei nachfolgenden Aufgaben helfen.

Die Scheitelpunktform hat die Funktionsgleichung $g(x)=a\cdot(x-d)^2+e$. Probiere aus was passiert, wenn du die Parameter $a, d$ und $e$ veränderst. Beobachte die Funktionsgleichung und den zugehörigen Graphen.

2. Welcher Graph gehört zu welcher Funktionsgleichung?

Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Indem du auf die Bilder der Graphen klickst, kannst du sie vergrößern. Außerdem kannst du Paare durch erneutes anklicken auch wieder voneinander trennen.

Erinnere dich an die Scheitelpunktform und überlege dir, was die Funktionsgleichung mit ihren Parametern über den Graphen verrät. Hierfür lohnt es sich nochmals in die Aufgabe 1 zu schauen.

Sei die Funktion $f(x)=2(x-8)^2+10$ gegeben. Dann liegt der Scheitelpunkt bei (8/10). Falls du hierbei noch Schwierigkeiten hast, kannst du dies in Aufgabe 1 nochmal nachlesen. Der Parameter a ist gleich 2. Wenn du eine Einheit vom Scheitelpunkt nach rechts/links gehst, gehst du zwei Einheiten nach oben und gelangst an einen weiteren Punkt auf deinem Graphen.

2.1. Welcher Graph gehört zu welcher Funktionsgleichung?

Ordne die folgenden Funktionsgleichungen den zugehörigen Graphen zu. Hinweis: Indem du auf die Bilder der Graphen klickst, kannst du sie vergrößern. Außerdem kannst du Paare durch erneutes anklicken auch wieder voneinander trennen. Dieses Mal werden drei Felder übrig bleiben.

Erinnere dich an die Scheitelpunktform und überlege dir, was die Funktionsgleichung mit ihren Parametern über den Graphen verrät. Hierfür lohnt es sich nochmals in die Aufgabe 1 zu schauen.

Sei die Funktion $f(x)=-2(x+8)^2-10$ gegeben. Dann liegt der Scheitelpunkt bei (-8/-10). Falls du hierbei noch Schwierigkeiten hast, kannst du dies in Aufgabe 1 nochmal nachlesen. Der Parameter a ist gleich -2. D.h. wenn du eine Einheit vom Scheitelpunkt nach rechts/links gehst, gehst du zwei Einheiten nach unten und gelangst an einen weiteren Punkt auf deinem Graphen.

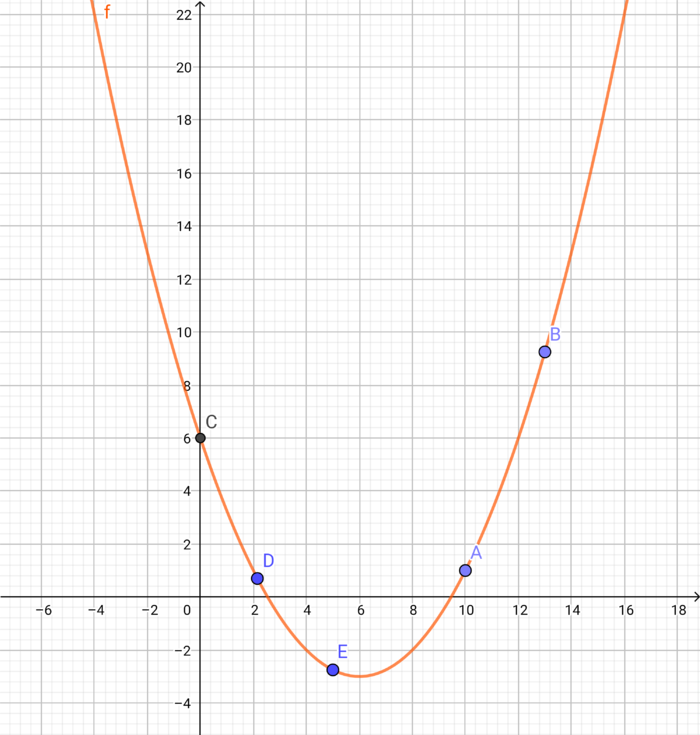
3. Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen.

Gegeben sei die Funktion $f(x) =\frac {1} {4} \cdot (x-6)^2-3$ und die Punkte $A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?)$ und $E=(5|?)$

a) Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen.

Was bedeuten die Variable $x$ und $f(x)$? Wofür sind sie Platzhalter?

Wenn du die x-Koordinate eines Punktes in eine Funktion einsetzt, berechnest du so seine y-Koordinate.

Die Punkte besitzen, um auf der Funktion $f(x)$ zu liegen, folgende Koordinaten:

$A=(10|1),, B=(13|\frac {29} {4}) , C=(0|5), D=(\frac{43} {20}|\frac{7}{10})$ und $E=(5|-\frac{11} {4})$

b) Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft.

Du weißt nicht, wie Du mit Deiner Zeichnung anfangen sollst? Dann schau doch noch einmal in den Lückentext von Aufgabe 1.

Welcher Punkt ist in einer Funktion der Form $g(x)=a\cdot(x-d)^2+e$ als erstes ablesbar? Beginne deine Zeichnung mit diesem Punkt.

In einer Funktionsgleichung der Form $g(x)=a\cdot(x-d)^2+e$ gibt dir der Parameter $a$, wie viele Einheiten sich der Graph nach oben oder unten bewegen muss, wenn er sich um eine Einheit nach rechts bewegt.

Wenn deine Zeichnung wie folgt aussieht, hast du alles richtig gemacht:

Umwandlung Scheitelpunktform und Normalform

Bisher hast du dich intensiv mit der Scheitelpunktform beschäftigt. Quadratische Funktionen können jedoch auch in der Normalform geschrieben werden. In diesem Abschnitt kannst du dein bisheriges Wissen über die Umwandlung von einer Form in die andere Form wiederholen, auffrischen und üben.

4. Die Umwandlungen zwischen Scheitelpunktform und Normalform

Fülle den Lückentext aus, indem du auf eine Lücke klickst und die richtige Antwort auswählst. Wenn dieser Lückentext richtig ausgefüllt ist, kann er dir bei den nachfolgenden Aufgaben oftmals weiterhelfen. Hinweis: Mit dem Symbol rechts oben kannst du den Lückentext in Vollbildmodus bearbeiten. Mit dem blauen Button rechts unten kannst du deine Eingaben überprüfen.

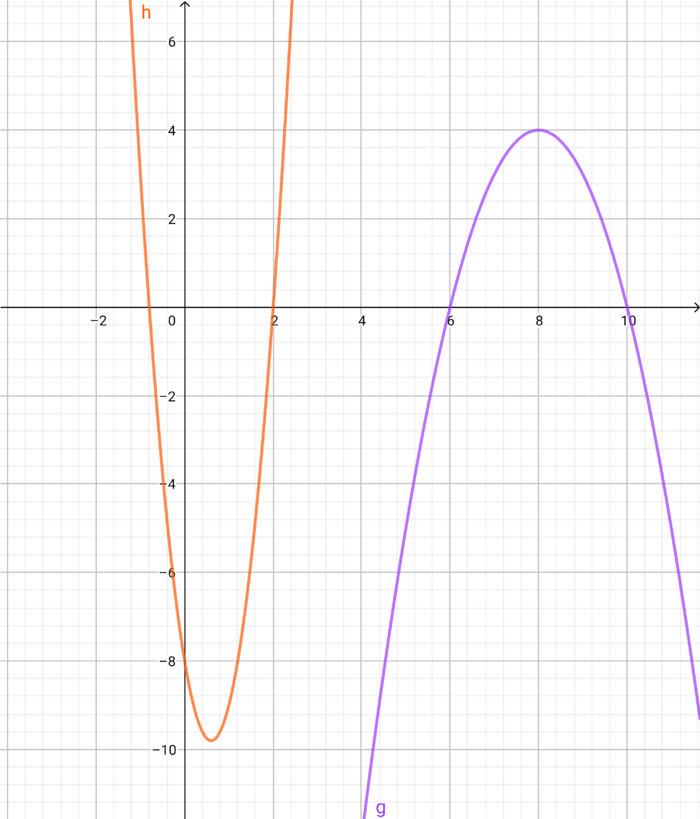
5. Scheitelpunktform zu Normalform. Finde die Paare!

Wandle die Funktionen f und g in deinem Heft in die Normalform um. Ordne anschließend die gleichen Funktionen einander zu. Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig.

Wenn du dir nicht mehr genau weißt, wie du Funktionen von der Scheitelpunktform in die Normalform umschreibst, dann schau dir nochmal die Aufgabe 6 an.

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} f(x) &=& (x+3)^2+4 &\mid \, 1. \, Binomische \, Formel \\ &=& (x^2+6x+9)+4 &\mid \, zusammenfassen \\ &=& x^2 +6x +13 \end{array}$

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} g(x) &=& 2 \cdot (x-3)^2+9 &\mid \, 2. \, Binomische \, Formel \\ &=& 2 \cdot (x^2 -6x +9)+9 &\mid \, ausmultiplizieren \\ &=& 2x^2-12x+18+9 &\mid zusammenfassen \\ &=& 2x^2-12x+27 \end{array}$

6. Normalform zu Scheitelpunktform. Finde die Paare!

Wandle die Funktionen f und g in deinem Heft in die Scheitelpunktform um. Ordne anschließend die gleichen Funktionen einander zu. Hinweis: Es bleiben am Ende drei Funktionsgleichungen übrig.

Wenn du dir nicht mehr genau weißt, wie du von Funktionen von der Normalform in die Scheitelpunktform umschreibst, dann schau dir nochmal die Aufgabe 6 an.

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} f(x) &=& x^2-14x-4 &\mid \, quadratische \, Erg\ddot{a}nzung \\ &=& x^2-14x +7^2-7^2-4 &\mid \, 2. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& (x-7)^2-7^2-4 &\mid \, zusammenfassen \\ &=& (x-7)^2 -53 \end{array}$

[Lösung anzeigen][Lösung ausblenden]

$\begin{array}{rlll} g(x) &=& -2 \cdot x^2 -12x -11 &\mid \, (-2) \, ausklammern \\ &=& -2 \cdot [x^2+6x+\frac{11}{2}] &\mid \, quadratische\, Erg\ddot{a}nzung \\ &=& -2 \cdot [x^2+6x+3^2-3^2+\frac{11}{2}] &\mid \, 1. \, Binomische \, Formel \, r\ddot{u}ckw\ddot{a}rts \, anwenden \\ &=& -2 \cdot [(x+3)^2-9+\frac{11}{2}] &\mid \, zusammenfassen \\ &=& -2 \cdot [(x+3)^2-\frac{7}{2}] &\mid \, ausmultiplizieren \\ &=& -2 \cdot (x+3)^2 +7 \end{array}$

Nullstellen

7. Berechnung von Nullstellen

Gegeben seien folgende Funktionen:
$g(x) = - 1 \cdot (x-8)^2+4$
$h(x) = 5x^2-6x-8$

Berechne von beiden Funktionen jeweils die Nullstellen.

Denke über die Bedeutung einer Nullstelle nach. Was bedeutet es, wenn eine Funktion an einem Punkt eine Nullstelle besitzt?

Ein Punkt wird als Nullstelle einer Funktion bezeichnet, wenn seine y-Koordinate gleich 0 ist.
D.h. um die Nullstellen einer Funktion zu bestimmen, solltest du die Funktion gleich 0 setzen.
Für die nächsten Schritte gibt es verschiedene Möglichkeiten vorzugehen: Ist deine Funktion in Scheitelpunktform, so hilft es dir den Term $(x-d) ^2$ auf einer Seite zu isolieren, um dann die Wurzel ziehen zu können.

Ansonsten gibt es als Hilfsmittel noch die dir bereits bekannte pq-Formel oder quadratische Ergänzung.

pq-Formel

Eine Funktion der Form $f(x)=x^2+px+q$ hat die Lösungen $x_{1} = -\frac{p}{2}-\sqrt{\left( \frac{p}{2}\right)^2-q}$ sowie $x_{2} = -\frac{p}{2}+\sqrt{\left( \frac{p}{2}\right)^2-q}$. Dieses Hilfsmittel hilft dir bei der Berechnung der Nullstellen von $f(x)$.

$g(x)$ liegt in Scheitelpunktform vor, weswegen eine Möglichkeit die Nullstellen zu bestimmen Folgende ist:

$\begin{array}{rlll} && g(x) &&=&& 0 \\ &\Leftrightarrow& 0 &&=&& -1(x-8)^2+4 &\mid :(-1) \\ &\Leftrightarrow& 0 &&=&& (x-8)^2-4 &\mid +4 \\ &\Leftrightarrow& 4 &&=&& (x-8)^2 & \mid \pm\sqrt{} \\ \end{array}$

$\begin{array}{rlll} &\Rightarrow&(x_1-8) = 2& \textrm{sowie}& (x_2-8)=-2\\ \end{array}$

$h(x)$ liegt in Normalform vor. Es empfiehlt sich also die Funktion so umzuformen,so dass man die pq-Formel anwenden kann.

Betrachte $h(x)=0$, d.h. $0 = 5x^2-6x-8$ und führe dann eine Äquivalenzumformung durch, indem du durch 5 teilst.

Du erhälst die Gleichung $0 = x^2-\frac {6} {5} x-\frac{8}{5}$

Durch Anwenden der pq-Formel folgt

$\begin{array} {rlll} &\Rightarrow&x_{1} = -\frac{-\frac{6}{5}}{2}-\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}& \textrm{sowie}& x_{2} = -\frac{-\frac{6}{5}}{2}+\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}\\ &\Rightarrow&x_1 = 0,8& \textrm{und}& x_2 = 2\\ \end{array}$

10. Das Quiz

Schaffst du es abschließend durch alle Fragen? Dann kannst du dir sicher sein das Thema voll und ganz durchschaut zu haben!