Geometrie im Dreieck

Diese Seite ist aktuell im Aufbau.

Info

Willkommen auf dem Online-Lernpfad!

In verschiedenen Kapiteln erkundest du die Eigenschaften von Dreiecken und lernst, wie man diese geschickt zu Aufgabenlösungen verwenden kann.

Hierfür brauchst du dein Wissen über Winkel. Daher geht es los mit einer kurzen Wiederholung.

 

Teste dein Vorwissen

1 Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein

	Die Winkel α und β sind Nebenwinkel.
	Die Winkel α und β sind Scheitelwinkel.
	Die Winkel ε und δ sind Stufenwinkel.
	Die Winkel ζ und δ sind Wechselwinkel.

2 Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein

	Scheitelwinkel sind immer gleich groß.
	Wechselwinkel sind zusammen immer 90 Grad groß.
	Die Winkel α und γ sind zusammen 180 Grad groß.
	Nebenwinkel sind immer zusammen 180 Grad groß.

3 Welche Aussagen stimmen? Es können mehrere Aussagen richtig sein

	Wenn α = 120° ist, dann ist θ = 120°
	Wenn θ = 120° ist, dann ist ε = 60°
	Wenn α = 60° ist, dann ist γ = 120°
	Wenn ζ = 160° ist, dann ist γ = 20°

4 Rechts siehst du ein Dreieck. Welche Größen müssen vorgegeben sein, damit du das Dreieck konstruieren kannst? Es können mehrere Aussagen richtig sein

	Länge b, c und Größe β
	Länge b, c und Größe α
	Länge a, b und Größe γ
	Länge a und Größe β, α
	Länge b und Größe β
	Länge c und Größe α, β
	Man kann nur ein Dreieck konstruieren, wenn man alle sechs Größen kennt

Wie geht es nun weiter?

Wenn du alle Aufgaben richtig beantwortet hast:

• Suche dir aus den in den folgenden Abschnitten genannten Themen eines (oder mehrere) aus. Zu jedem Thema gibt es neben Förder- auch Forderaufgaben, mit denen du dich beschäftigen kannst.

Wenn du einen oder auch mehrere Fehler gemacht hast:

• bei den Aufgaben 1 - 3, gehe zu: Auf den Spuren der Winkel

Zu den Kapiteln

Kapitelübersicht

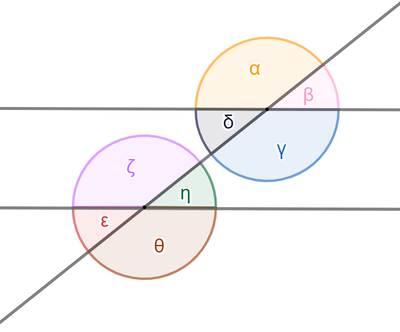
Auf den Spuren der Winkel - Neben-, Scheitel-, Stufen- und Wechselwinkel

Geheimcode der Geometrie - Die Jagd nach der Winkelsumme

Mehr als eine Linie - Mittelsenkrechte, Winkelhalbierende und Seitenhalbierende

Komm zum Punkt - Verschiedene Punkte des Dreiecks

Triangle-Architects - Dreiecke konstruieren