Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Break-Even-Point

zurück zur Seite der Herta-Lebenstein-Realschule

Break-Even-Point

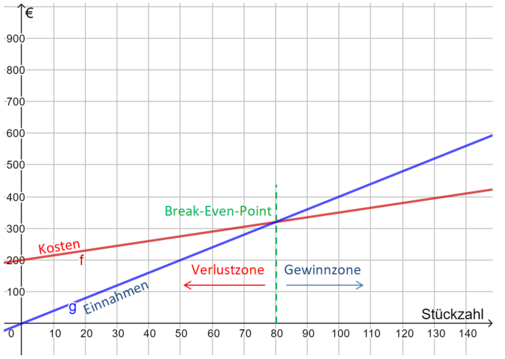
Um bei einer Produktion festzustellen, ab wann die Firma einen Gewinn erzielt, müssen die Kosten mit den Erlösen (Einnahmen) verglichen werden. Der Break-Even-Point ist der Punkt, an die Einnahmen und Kosten gleich hoch sind. An dieser Stelle wird kein Gewinn aber auch kein Verlust erwirtschaftet, da die Kosten und die Erlöse genau gleich sind. Ab hier beginnt also die Gewinnzone.

Übung 1: Vergleich von Handytarifen

Du hast zwei Handytarife zur Auswahl:

Tarif 1: 10€ Grundgebühr und 0,15€ pro Einheit
Tarif 2: 20€ Grundgebühr und 0,05€ pro Einheit
Welche Fragen kannst du an diese Aufgabe stellen?
Wie hilft dir die Mathematik, diese Fragen zu beantworten?

Tipp: Verwende verschiedene Darstellungsmöglichkeiten.

Mögliche Frage:

• Wie viel muss ich im Tarif 1 bezahlen, wenn ich 10 Einheiten telefoniere, wie viel in Tarif 2?
• Ab wie viel Einheiten lohnt sich welcher Tarif?
• ...

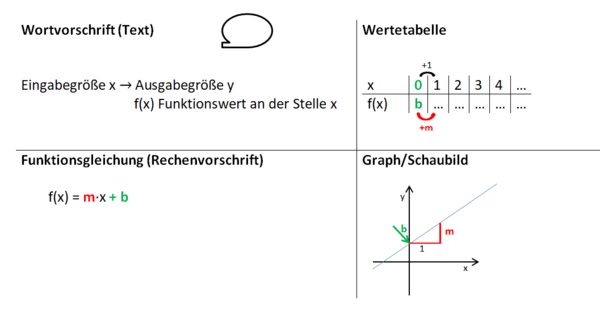
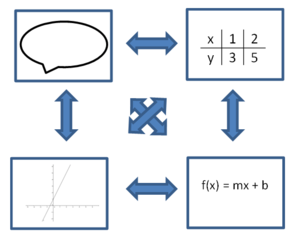
Du kennst 4 verschiedene Dartellungsweisen: Als Text, als Wertetabelle, als Gleichung und als Schaubild. Der Text ist in der Aufgabestellung gegeben.

Erstelle nun eine Wertetabelle, gib die Funktionsgleichung an und zeichne die Schaubilder in ein Koordinatenkreuz. Wähle die Achseneinteilung sinnvoll.

Erstelle eine Wertetabelle. Welche Größen werden einander zugeordnet?

Setze ausgewählte Werte für die Anzahl der Einheiten ein und berechne die Kosten.

Die Zuordnung Anzahl der Einheiten → Kosten(€) ist linear, also hat die Funktionsgleichung die Form
f(x) = mx + b
mit der Steigung m und dem y-Achsenabschnitt b.
Der y-Achsenabschnitt b entspricht jeweils der Grundgebühr, denn auch wenn 0 Einheiten telefoniert werden, müssen diese Kosten bezahlt werden.

Die Steiung m entspricht den Kosten pro Einheit, denn pro telefonierter Einheit steigen die Kosten um den entsprechenden Betrag.

Wähle eine geeignete Einteilung der Achsen:
Welche Größe wird an der x-Achse abgetragen? Die Anzahl der Einheiten.

Welche Größe wird an der y-Achse abgetragen? Die Kosten in €

Wähle auf die x-Achse 1cm für 10 Einheiten und auf der y-Achse 1cm für 5€, also 1mm für 0,50€

Anzahl der Einheiten	0	10	20	30	...
Kosten Tarif 1 (€)	10	11,50	13,00	14,50	...
Kosten Tafrif 2(€)	20	20,50	21,00	21,50	...

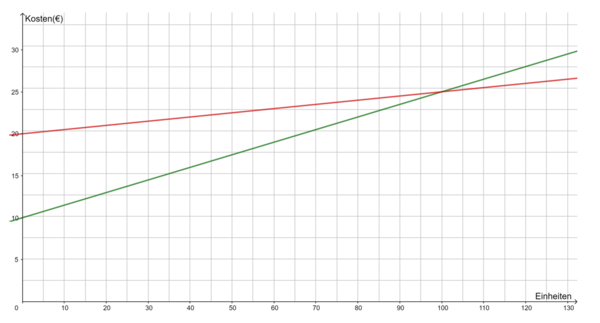
Tarif 1: f(x) = 0,15x + 10
Tarif 2: f(x) = 0,05x + 20
Nun kannst du das Gleichungssystem mit dem Gleichsetzungsverfahren lösen!
I. y = 0,15x + 10
II. y = 0,05x + 20
I = II: 0,15x + 10 = 0,05x + 20   |-10
         0,15x = 0,05x + 10   |-0,05x
          0,1x = 10           |:     0,1 oder ·10 (mit Kehrbruch multiplizieren)
             x = 100
Setze x = 100 in eine der Gleichungen ein:
y = 0,15 · 100 + 10    = 25
Die Kosten für 100 Einheiten sind bei beiden Tarifen gleich, sie betragen 25€.

Bei weniger Einheiten ist der Tarif 1 günstiger, bei mehr Einheiten Tarif 2.

Die beiden Geraden scheiden sich im Punkt S(100|25).
Die Kosten für 100 Einheiten sind bei beiden Tarifen gleich, sie betragen 25€.

Bei weniger Einheiten ist der Tarif 1 günstiger, bei mehr Einheiten Tarif 2.

Übung 2: Stromversorgung - Angebote vergleichen

Familie Winter liegen Angebote von zwei Stromanbietern vor.
   Angebot 1: Grundgebühr 50,80€; Kosten pro kWh 34,4 ct
   Angebot 2: Grundgebühr 75,20€; Kosten pro kWh 30,6 ct
Welchen Tarif empfiehlst du der Familie Winter?
Welche Bedingungen berücksichtigst du?

1. Gib die Bedeutung der Variablen x und y an:
x = Verbrauch (kWh); y = Gesamtkosten (€)

2. Stelle die Funktionsgleichungen für die beiden Angebote auf:
I. ...
II. ...
3. Zeichne die Geraden für beide Funktionen in ein Koordinatenkreuz. x-Achse: 1cm für 100kWh; y-Achse: 1cm für 100€
4. Was kannst du alles ablesen?

2. Die Kosten setzen sich zusammen aus der Grundgebühr und den Kosten pro Kilowattstunde. Achte hier auf gleiche Einheiten, in diesem Fall rechne in Euro:
I. y=0,344·x+50,80
II. y=0,306·x+75,20
Um die Graphen zu zeichnen, rechne für einige x-Werte die zugehörigen y-Werte aus und zeichne diese in ein Koordinatenkreuz. Da es sich um lineare Funktionen handelt, sind die Graphen jeweils Geraden. Du musst also nur 2 Punkte ermitteln.
Für x = 0 gilt
I. y = 0,344·0 + 50,80 = 50,80 (Erinnerung: Das ist der y-Achsenabschnitt b)
II. y = 0,306·0 + 75,20 = 75,20

Berechne ebenso die Werte für z.B. x = 100 (oder x = 200) ...

Die Graphen siehst du im Bild. (Hier wurde mit GeoGebra gezeichnet, dieses Programm kannst du zur Überprüfung deiner Ergebnisse immer nutzen.

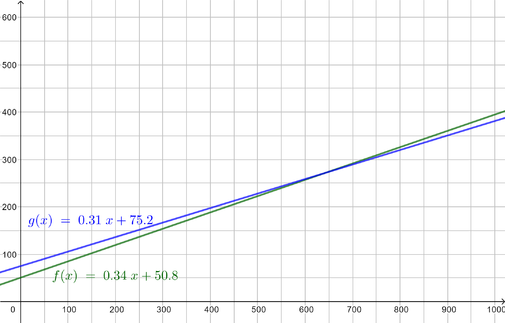
Rechnerische Lösung: Es bietet sich das Gleichsetzungsverfahren an,da beide Gleichungen nach y aufgelöst sind.
I.=II. 0,344x+50,80 = 0,306x+75,20 I-50,80
0,344x = 0,306x+24,40 I-0,306x
0,038x = 24,40 I:0,038
x$\approx$642,1

Die Gesamtkosten berechnest du, indem du x=642 in Gleichung I oder II einsetzt.

Übung 3: Autovermietung

Eine Autovermietung hat folgende Tarife zur Auswahl:

Tarif 1: 45€ tägliche Grundgebühr und 0,45€ pro gefahrener km
Tarif 2: 30€ tägliche Grundgebühr und 0,60€ pro km gefahrener km.

• Stelle für die Tarife jeweils eine Funktionsgleichung auf. (x-Fahrstrecke; y tägliche Kosten)
• Zeichne die Graphen der Funktionen in ein Koordinatensystem. (x-Achse: 1cm sind 10km; y-Achse: 1cm sind 10€)
• Wann kosten beide Tarife gleich viel? Wann ist Tarif 1 bzw. Tarif 2 günstiger?

Es liegt eine lineare Zuordnung vor: gefahrene Kilometer → Kosten
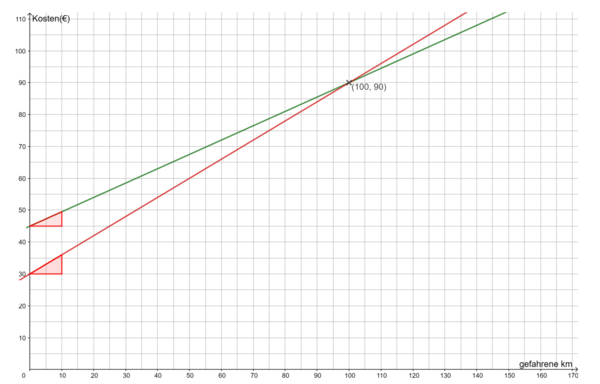
Tarif 1: y = 0,45x + 45

Tarif 2: y = 0,30x + 30

Um deine Zeichnung zu überprüfen, nutze GeoGebra.
Zeichne zunächst den y-Achsenabschnitt b in das Koordinatenkreuz, also
Tarif 1: b = 45
Tarif 2: b = 60
Von hier aus zeichne jeweils die Steigung m mithilfe des Steigungsdreiecks ein. Pro 10km zahlst du 4,50€ mehr, gehe also 10km (1cm) nach rechts und 4,50€ (0,45cm) nach oben. Da dies schwer zu zeichnen ist, kannst du auch 20km (2cm) nach rechts gehen und 9€(0,9cm) nach oben.
Verfahre bei Tarif 2 ebenso.

(Du kannst auch mithilfe einer Wertetabelle je einen zusätzlichen Wert zu den Tarifen ausrechnen und die Geraden durch den y-Achsenabschnitt und den berechneten Punkt zeichnen.)

Übung 4: Busunternehmen

Ein Busunternehmen hat einen Bus für 325000€ gekauft. Der Unternehmer kalkuliert pro Kilometer 0,27€ Betriebskosten. Der Erlös pro Kilometer beträgt durchschnittlich 1,10€.
a) Stelle den Sachverhalt graphisch dar.
b)Ab welcher Fahrstrecke gleichen sich Kosten und Erlös aus?
c) Stelle weitere Fragen an diese Aufgabe und beantworte diese.

1. Gib die Bedeutung der Variablen x und y an:
x = gefahrenen Kilometer; y = Gesamtkosten (€)

2. Stelle die Funktionsgleichungen für die beiden Angebote auf:
I. ...
II. ...
3. Zeichne die Geraden für beide Funktionen in ein Koordinatenkreuz. x-Achse: 1cm für 10000km; y-Achse: 1cm für 10000€
4. Was kannst du alles ablesen?

2. Die Kosten setzen sich zusammen aus dem Kaufpreis und den Kosten/dem Erlös pro Kilometer.
I. y=0,27·x+325000 (Kosten)

II. y=1,10·x (Erlös)

Die Graphen siehst du im Bild. (Hier wurde mit GeoGebra gezeichnet, dieses Programm kannst du zur Überprüfung deiner Ergebnisse immer nutzen.

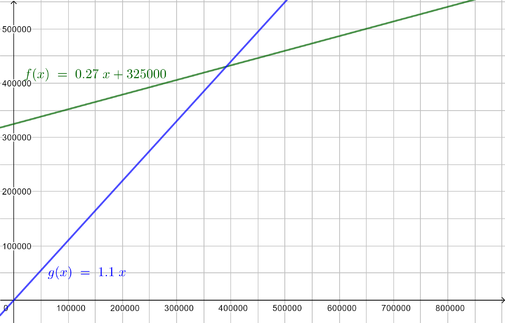
Rechnerische Lösung: Es bietet sich das Gleichsetzungsverfahren an,da beide Gleichungen nach y aufgelöst sind.
I.=II. 0,27x+325000=1,10x I-0,27x
325000=0,83x I:0,83
391566,3$\approx$x
Nach ca. 391600 km übersteigt der Erlös die Kosten.

Die Gesamtkosten berechnest du, indem du x=391566 in Gleichung I oder II einsetzt.

Angebot und Nachfrage - Preisbildungsmodell

Die nachfolgenden Videos erklären das Preisbildungsmodell:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

 

Angebot und Nachfrage - Begriffe

Löse den Lückentext zu den Begriffen "Angebot" und "Nachfrage"

Das Angebot entspricht der Menge Gütern und Dienstleistungen, die an einem Markt dargeboten werden. Die Nachfrage entspricht der Bereitschaft der Konsument*innen, diese Güter und Dienstleistungen zu kaufen. Wie viel angeboten und wie viel nachgefragt wird, ist abhängig vom Preis.

Ähnlich wie im 1. Video das Beispiel des Fischverkaufes auf einem Markt erklärt wurde, bearbeite nun ein weiteres Beispiel.

Angebot und Nachfrage - Beispiel Pizza

Die Tabelle zeigt die Nachfrage nach Pizza in einer Stadt. Vorsicht: Der Preis ist mathematisch der y-Wert (!) auch wenn er hier zuerst genannt wird. Dementsprechend ist die y-Achse die Achse für den Preis.(Im Mathematikunterricht wird immer zuerst die x-Achse genannt, hier musst du umdenken.)

Preis (€)	Nachfrage (Stück)	Angebot (Stück)
3	135	26
4	104	53
5	81	81
6	68	98
7	53	110

• Welche Bedeutung haben die Zeilen der Tabelle? Löse dazu den Lückentext unten.
• Zeichne die Angebotskurve (Gerade) und die Nachfragekurve in ein Koordinatenkreuz. Welche Bedeutung hat der Schnittpunkt der beiden Geraden?

Nachfrage:

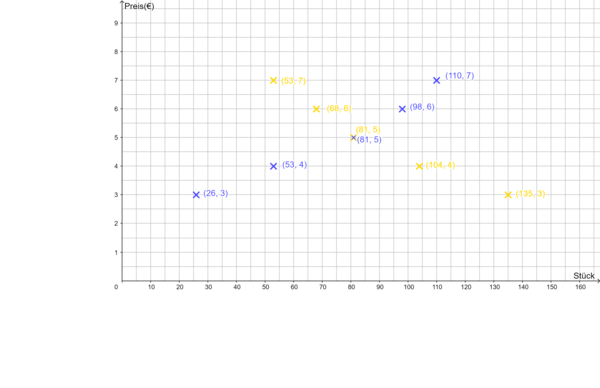
• Wenn der Preis y einer Pizza nur 3€ beträgt, dann ist die Nachfrage x groß, sie beträgt 135 Stück. Du zeichnest also den Punkt (135|3) ins Koordinatenkreuz.
  
• Wenn der Preis einer Pizza 4 € beträgt, sinkt die Nachfrage, sie beträgt dann noch 104 Stück. Du zeichnest also den Punkt (104|4) ins Koordinatenkreuz usw.
  

Angebot:

• Wenn der Preis y einer Pizza nur 3€ beträgt, dann gibt es nicht viele Pizzerien, die dies anbieten, die Angebotsmenge x ist also klein, sie beträgt 26 Stück. Du zeichnest also den Punkt (26|3)ins Koordinatenkreuz.
• Wenn der Preis einer Pizza 4€ beträgt, steigt das Angebot, es sind dann 53 Stück, die angeboten werden. Du zeichnest also den Punkt (4|53) ins Koordinatenkreuz usw.

Beschrifte die Achsen des Koordinatenkreuzes: Auf der x-Achse wird die Anzahl der Pizzen (Stück) eingetragen, auf der y-Achse der Preis (€). Wähle eine geeignete Skala, z.B. 1cm auf der x-Achse entspricht 10 Pizzen; 1cm auf der y-Achse entspricht 1€.

Trage nun die Punkte wie im Lückentext beschrieben ins Koordinatenkreuz ein. Achte darauf, dass du zuerst in x-Achsenrichtung (Anzahl der Pizzen) läufst, dann zum Preis (€), auch wenn dies in der Tabelle anders notiert ist.

Zeichne dann die Angebotskurve (steigende Gerade) und die Nachfragekurve (fallende Gerade) durch die Punkte.

Du kannst durch die eingezeichneten Punkte jeweils näherungsweise ein Gerade zeichnen (Regressionsgerade):

Die beiden Geraden schneiden sich im Punkt S(81|5), was auch schon in der Wertetabelle abzulesen war. Das bedeutet, dass bei einem Preis von 5€ das Angebot von 81 Stück genau zur Nachfrage, die ebenfalls 81 Stück beträgt, passt. Dieser Preis heißt dann "Gleichgewichtspreis".

Angebot und Nachfrage - Beispiel Eis

Die Tabelle zeigt die Nachfrage nach Eiskugeln in einer Stadt.

Vorsicht: Der Preis ist mathematisch der y-Wert (!) auch wenn er hier zuerst genannt wird. Dementsprechend ist die y-Achse die Achse für den Preis.(Im Mathematikunterricht wird immer zuerst die x-Achse genannt, hier musst du umdenken.)

Preis (€)	Angebot (Kugeln)	Nachfrage (Kugeln)
0	0	24
0,25	4	22
0,50	8	20
0,75	12	18
1,00	16	16
1,25	20	14
1,50	12	12
1,75	28	10
2,00	32	8
2,25	36	6
2,50	40	4
2,75	44	2
3,00	48	0

• Welche Bedeutung haben die Zeilen der Tabelle? Löse dazu den Lückentext unten.
• Zeichne die Angebotskurve (Gerade) und die Nachfragekurve in ein Koordinatenkreuz. Welche Bedeutung hat der Schnittpunkt der beiden Geraden?
• Stelle die Funktionsgleichungen der Angebotsfunktion und der Nachfragefunktion auf und berechne den Schnittpunkt.

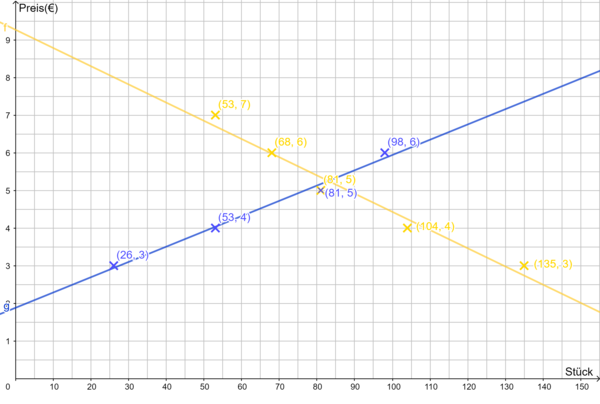
Angebot:

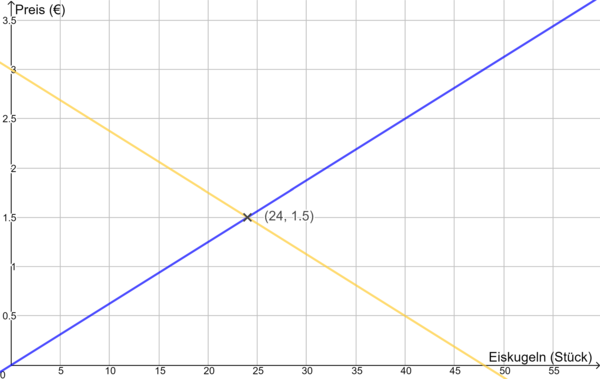
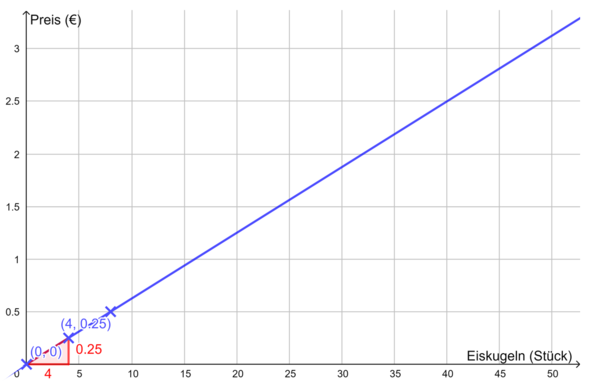
• Wenn der Preis y einer Eiskugel nur 0,25 € beträgt, dann ist das Angebot x klein, es beträgt 4. Wer möchte schon Eis zu einem so niedrigen Preis anbieten? Du zeichnest also den Punkt (4|0,25) ins Koordinatenkreuz.
  
• Wenn der Preis einer Eiskugel 1€ beträgt, steigt das Angebot, es beträgt dann 16. Du zeichnest also den Punkt (16|1) ins Koordinatenkreuz usw.
  

Nachfrage:

• Wenn der Preis y einer Eiskugel nur 0,25€ beträgt, dann ist die Nachfrage x groß, sie beträgt 48. Du zeichnest also den Punkt (44|0,25)ins Koordinatenkreuz.
• Wenn der Preis einer Eiskugel 2€ beträgt, sinkt die Nachfrage, es sind dann 12. Du zeichnest also den Punkt (12|2) ins Koordinatenkreuz usw.

Um die Funktionsgleichungen aufzustellen, benötigst du mathematisches Wissen zu linearen Funktionen.
Dies soll hier wiederholt werden:

Erinnerung: Lineare Funktionen - Funktionsgleichung

Lineare Funktionen sind immer Geraden und haben immer die Form y = mx + b.
Dabei ist m die Steigung der Geraden. Diese kannst du mithilfe eines Steigunsdreieckes ablesen oder mithilfe zweier Punkte berechnen.
Der Parameter b ist der y-Achsenabschnitt, hier wird die y-Achse geschnitten, die x-Koordinate ist also dort immer 0.

Und nun zurück zur Aufgabe:

Die Angebotsgleichung hat die Form y = mx + b, du benötigst also m und b.
① Bestimme b:
b ist der y-Achsenabschnitt, also der y-Wert für x = 0. Dies kannst du in der Wertetabelle ablesen. Schau, wie hoch der Preis ist bei dem Angebot x = 0. (Lösung: Punkt P(0|0)
② Bestimme m:
Für m benötigst du ein Steigungsdreieck. Beginne dies beim Schnittpunkt mit der y-Achse und gehe dann zum nächsten Punkt. Du berechnest m dann mit m = $\tfrac{\text{Höhenunterschied}}{\text{Horizontalunterschied}} = \tfrac{\Delta y}{\Delta x} = \tfrac{y_2-y_1}{x_2-x_1}$
Hier rechnest du also m =$\tfrac{0,25-0}{4-0} = \tfrac{1}{16}$
Die Gleichung für die Angebotsfunktion lautet also: y = $\tfrac{1}{16}$x

Auf die Nachfragegleichung die Form y = mx + b, du benötigst also m und b.
① Bestimme b:
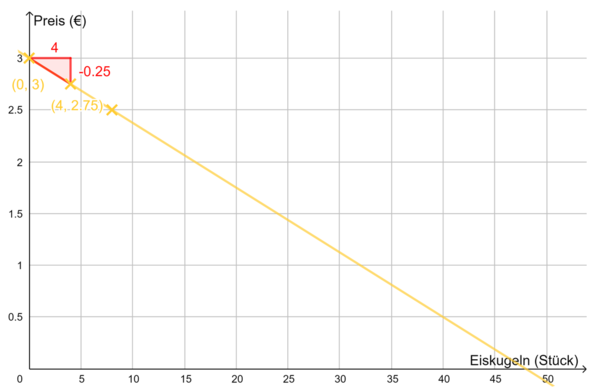
b ist der y-Achsenabschnitt, also der y-Wert für x = 0. Dies kannst du in der Wertetabelle ablesen. Schau, wie hoch der Preis ist bei der Nachfrage x = 0. (Lösung: Punkt P(0|3)
② Bestimme m:
Für m benötigst du ein Steigungsdreieck. Beginne dies beim Schnittpunkt mit der y-Achse und gehe dann zum nächsten Punkt. Du berechnest m dann mit m = $\tfrac{\text{Höhenunterschied}}{\text{Horizontalunterschied}} = \tfrac{\Delta y}{\Delta x} = \tfrac{y_2-y_1}{x_2-x_1}$
Hier rechnest du also m =$\tfrac{2,75-3}{4-0} = \tfrac{-0,25}{4} = -\tfrac{1}{16}$
m ist negativ, dies ist sinnvoll, da die Gerade fällt.
Die Gleichung für die Angebotsfunktion lautet also: y = -$\tfrac{1}{16}$x + 3

Nun kannst du rechnerisch mithilfe des Gleichsetzungsverfahrens den Schnittpunkt der beiden Geraden bestimmen:
Angebot:    I. y = $\tfrac{1}{16}$x
Nachfrage: II. y = -$\tfrac{1}{16}$x + 3
I. = II.
$\tfrac{1}{16}$x = -$\tfrac{1}{16}$x + 3   | +$\tfrac{1}{16}$x
$\tfrac{2}{16}$x = 3             | : $\tfrac{2}{16}$
x = 24
Setze x = 24 in Gleichung I oder II ein, um y zu bestimmen:
x = 24 in I. : y = $\tfrac{1}{16}$·24 = 1,5
Der Schnittpunkt lautet S(24|1,5).