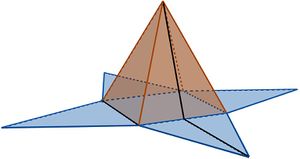
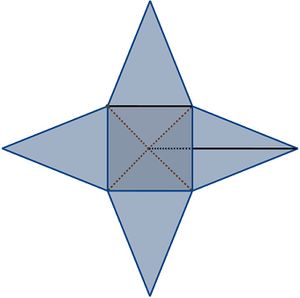
Auf dem Bild siehst du die Karlsruher Pyramide, die auf dem Marktplatz in Karlsruhe steht. Berechne den Oberflächeninhalt (inklusive der Grundfläche), indem du...
Nutze die Personen auf dem Bild als Referenzgröße.
Info
In der Lösung werden die exakten Werte genutzt, deine Ergebnisse können also etwas von dieser Lösung abweichen. Die Lösung kann dir aber als Orientierung dienen.
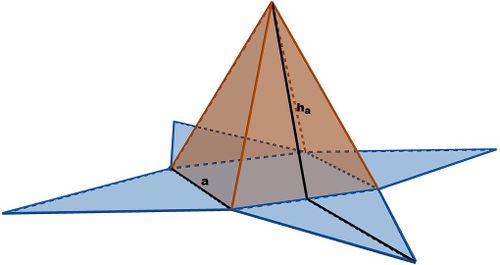
Es gilt  und
und 
Damit gilt dann:
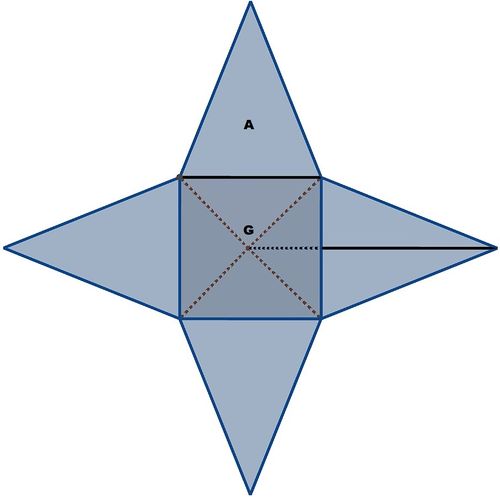
Grundfläche G:


Seitenfläche A:


Mantelfläche M:
Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle M= '''Oberfläche O:''' |Lösung|Lösung verbergen}} |Arbeitsmethode |Farbe=#CD2990}} {{Box|Aufgabe 12|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Kehre nun zum Arbeitsblatt zurück und bearbeite die Aufgabe 12.'''| Arbeitsmethode|Farbe=#CD2990}} ==Vertiefen und Vernetzen== {{Box|Info|In diesem Abschnitt findest du vertiefende Aufgaben zu dem Oberflächeninhalt von Pyramiden und darüber hinausgehenden Themen. Neben Pyramiden kommen in diesem Abschnitt auch weitere Körper bzw. Flächen vor, die du zum Teil bereits aus dem Unterricht kennst. Die Aufgabe 16 ist als Knobelaufgabe gedacht, sodass du hier testen kannst, wie fit du im Umgang mit den Oberflächeninhalten von Pyramiden und ähnlichen Körpern bist.|Kurzinfo}} {{Box|'''Aufgabe 14: Zusammengesetzte Körper'''| [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Kehre zum Arbeitsblatt zurück und bearbeite dort die Aufgabe 14.''' {{Lösung versteckt|Die Dachfläche besteht aus vier Dreiecken, von denen die jeweils gegenüberliegenden gleich groß sind.|Tipp|Tipp verbergen}} {{Lösung versteckt|Wir berechnen als erstes den Oberflächeninhalt des Quaders. Die Grundfläche berechnet sich aus <math>G=a \cdot b=6 \cdot 12=72 \text{ cm}^{²}}
.
Als nächstes wird die Mantelfläche des Quaders berechnet.

Nun berechnen wir die Mantelfläche des Daches. Zunächst berechnen wir die Fläche eines der ersten beiden Dreiecke:
 .
.
Nun fehlt noch die Fläche eines der zweiten beiden Dreiecke:
 .
.
Wir erhalten insgesamt für die Mantelfläche des pyramidenförmigen Daches:
 .
.
Insgesamt erhalten wir also:  .
.
Für 23 Schülerinnen und Schüler muss die Lehrkraft also

Papier mitbringen.