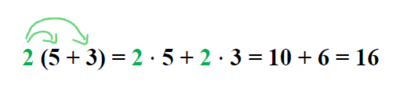Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme
In diesem Lernpfadkapitel lernst du Grundlagen über Terme und binomische Formeln kennen. Im ersten Teil geht es darum, Terme zusammenzufassen. Danach wiederholst du das Ausmultiplizieren und Faktorisieren und im letzten Teil die binomischen Formeln. Lege dir für die Aufgaben Zettel und Stifte bereit. Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit grünem Streifen sind Knobelaufgaben.
Inhaltsverzeichnis
1) Terme zusammenfassen
Einführung
Terme enthalten unterschiedliche Rechenoperationen wie Addition, Subtraktion, Multiplikation und Division. Manche Teile von Termen kann man zusammenfassen, um so den Term zu vereinfachen. Beachte dabei:
Beim Zusammenfassen von Summen gilt:
Nur gleiche Variablen in der gleichen Potenz dürfen zusammengefasst werden.
Beispiele:
1)
2)
Hier konnten nur die beiden Teile mit zusammengefasst werden, da alle anderen Variablen unterschiedlich sind bzw. in einer anderen Potenz vorkommen.
3)
Tipp: Es kann helfen die gleichen Potenzen und Variablen farblich zu markieren.
Beim Zusammenfassen von Produkten gilt:
Es können auch Teile mit unterschiedlichen Potenzen oder Variablen zusammengefasst werden.
Beispiel:
4)
Beachte die Vorzeichen der Faktoren.
Beispiel:
5)
Aufgaben
Fasse die folgenden Terme zusammen. Nutze dazu deinen Zettel und Stift, um die Rechenwege und Lösungen aufzuschreiben.
a)
b)
c)
d)
e)
f)
g)
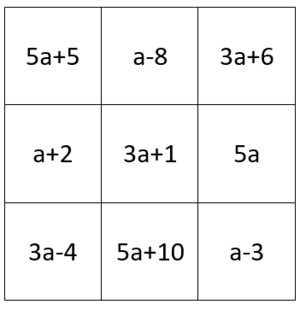
Die Summen jeder Zeile, Spalte und Diagonale des magischen Quadrats ergeben gleichwertige Terme, das heißt wenn du eine Zeile addierst, kommt das gleiche raus wie bei allen anderen Zeilen, Spalten und Diagonalen. Ergänze die fehlenden Terme. Du kannst sie direkt unten eintragen und deine Antwort überprüfen.
| 5a+5 | a-8()
|
3a+6()
|
| a+2 | 3a+1 | 5a()
|
| 3a-4 | 5a+10()
|
a-3()
|
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Das Ausmultiplizieren hat zum Ziel, eine Klammer aufzulösen. Um einen Faktor (im Bsp. 2) mit einer Klammer, in der eine Summe oder Differenz steht (im Bsp. 5 + 3), zu multiplizieren, muss der Faktor mit jedem Glied in der Klammer multipliziert werden:
Dies nennt man Distributivgesetz. Es spielt keine Rolle, ob der Faktor links oder rechts von der Klammer steht:
.
Achte darauf, ob in der Klammer eine Summe oder Differenz steht, denn:
.
Die gleichen Rechenregeln gelten für Variablen:
.
Das Distributivgesetz kann man sich auch anhand von Flächen mit den Seitenlängen a, b und c veranschaulichen:
Besonders aufpassen muss man bei Minusklammern, also wenn vor der Klammer ein negativer Faktor steht. Denn dann drehen sich die Vorzeichen von jedem Glied in der Klammer um:
.
.
Hierfür gilt:
ergibt:
ergibt:
Zwei Summen (oder Differenzen) werden miteinander multipliziert, indem man jeden Summanden der ersten Klammer mit jedem Summanden der zweiten Klammer multipliziert:
.
.
.
Aufgabe
a)
b)
c)
d)
e)
f)
g) =
h) =
Terme faktorisieren
Um zu überprüfen, ob du richtig faktorisiert hast, kannst du eine Probe durchführen, indem du deinen faktorisierten Term ausmultiplizierst und schaust, ob der Ursprungsterm herauskommt.
Du faktorisierst:
Nun prüfst du dein Ergebnis, indem du das Ergebnis ausmultiplizierst:
Aufgabe
Info: Die Teilaufgaben bauen aufeinander auf. Wenn du bei b) oder c) Probleme hast, schau dir nochmal die vorherige(n) Teilaufgabe(n) an.
a) Was lässt sich sinnvollerweise ausklammern?
(i) (!5) (3) (!9) (!x)
(ii) (!9) (12) (!24) (!x)
(iii) (!5) (x) (!y) (!2z)
b) Wie sieht der erste Zwischenschritt beim Ausklammern aus?
(i) (
) (!
) (!
) (!
)
(ii) (
) (!
) (!
) (!
)
c) Klammere komplett aus: (Mache falls du unsicher bist die Probe)
(i) (
) (!
) (!
) (!
)
(ii) (
) (!
) (!
) (!
)
(iii) (!
) (
) (!
) (!
)
Weitere Aufgabenzum Ausmultiplizieren und Faktorisieren
Welche Zahl muss man einsetzen, damit die Umformung stimmt?
a) 3()
b) 15()
c) -12()
d) -5()
e) -4()
7()
In dieser Aufgabe geht es darum, das Gelernte möglichst schnell anzuwenden, denn du trittst gegen den Computergegner an 😉 wer gewinnt das Rennen?
3) Binomische Formeln
Was sind die binomischen Formeln?
Die folgenden drei Umformungen bilden die sogenannten binomischen Formeln:
Diese Formeln werden dir im Laufe deiner Schulzeit immer wieder begegnen, weshalb du sie unbedingt auswendig können solltest. Falls dir dies schwer fällt, schaue dir folgendes Video dazu an ;)
Herleitung der binomischen Formeln
Versuche, die erste binomische Formel in deinem Heft rechnerisch herzuleiten.
Stelle dazu eine Gleichungskette der Form auf.
Nun wird die Potenz ausgeschrieben
Als nächstes werden die Klammern ausmultipliziert
Das Kommutativgesetz (Vertauschungsgesetz) liefert das Ergebnis:
Neben der rechnerischen Lösung gibt es noch eine anschaulichere Möglichkeit, die binomischen Formeln herzuleiten. Dies gelingt über das Vergleichen von Flächen. Ziehe in der unteren Grafik die Punkte an den Balken nach rechts oder links, um die Werte von a und b zu verändern. Beobachte, was das Vergrößern bzw. Verkleinern dieser Werte geometrisch und rechnerisch bewirkt.

Bisher hast du lediglich die Herleitung der ersten binomischen Formel kennengelernt. Die Herleitungen der zweiten und dritten binomischen Formel erfolgen sehr ähnlich und werden hier nicht thematisiert. Falls du dich trotzdem dafür interessierst, schau doch gerne mal bei Serlo vorbei:
https://de.serlo.org/mathe/terme-gleichungen/terme-variablen/binomische-formelnBeispiele
Falls du dich mit den binomischen Formeln noch nicht vertraut genug fühlst, hast du hier die Möglichkeit, anhand von einigen Beispielen dein Verständnis zu fördern. Andernfalls kannst du direkt zum Aufgabenteil übergehen :)
Für a und b können verschiedene Zahlen eingesetzt werden:
a)
Für a und b können auch andere Variablen eingesetzt werden:
b)
Selbst längere Terme kann man für a und b einsetzen:
a)
Die Reihenfolge der Variablen in der Klammer kann manchmal verkehrt herum sein. In diesem Fall wird zunächst das Kommutativgesetz verwendet, bevor die binomische Formel angewendet wird:
b)
a)
Es spielt keine Rolle, ob zuerst die Summe oder die Differenz erscheint (Assoziativgesetz):
b)
Aufgabenteil
| 1. binomische Formel | |||
| 2. binomische Formel | |||
| 3. binomische Formel | |||
| Das ist keine binomische Formel |
a)15()
a()
b)3a()
4b()
3a()
4b())
c)9u()
2()
d)2m()
7()
e)8y()
10z()
f)6u()
17w()
6u()
17w())
Gegeben sind nun allgemein zwei aufeinander folgende natürliche Zahlen und
mit
.
Begründe unter Verwendung einer binomischen Formel, dass die folgende Rechenregel immer stimmt:
Die Differenz ist gleich der Summe
. Notiere deinen Lösungsweg in dein Heft.
Dann wird für
Nun die erste Klammer auflösen:
Schließlich für
Alternativ: