Benutzer:Frau Raunitschke/Terme Klasse 8/Gleichungen lösen
SEITE IM AUFBAU!!
1.1) Was ist eine Gleichung
1.2) Gleichungen lösen durch Probieren
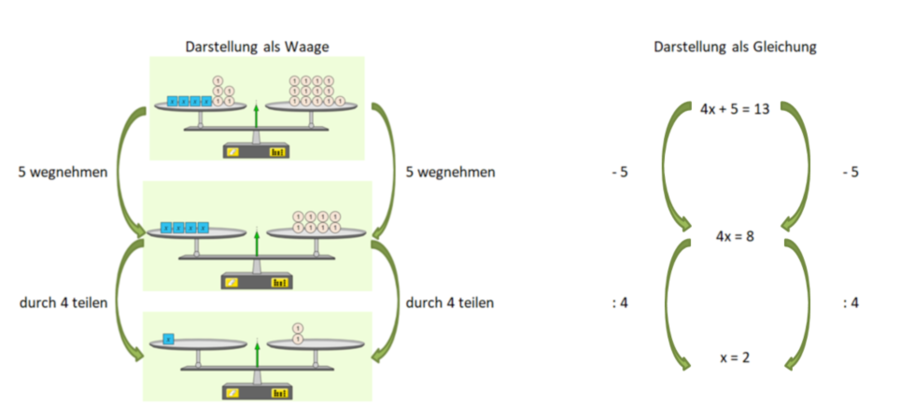
2) Gleichungen lösen durch Umformen
3) Gleichungen mit Klammern
2) Gleichungen lösen durch Umformen
Erklärung des Tricks:
Warum? Das kannst du bald erklären...

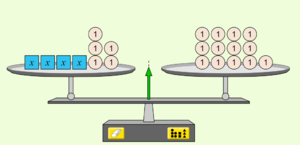
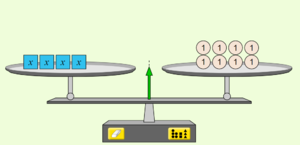
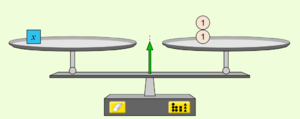
Du hast im letzten Kapitel Gleichungen durch Probieren gelöst. In diesem Kapitel lernst du Möglichkeiten kennen, die Gleichung durch Umformungen zu lösen. Wiederhole dazu die Vorstellungen zu Gleichungen anhand von Waagen im Gleichgewicht in der nachfolgenden LearningApp.
App von G. Plaschke
2.1 Tütengleichungen - Waagemodell
Hilfe zum Finden von schwierigen Gleichungen:
Gehe rückwärts vor: Die Lösung soll z.B. x = 2 sein, also sollen in einer Tüte 2 Steine liegen. Die Gleichung lautet also
x = 2
Nun ergänze auf beiden Seiten immer das Gleiche, bis eine schwierige Gleichung entstanden ist, z.B.
auf beiden Seite zwei Steine ergänzen
x+2 = 4
auf beiden Seiten ein x oder eine Tüte ergänzen
2x + 2 = x + 4
auf beiden Seiten noch eine Tüte ergänzen
3x + 2 = 2x + 4
Diese Umformungen heißen "Äquivalenzumformungen" (von lat. äqui - gleich und vale - wert sein).
2.2 Gleichungen mit Variablen auf einer Seite lösen
Klicke auf das Bild, dann siehst du, wie du die Mengenklammer für die Lösung schreibst. Übe so lange, bis du diese Klammer ebenso schreiben kannst.
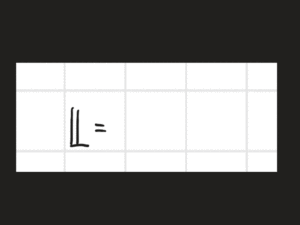
2.3 Gleichungen mit Variablen auf beiden Seiten lösen
Sicherlich kennst du noch die Vorrangregeln beim Berechnen von Termen:
- Punktrechnung vor
- Strichrechnung
Möchtest du nun eine Gleichung nach x auflösen, ist das Ziel, dass x "allein auf einer Seite" der Gleichung steht. Du musst also "alles, was stört auf die andere Seite bringen".
Bei den Umformungen musst du diese Reihenfolge "rückwärts" beachten:
Bringe zunächst die Terme mit Strichrechnung auf die andere Seite, dann löse die Punktrechnung auf.
Noch mehr Übungen (mit Lösungen) findest du hier:
Mathe-Trainer: Lineare Gleichungen
- ↑ Die Bildausschnitte stammen von der Simulation zu Gleichungen auf der Seite von PhET https://phet.colorado.edu/sims/html/equality-explorer/latest/equality-explorer_de.html