Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Punkte und Vektoren im Raum

Info

In diesem Lernpfadkapitel beschäftigst du dich mit Punkten und Vektoren im Raum. Du lernst die Grundlagen zum Thema Punkte und Vektoren. Dies Beinhaltet die Unterscheidung dieser beiden Begriffe, das Rechnen, Interpretieren und Anwenden im Sachzusammenhang.

Dazu haben wir für dich Aufgaben in verschiedenen Schwierigkeitsstufen:

• Mit Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in blauer Farbe sind Aufgaben mittlerer Schwierigkeit
• und Aufgaben mit grünem Streifen sind Knobelaufgaben.

Wir wünschen dir viel Erfolg!

Wiederholung von Punkten und Vektoren

Erinnerung: Punkte und Ortsvektoren

Jeder Punkt lässt sich durch den Vektor beschreiben, der den Ursprung auf diesen Punkt verschiebt, den Ortsvektor. Bei Punkten werden die Koordinaten direkt an den Namen des Punktes  geschrieben, der Name des Punktes wird immer groß geschrieben; bei Vektoren, also auch bei Ortsvektoren, werden die Koordinaten durch ein Gleichheitszeichen vom Namen des Vektors getrennt, der Name des Vektors wird manchmal mit einem Pfeil darüber versehen und meistens klein geschrieben.

Zum Punkt $A(1|2|3)$ gehört also der Ortsvektor $\vec {a} = \begin{pmatrix} 1 \\ 2 \\ 3 \end{pmatrix}$.

{{Box|1= Aufgabe 1: Koordinatensysteme|2= Für diese Aufgabe benötigst du einen Bleistift, ein kariertes Blatt Papier und ein Geodreieck. Bearbeite die folgenden Aufgaben.

1. Zeichne ein dreidimensionales Koordinatensystem. Wähle eine passende Skalierung anhand der angegebenen Punkte im Aufgabenteil 2 und 3.
2. Zeichne die Punkte $A (1|2|1)$,$B(1|4|2)$, $C(1|2|{-}1{,}5)$ und $D(1|4|{-}0{,}5)$ in das gezeichnete Koordinatensystem. Zeichne nun die Strecken $\vec{ AB }$ , $\vec{ AC }$,$\vec{ CD }$ und $\vec{ BD }$ ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn.
3. Nutze den Punkt $A (1|2|1)$ aus Aufgabenteil 2. Füge die Punkte $E (-1|2|1)$,$F(1|0|1)$, $G(-1|0|1)$ und $H(0|1|5)$. Zeichne nun die Strecken $\vec{ AE }$,$\vec{ AF }$, $\vec{ AH }$, $\vec{ EG }$, $\vec{ AH }$, $\vec{ FG }$, $\vec{ FH }$ und $\vec{ GH }$ ein. Handelt es sich um eine zweidimensionale Figur oder um einen Körper? Benenne sie oder ihn.

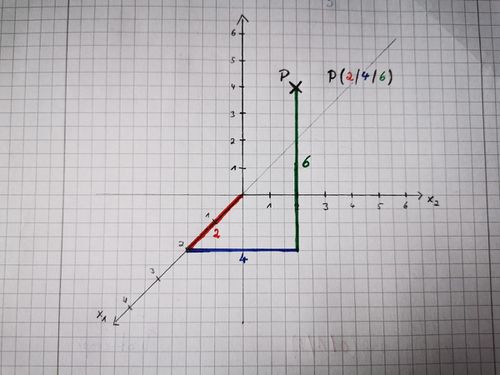
Punkte in einem dreidimensionalen Koordinatensystem kannst du mithilfe eines "Pfad-Folge-Verfahren" genau bestimmen. Dabei geht man die durch die Punktkoordinaten angegeben Längeneinheiten in die Richtung der jeweiligen Achsen. Es entsteht einen Koordinatenzug. Das folgende Bild verdeutlicht das Verfahren.

{{Lösung versteckt|1= Bei Aufgabenteil 2 handelt es sich um ein Parallelogram. Bei Aufgabenteil 3 bekommst du eine Pyramide heraus, die eine quadratische Grundfläche besitzt. Deine Lösung kann aufgrund einer anderen Skalierung der Achsen natürlich auch von der folgenden Lösung abweichen.

Aufgabe 3: Geometrische Objekte im Koordinatensystem

Die abgebildete Pyramide besitzt einen einen Eckpunkt im Nullpunkt $A(0|0|0)$. Welche Aussagen stimmen mit den abgebildeten Punkten überein?

Welche Aussage stimmt für die Koordinaten der Punkte $B$,$C$ und $D$  ?

	$B (5|0|0),C(0|0|5),D(0|5|0)$
	$B(0|5|0),C(0|5|5),D(0|0|5)$
	$B (5|0|0),C(5|5|0),D(0|5|0)$
	$B (1|0|0),C(0|1|1),D(0|0|1)$

Betrachte jeweils zuerst die x1-Achse, dann die x2-Achse und abschließend die x3-Achse.

Welche Aussage stimmt für die Größe der Grundfläche der Pyramide ?

	Die Größe der Grundfläche der Pyramide beträgt $5 LE^2$.
	Die Größe der Grundfläche der Pyramide beträgt $10 LE^2$.
	Die Größe der Grundfläche der Pyramide beträgt $25 LE^2$.

Die Grundfläche einer Pyramide berechnet man mit durch die Multiplikation zweier Seiten.

Wo liegt der Spitze der Pyramide ?

	Der Scheitelpunkt liegt bei $S (2{,}5|2{,}5|6)$.
	Der Scheitelpunkt liegt bei $S (5|5|5)$.
	Der Scheitelpunkt liegt bei $S (2{,}5|2{,}5|5)$.

Bei der Berechnung des Scheitelpunkts sind die 2 der 3 Koordinaten durch die Bestimmung der Seitenflächen vorgegeben. Dabei solltest du beachten, dass nicht die volle Seitenfläche berechnet wird.

Aufgabe 4: Vektoren

Betrachte die dargestellten Vektoren $\vec{u} = \begin{pmatrix} 0 \\ -2 \\ 1 \end{pmatrix}$, $\vec{v} = \begin{pmatrix} 3 \\ 0 \\ -1 \end{pmatrix}$ und $\vec{w} = \begin{pmatrix} -3 \\ 2 \\ 0 \end{pmatrix}$.

Für den Punkt $\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$ gilt

$\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} + \vec{v} + \vec{u} + \vec{w}$.

Welche Punkte erhältst du bei folgenden Verschiebungen durch die Vektoren.

1. $\begin{pmatrix} 3 \\ 0 \\ 0 \end{pmatrix} + \vec{w}$
2. $\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u}$
3. $\begin{pmatrix} -3 \\ 0 \\ 0 \end{pmatrix} - \vec{w}$
4. $\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} - \vec{u}-\vec{w}-\vec{v}$
5. $\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix} + \vec{v} + \vec{w}+ \vec{u}$
6. $\begin{pmatrix} 0{,}5 \\ 2 \\ 1 \end{pmatrix} + \vec{w} + \vec{u} +\vec{v}$
7. $\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{w}$
8. $\begin{pmatrix} -1 \\ 2 \\ -1\end{pmatrix} + \vec{v} - \vec{v}$
9. $\begin{pmatrix} 1 \\ 2 \\ 0 \end{pmatrix} + \vec{u} - \vec{v} - \vec{w}$
10. $\begin{pmatrix} 1 \\ 4 \\ -1 \end{pmatrix} + 2* \vec{u}$

1. $\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix}$
2. $\begin{pmatrix} 0 \\ 2 \\ 0 \end{pmatrix}$
3. $\begin{pmatrix} 0 \\ -2 \\ 0 \end{pmatrix}$
4. $\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}$
5. $\begin{pmatrix} 1 \\ 1 \\ 1 \end{pmatrix}$
6. $\begin{pmatrix} 0{,}5 \\ 2 \\ 1 \end{pmatrix}$
7. $\begin{pmatrix} 4 \\ -2 \\ 1 \end{pmatrix}$
8. $\begin{pmatrix} -1 \\ 2 \\ -1 \end{pmatrix}$
9. $\begin{pmatrix} 1 \\ -2 \\ 2 \end{pmatrix}$
10. $\begin{pmatrix} 1 \\ 0 \\ 1 \end{pmatrix}$

Aufgabe 5: Ortsvektoren

Aufgabe 6: Gerichtete Größen

Gib das folgende Gesetz mithilfe von Vektoren an: Übt ein Körper $A$ auf einen anderen Körper $B$ eine Kraft aus, so wirkt eine gleich große, aber entgegen gerichtete Kraft von Körper $B$ auf Körper $A$.

Erläutere, inwiefern sich Kräfte durch Vektoren darstellen lassen.

$\vec {F}_{A \to B} = -\vec {F}_{B \to A}$

Sowohl Kräfte als auch Vektoren sind durch eine Richtung und eine Größe gekennzeichnet. Im Fall von Vektoren heißt die Größe der "Betrag" oder die "Länge" des Vektors. Es handelt sich demnach bei beidem um gerichtete Größen.

Aufgabe 7: Länge und Abstände von Vektoren

Berechne die Länge der Vektoren:

1 $\vec{v} = \begin{pmatrix} 12 \\ 3 \\ 4 \end{pmatrix}$

	$11$
	$12$
	$13$
	$14$

2 $\vec{v} = \begin{pmatrix} 1 \\ 0 \\ -1 \end{pmatrix}$

	$1$
	$2$
	$\sqrt{2}$
	$\frac{1}{2}$

Berechne den Abstand der Punkte:

1 $A(8|9|10)$ und $B(2|6|8)$

	$9{,}5$
	$7$
	$8$
	$6{,}5$

2 $A(-1|{-}2|2)$ und $B(-3|{-}1|0)$

	$3$
	$6$
	$9$
	$12$

Aufgabe 8: Vektoren addieren und mit einem Skalar multiplizieren

Aufgabe 9: Lückentext - Geometrische Bedeutung von Vektoraddition und skalarer Multiplikation

Wir definieren zwei Rechenoperationen für Vektoren: das Bilden des Vielfachen und der Summe. Die Vektoraddition bezeichnet das bilden der Summe zweier Vektoren gleichen Typs, das heißt dass die beiden Vektoren gleich viele Komponenten haben. Man bildet die Summe, indem man die Einträge der Vektoren komponentenweise addiert. Wir können uns die Addition von Vektoren als ein „Aneinanderlegen“ von zwei Strecken von ggf. verschiedener Länge vorstellen. Nennen wir $\vec{a}$ und $\vec{b}$ Vektoren. Wir deuten diese als Pfeile und addieren sie, das heißt wir legen sie hintereinander, sodass der Anfang von $\vec{b}$ und die „Spitze“ von $\vec{a}$ übereinstimmen. Ein derartiges Verhalten von Pfeilen ist aus der Physik bekannt. Dort werden oftmals Kräfte und Geschwindigkeiten mit Pfeilen dargestellt. Man kann am Ende zur Addition sagen, dass das Bilden der Summe zweier Vektoren $\vec{a} + \vec{b}$ als Hintereinander-Ausführen der durch $\vec{a}$ und $\vec{b}$ dargestellten Verschiebungen gesehen werden kann.

Das Bilden des Vielfachen eines Vektors wird auch als Multiplikation mit einem Skalar bezeichnet. Wir nennen unseren Vektor wieder $\vec{a}$ und das Skalar bezeichnen wir mit $c$. Von jedem Vektor kann das $c$ -Fache gebildet werden, indem alle Komponenten von $\vec{a}$ mit $c$ multipliziert werden. Ist $c>0$ so wird der „Pfeil“ von $\vec{a}$ um den Faktor $c$ aufgeblasen (falls $c > 1$) oder geschrumpft (falls $c < 1$ ). Ist $c<0$, so erhält der Pfeil, der um den Faktor $c$ aufgeblasen oder geschrumpft wird, noch eine Richtungsumkehrung. Für den Fall $c=-1$ sprechen wir dann vom Gegenvektor von $\vec{a}$.

Wir nennen zwei Vektoren kollinear (oder parallel), wenn einer der Vektoren ein Vielfaches des anderen ist. Mit anderen Worten: Wenn $\vec{a}$ und $\vec{b}$ zwei verschiedene Vektoren sind, so sind sie parallel/kollinear zueinander, falls ein Skalar $c$ existiert, sodass gilt: $ca=b$. Dabei ist es egal, ob die beiden Vektoren in verschiedene Richtungen zeigen oder nicht.

 

Aufgabe 10: Kollinearität von Vektoren

Aufgabe 11: Besondere Vierecke

In einem kartesischen Koordinatensystem sind die Punkte $A(3|3|5)$, $B(3{,}5|3{,}5|1)$ und $C(6{,}5|2{,}5|3)$ gegeben.

a) Um welche Art von Dreieck handelt es sich?

	rechtwinkliges Dreieck
	gleichseitiges Dreieck
	gleichschenkliges Dreieck

b) Wir betrachten weiterhin das Dreieck $ABC$. Ein neuer Punkt $Q$ soll so gewählt werden, dass er zusammen mit dem Dreieck $ABC$ ein Parallelogramm bildet, das keine Raute ist. Welche Koordinaten passen zu $Q$? Es sind zwei Antwortmöglichkeiten richtig. Finde beide!

	$P(6|2|7)$
	$P(7|4|3)$
	$P(0|4|3)$
	$P(6|3|{-}1)$

Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist.

Du musst Gegenvektoren verwenden.

Verwende den Vektor $\vec{ CA }$ am Punkt $B$ für eines der Parallelogramme und den Vektor $\vec{ BA }$ am Punkt $C$ für das zweite Parallelogramm.

c) Sei $P$ nun ein weiter Punkt im bereits vorhandenen System. Welche Koordinaten muss $P$ haben, damit $P$ gemeinsam mit $A$, $B$ und $C$ die Eckpunkte einer Raute bildet?

	$P(7|3|{-}1)$
	$P(-7|{-}3|1)$
	$P(5|2|{-}3)$
	$P(-5|{-}2|3)$

Fertige eine Skizze des Dreiecks an und mache dir klar, welche Seite die Basis des Dreiecks ist.

In einer Raute sind alle Seiten gleich lang und gegenüberliegende Seiten parallel.

Verwende den Vektor $\vec{ AC }$ am Punkt $B$.