Digitale Werkzeuge in der Schule/Unterwegs in 3-D – Punkte, Vektoren, Geraden und Ebenen im Raum/Geraden im Raum
Im Folgenden findest du...
Einführung
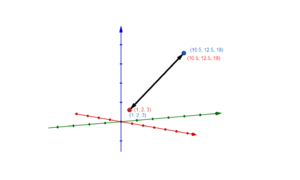
Parameterdarstellung einer Geraden
Lagebeziehungen von Geraden
Im Folgenden wollen wir betrachten, wie verschiedene Geraden zueinander im Raum liegen.
Definitionen
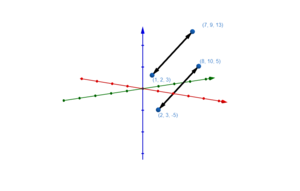
Wir unterscheiden die Lage zweier Geraden in identisch, parallel, geschnitten und windschief. Um die Lage zweier Geraden zu ermitteln, betrachtet man zunächst die Richtungsvektoren. Sind diese zueinander kollinear (sind Vielfache voneinander), so können die Geraden lediglich identisch oder parallel sein.
Um nun zu untersuchen, ob die Geraden parallel oder identisch sind, setzen wir einen Punkt der einen Geraden in die Geradengleichung der anderen Geraden ein. Liegt der Punkt der einen Geraden auf der anderen Geraden, sind die Geraden identisch. Andernfalls sind die Geraden echt parallel.
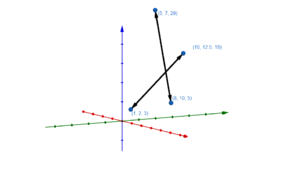
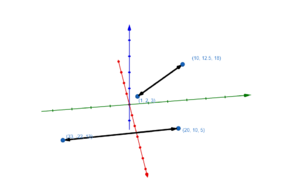
Sind die Richtungsvektoren nicht kollinear, so können die Geraden sich lediglich schneiden oder windschief zueinander sein.
Um nun zu untersuchen, ob sich die Geraden schneiden oder zueinader winschief sind, müssen wir schauen, ob sich ein Schnittpunkt berechnen lässt. Hierzu setzen wir die Geradengleichungen gleich und formen um. Erhalten wir einen Schnittpunkt S, so schneiden sich die Geraden im Punkt S. Andernfalls sind diese Geraden windschief zueinander.
Bevor wir nun zu Sachaufgaben kommen, wollen wir zunächst die Ermittlung der Lage zweier Geraden im Raum zueinander ermitteln.