Benutzer:Buss-Haskert/Trigonometrie/Berechnungen in allgemeinen Dreiecken
SEITE IM AUFBAU
1) Sinus, Kosinus, Tangens
2) Strecken- und Winkelberechnungen in rechtwinkligen Dreiecken
3 Strecken- und Winkelberechnungen in allgemeinen Dreiecken
Die Seitenverhältnisse Sinus, Kosinus und Tanges gelten nur für rechtwinklige Dreiecke.
Um in allgemeinen Dreiecken Strecken und Winkel berechnen zu können, zerlege das Dreieck mithilfe einer Höhe in zwei rechtwinklige Dreiecke.
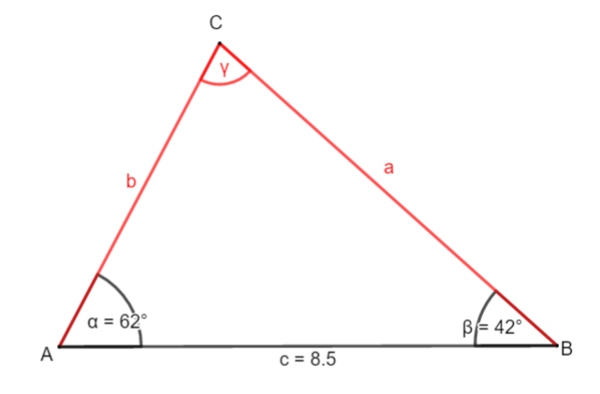
Beispiel 1: Eine Seite und zwei Winkel sind gegeben
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
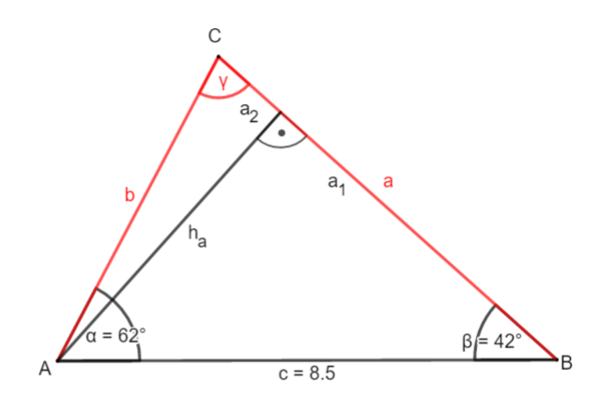
1. Möglichkeit: Zerlege das Dreieck durch die Höhe ha ein zwei rechtwinklige Dreiecke.
② Berechne ha:
sin β = | ·c
c · sin β = ha
8,5 · sin(42°) = ha
5,7 (cm) ha
③ Berechne b:
sin γ = | ·b
b · sin γ = ha | : sin γ
b =
b =
b 5,9 (cm)
④ Berechne a:
cos β = | ·c
c · cos β = a1
8,5 · cos (42°) = a1
cos γ = | ·c
b · cos γ = a2
5,9 · cos (76°) = a2
= 6,3 + 1,4
Beispiel 1: Eine Seite und zwei Winkel sind gegeben
① Bestimme γ:
Winkelsummensatz
γ = 180° - α - β
= 180° - 42° - 62°
= 76°
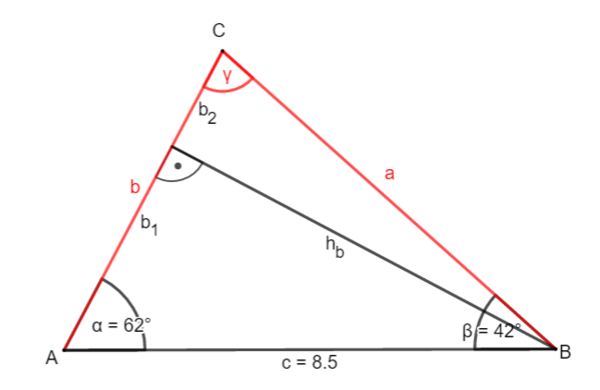
2. Möglichkeit: Zerlege das Dreieck durch die Höhe hb ein zwei rechtwinklige Dreiecke.
② Berechne hb:
sin α = | ·c
c · sin α = hb
8,5 · sin(62°) = hb
7,5 (cm) hb
③ Berechne a:
sin γ = | ·a
a · sin γ = hb | : sin γ
a =
a =
a 7,7 (cm)
④ Berechne b:
cos α = | ·c
c · cos α = b1
8,5 · cos (62°) = b1
cos γ = | ·c
a · cos γ = b2
7,7 · cos (76°) = b2
= 4,0 + 1,9
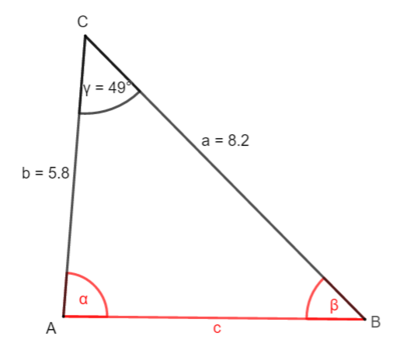
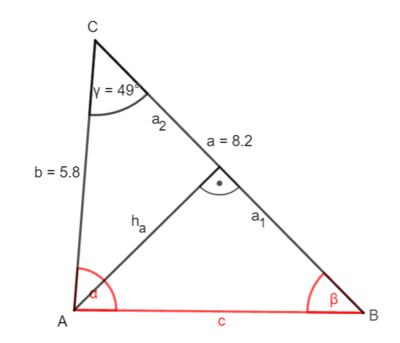
Beispiel 2: Zwei Seiten und ein Winkel sind gegeben
① Bestimme ha:
sin γ = |·b
b · sin γ = ha
5,8 · sin(49°) = ha
4,4 (cm) ha
② Bestimme a2
cos γ = |·b
b · cos γ = a2
5,8 · cos(49°) = a2
3,8 (cm) a2
③ Bestimme a1
a – a2= a1
8,2 - 3,8 = a1
4,4 (cm) = a1
④ Bestimme β
tan β = |
tan β = |tan-1
β 45°
⑤ Bestimme c
c · sin β = ha |: sin β
c =
c =
c=
c 6,2 (cm)
⑥ Bestimme den letzten Winkel α
Winkelsumme
α + β + γ = 180° |- β; -γ
α = 180° - β - γ
α = 180° - 45° - 49°
α = 86°