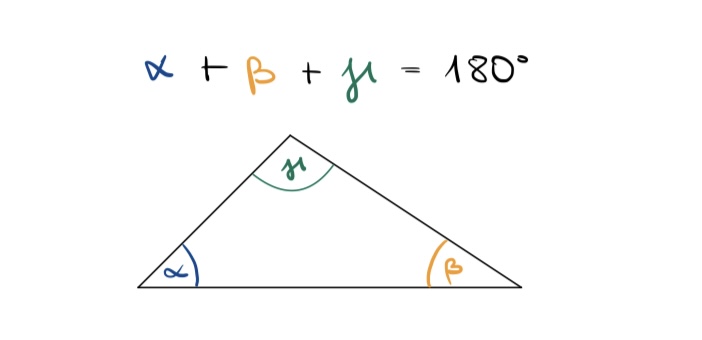Geometrie im Dreieck/Geheimcode der Geometrie

Informationskästchen

Info

In diesem Lernpfadkapitel tauchen wir in die spannende Welt der Dreiecke ein und erforschen die Geheimnisse der Innenwinkelsumme. Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Einführung

Was ist die Innenwinkelsumme in einem Dreieck?

Die Summe der Innenwinkel in einem Dreieck beträgt immer 180 Grad. Dies wird durch den Innenwinkelsatz beschrieben.

Stimmt das auch wirklich? Wenn ja, dann müssten die drei Innenwinkel im Dreieck einen gestreckten Winkel ergeben. Das sollte dann also in etwa so aussehen:

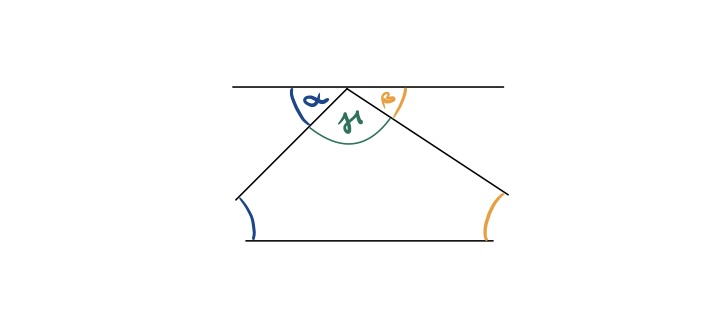
Reiße die zwei Winkel α und β deines Dreiecks (auf dem Arbeitsblatt) ab und prüfe, ob man sie an der Spitze zu einem gestreckten Winkel mit 180° anordnen kann.

Du kannst dies auch an dem GeoGebra Applet ausprobieren und beobachten, ob das auch bei verschiedenen Dreiecken klappt!

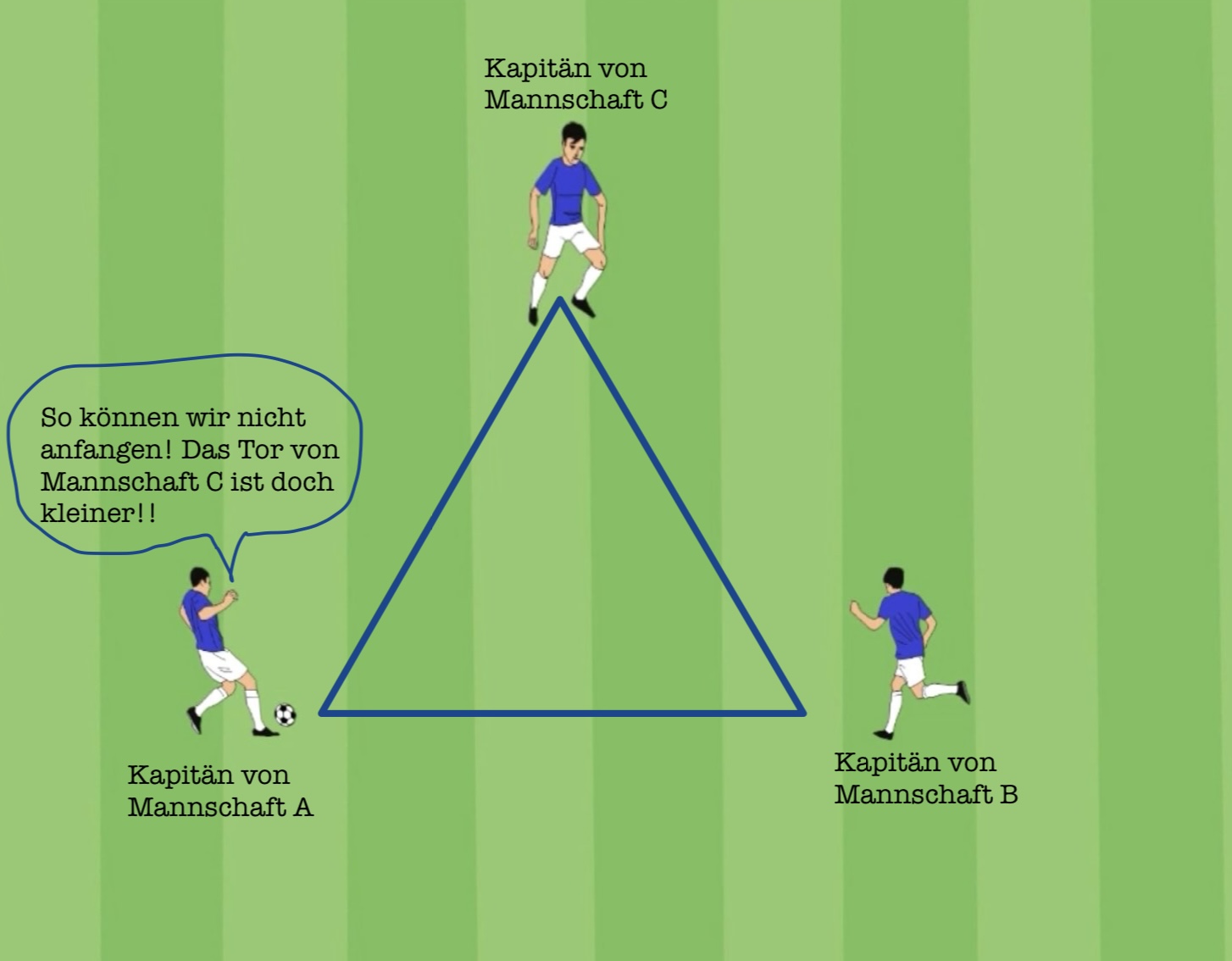
Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht

Winkelberechnung im Ecken-Fußball mit dem Innenwinkelsatz

Die Klasse 8a spielt in der Sportstunde ein Spiel namens Ecken-Fußball. Dafür stellen sie ein Dreieck aus Bänken auf, bei dem jede Ecke ein Tor darstellt. Der Kapitän von Mannschaft A behauptet, dass das Tor von Mannschaft C viel kleiner ist als die anderen. Die Sportlehrerin beruhigt die Klasse und erklärt:,,Ich kann euch versichern, dass das Tor von Mannschaft A einen Winkel von 60° hat und das Tor von Mannschaft B genauso groß ist. Mit eurem Wissen aus dem Mathematikunterricht solltet ihr herausfinden, ob das Tor von Mannschaft C größer oder kleiner ist als die anderen.

Hilf der Klasse 8a, indem du den Winkel des Tores von Mannschaft C berechnest und begründe deine Antwort. Ist das Fußballspiel fair oder nicht?

Lösung

Zusatzfrage

Wenn das Spielfeld so geändert wird, dass der Winkel des Tores von Mannschaft A auf 70° vergrößert wird, wie verändert sich der Winkel des Tores von Mannschaft C? Begründe, ob das Spiel fair ist oder nicht.

Tipp

Lösung

Aufgabe 1

Level 1: Erstere Hinweise

Euer erster Hinweis führt euch zu einem Dreieck, bei dem zwei Winkel gegeben sind: 50° und 60°. Der dritte Winkel ist jedoch verdeckt. Findet den verborgenen Winkel und zeigt rechnerisch, dass die Summe der Innenwinkel 180° beträgt. Die Innenwinkelsumme eines Dreiecks ist immer 180°, weil die drei Winkel zusammen eine gerade Linie ergeben, wenn man sie nebeneinanderlegt. Eine gerade Linie hat immer 180°.

Lösung

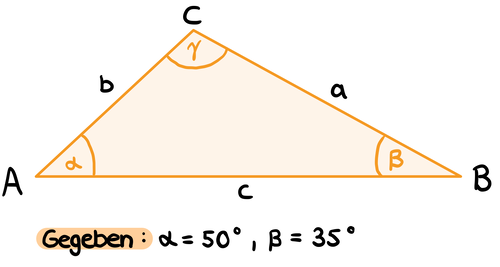
Um den verborgenen Winkel zu finden, nutzen wir die Tatsache, dass die Innenwinkelsumme eines Dreiecks immer 180° beträgt. Die gegebenen Winkel sind 50° und 60°. Der dritte Winkel x lässt sich berechnen, indem wir die Summe der beiden gegebenen Winkel von 180° abziehen: x=180°−(50°+60°) Rechnung: x=180°−110°=70° Ergebnis: Der verborgene Winkel ist 70°. Nachweis der Innenwinkelsumme: 50°+60°+70°=180°

Damit ist rechnerisch bestätigt, dass die Summe der Innenwinkel eines Dreiecks 180° beträgt.

Level 2: Weitere Spuren entdecken

Euer nächster Hinweis befindet sich in einem gleichschenkligen Dreieck. Ihr wisst, dass die beiden Basiswinkel jeweils 65° betragen, aber der Winkel an der Spitze ist unleserlich. Berechnet diesen Winkel und erklärt rechnerisch, warum die Innenwinkelsumme 180° ergibt. Argumentiert, warum die Summe der Winkel im Dreieck immer diese Zahl ergibt, egal wie das Dreieck aussieht.

Lösung

In einem gleichschenkligen Dreieck sind die beiden Basiswinkel gleich. Hier beträgt jeder der beiden Basiswinkel 65°. Um den Spitzenwinkel x zu berechnen, nutzen wir wieder die Innenwinkelsumme eines Dreiecks, die stets 180° beträgt. Rechnung:

Die Summe der beiden Basiswinkel beträgt: 65°+65°=130°

Der Spitzenwinkel x ergibt sich aus: x=180°−130°=50° Der Winkel an der Spitze ist 50°.

Nachweis der Innenwinkelsumme: 65°+65°+50°=180° Damit ist die Innenwinkelsumme des Dreiecks rechnerisch bestätigt.

Warum ist die Summe immer 180°? Die Innenwinkelsumme eines Dreiecks beträgt immer 180°, weil die drei Innenwinkel zusammen eine gerade Linie ergeben, wenn man die Winkel nebeneinander legt. Dies folgt aus den geometrischen Eigenschaften von Dreiecken:

Definition von Winkeln und Linien: Ein gerader Winkel entspricht 180°.

Geometrische Herleitung: Wenn man in einem Dreieck eine der Seiten verlängert, bildet der äußere Winkel zusammen mit dem Innenwinkel an der Basis einen geraden Winkel (180°). Alle Innenwinkel summieren sich daher ebenfalls zu 180°. Egal, wie ein Dreieck geformt ist (spitzwinklig, rechtwinklig, stumpfwinklig), bleibt diese Eigenschaft bestehen, da sie auf den geometrischen Grundlagen basiert.

Level 3: Das letzte Rätsel

Auf dem letzten Teil eurer Jagd entdeckt ihr eine mysteriöse geometrische Nachricht: "In jedem Dreieck steht ein gestreckter Winkel, wenn man die Innenwinkel nebeneinanderlegt." Ihr sollt dies überprüfen, in dem ihr ein eigenes Dreieck konstruiert und die drei Innenwinkel nebeneinander anordnet. Zeigt, dass diese Winkel zusammen einen gestreckten Winkel (180°) ergeben und begründet rechnerisch und logisch, warum dies immer so ist.

Zusatzfrage: Überlegt, ob diese Regel auch für Vierecke gilt und begründet eure Antwort.

Tipp 1

Überlegt euch, wie ihr ein Vieleck in Dreiecke zerlegen könnt. Jedes Dreieck hat eine Innenwinkelsumme von

180°. Die Anzahl der Dreiecke im Vieleck hilft euch dabei, die gesamte Innenwinkelsumme zu berechnen. Probiert es zuerst mit einem Viereck: Wie viele Dreiecke könnt ihr darin erkennen? Dann versucht es mit einem Fünfeck. Die Formel, die euch helfen könnte, lautet: (n−2)⋅180°, wobei n die Anzahl der Ecken des Vielecks ist.

Lösung

Hauptaufgabe: Nachweis der Innenwinkelsumme von 180∘ im Dreieck

1. Konstruktion eines eigenen Dreiecks: Nehmen wir ein Dreieck mit den Innenwinkeln 50°, 60° und 70°.
2. Anordnung der Winkel: Legt die drei Winkel nebeneinander, sodass sie eine gemeinsame Ecke haben. Wenn ihr die Winkel so arrangiert, bilden sie zusammen eine gerade Linie, also einen gestreckten Winkel von 180°.
3. Rechnung: 50°+60°+70°=180°
4. Logische Begründung:
   • Die Innenwinkelsumme eines Dreiecks ergibt sich aus der Geometrie von ebenen Flächen.
   • Ein Dreieck ist die einfachste geschlossene Form in der Ebene. Wenn man alle drei Innenwinkel nebeneinander legt, decken sie zusammen 180° ab, was der Definition eines gestreckten Winkels entspricht.

---

Zusatzfrage: Gilt diese Regel auch für Vierecke?

Nein, für Vierecke gilt diese Regel nicht direkt, da die Innenwinkelsumme eines Vierecks 360° beträgt.

1. Warum 360°? Ein Viereck kann in zwei Dreiecke unterteilt werden, und die Innenwinkelsumme eines Dreiecks ist 180°. Daher ergibt sich für ein Viereck: 180°+180°=360°
2. Begründung: Die Anzahl der Innenwinkel in einem Polygon bestimmt die Summe der Winkel. Für ein n-Eck gilt die Formel: Innenwinkelsumme=(n−2)⋅180°

Für ein Viereck (n=4) ergibt sich: (4−2)⋅180°=360°

Aufgabe 2

Aufgabe 2.1

Berechne den fehlenden Winkel mithilfe des Innenwinkelsatzes!

Tipp

Berechne den fehlenden Winkel γ, indem du die Winkel α und β von 180° abziehst.

Lösung

Aufgabe 2.2

Erkenne die Innenwinkel des Dreiecks und berechne sie!

Tipp 1

α und α' bilden einen rechten Winkel. Es gilt also α+α'=90°. Wie kannst du herausfinden, wie groß α ist?

Tipp 2

γ und γ' sind Nebenwinkel. Es gilt also γ+γ'=180°. Wie kannst du herausfinden, wie groß γ' ist?

Tipp 3

Berechne den fehlenden Winkel β mithilfe des Innenwinkelsatzes!

Lösung

Aufgabe 2.3

Bestimme die Innenwinkel des Dreiecks!

Tipp 1

α und α' sind Stufenwinkel. Wie groß ist dann α'?

Tipp 2

β und β' sind Scheitelwinkel. Wie groß ist dann β?

Tipp 3

Berechne den fehlenden Winkel γ mithilfe des Innenwinkelsatzes!

Lösung

Aufgabe 4 (Sicherung)

Hier kommst du zurück zur Startseite des Kapitels: Geometrie im Dreieck