Janne Uni MS-13/Testseite: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
(Sichern meiner Sachen vom Projekt DiWers) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 110: | Zeile 110: | ||
{{Lösung versteckt|1='''a)''' 56 cm <math>\hspace{0.5cm}</math> '''b)''' 160 km<math>\hspace{0.5cm}</math> '''c)''' 108 l<math>\hspace{0.5cm}</math> '''d)''' 20 min<math>\hspace{0.5cm}</math> |2=Lösung anzeigen| | {{Lösung versteckt|1='''a)''' 56 cm <math>\hspace{0.5cm}</math> '''b)''' 160 km<math>\hspace{0.5cm}</math> '''c)''' 108 l<math>\hspace{0.5cm}</math> '''d)''' 20 min<math>\hspace{0.5cm}</math> |2=Lösung anzeigen| | ||
3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
Aktuell: | |||
==Brüche und Anteile== | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] | |||
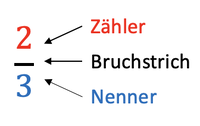
Merksatz: Brüche als Anteil eines Ganzen|Brüche sind Teile eines Ganzen. Der '''Nenner''' gibt an, in wie viele gleich große Teile das Ganze aufgeteilt wurde. Der '''Zähler''' gibt an, um wie viele Teile des Ganzen es geht. Man spricht: "Zwei Drittel". | |||
[[Datei:Bildschirmfoto 2024-05-04 um 12.09.08.png|rahmenlos|200x200px]] | |||
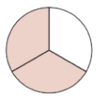
Der ganze Kreis wurde in 3 gleich große Teile aufgeteilt. 2 Teile des Ganzen sind rot markiert. | |||
[[Datei:Bildschirmfoto 2024-05-04 um 13.28.23.png|rahmenlos|100x100px]]|Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|(*)Aufgabe: 1: Brüche und Anteile zuordnen|Ordne die Brüche den passenden Darstellungen zu.{{LearningApp|width=100%|height=500px|app=35838343}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |||
(*)Aufgabe: 2: Brüche benennen|Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen: | |||
Benenne die einzelnen Brüche. | |||
'''Beispiel:''' <math> \frac{1}{4} </math> ein Viertel | |||
'''a)'''<math> \frac{1}{8} </math> <math>\hspace{0.5cm}</math> '''b)'''<math> \frac{2}{6} </math> <math>\hspace{0.5cm}</math> '''c)'''<math> \frac{1}{3} </math> <math>\hspace{0.5cm}</math> '''d)'''<math> \frac{1}{6} </math> <math>\hspace{0.5cm}</math> | |||
{{Lösung versteckt|1= | |||
'''a)''' Ein Achtel<math>\hspace{0.5cm}</math> '''b)''' Zwei Sechstel<math>\hspace{0.5cm}</math> '''c)''' Ein Drittel<math>\hspace{0.5cm}</math> '''d)''' Ein Sechstel<math>\hspace{0.5cm}</math> | |||
|2=Lösung anzeigen|3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
{{Box|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |||
(*)Aufgabe: 3: Anteile benennen|Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen: | |||
Gib die jeweiligen Anteile an. | |||
'''a)''' Fünf Kinder einer Klasse mit 28 Schülerinnen und Schülern sind muslimisch. | |||
'''b)''' Am Wandertag hat die Klasse bei der Rast schon 4km von 9km zurückgelegt. | |||
'''c)''' Von 27 Schülerinnen und Schülern in der Klasse haben 5 die Hausaufgaben nicht gemacht. | |||
'''d)''' Mathe ist das Lieblingsfach bei 11 von 24 Schülerinnen und Schülern. | |||
{{Lösung versteckt|1= | |||
'''a)'''<math> \frac{5}{28} </math> <math>\hspace{0.5cm}</math> '''b)'''<math> \frac{4}{9} </math> <math>\hspace{0.5cm}</math> '''c)'''<math> \frac{5}{27} </math> <math>\hspace{0.5cm}</math> '''d)'''<math> \frac{11}{24} </math> <math>\hspace{0.5cm}</math> | |||
|2=Lösung anzeigen|3=Lösung verstecken}}|Arbeitsmethode | |||
| Farbe = {{Farbe|orange}} | |||
}} | |||
==Bruchteile von Größen== | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] | |||
Merksatz: Bruchteile von Größen|Der Bruchteil einer Größe beschreibt einen bestimmten Anteil von einer Größe wie Meter, Kilogramm oder Euro. | |||
Um einen Bruchteil einer Größe zu berechnen, musst du | |||
1. durch den Nenner teilen | |||
2. mit dem Zähler multiplizieren. | |||
Manchmal musst du auch zuerst in eine kleinere Einheit umrechnen, also beispielsweise Meter in Zentimeter oder Stunden in Minuten umwandeln.| Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
{{Box|Beispiel: Bruchteile von Größen|Bestimme <math> \frac{3}{4} </math> von 16 Bananen. | |||
<math> 16 : 4 = 4 </math>, also sind 4 Bananen <math> \frac {1}{4} </math> von 16 Bananen. | |||
<math> 4 \cdot 3 = 12 </math>, also sind 12 Bananen <math> \frac {3}{4} </math> von 16 Bananen. | |||
Wir unterteilen also die 16 Bananen in 4-er-Päckchen und nehmen dann 3 dieser 4-er-Päckchen. | |||
[[Datei:Bildschirmfoto 2024-05-23 um 14.02.29.png|rahmenlos|200x200px]] | |||
|Hervorhebung1 | |||
}} | |||
Probiere es doch gleich mal aus! | |||
{{Box|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] | |||
(*)Aufgabe 4: Bruchteile von Größen bestimmen|Notiere auf deinem Arbeitsblatt und vergleiche deine Ergebnisse danach mithilfe der Lösungen: | |||
Berechne die Anteile. Wandle, wenn nötig, vorher in eine kleinere Einheit um. | |||
'''a)''' <math>\frac{2}{7}</math> von 56 cm <math>\hspace{1cm} </math> | |||
'''b)''' <math>\frac{4}{9}</math> von 54 min <math>\hspace{1cm} </math> | |||
'''c)''' <math>\frac{2}{5}</math> von 1€ <math>\hspace{1cm} </math> | |||
'''d)''' Maja hat drei Viertel ihrer 28 km langen Radstrecke zurückgelegt. Berechne, wie weit sie schon gefahren ist. | |||
'''e)''' Cem braucht zum Backen <math>\frac{3}{8}</math> von einem Kilogramm Butter. Berechne, wie viel Gramm er abwiegen muss. | |||
{{Lösung versteckt|1= Denk daran, dass 1€ = 100 Cent, 1kg = 1000g und 1km = 1000m entspricht.|2= Tipp anzeigen|3= Tipp verstecken}} | |||
{{Lösung versteckt|1='''a)''' 16 cm <math>\hspace{0.5cm}</math> '''b)''' 24 min<math>\hspace{0.5cm}</math> '''c)''' 40 Cent<math>\hspace{0.5cm}</math> '''d)''' 21 km <math>\hspace{0.5cm}</math> '''e)''' 375 g <math>\hspace{0.5cm}</math> |2=Lösung anzeigen| | |||
3=Lösung verstecken}}|Arbeitsmethode | 3=Lösung verstecken}}|Arbeitsmethode | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
Aktuelle Version vom 23. Mai 2024, 12:41 Uhr
Probiere es doch gleich mal aus!
Aktuell:
Brüche und Anteile
Bruchteile von Größen
Probiere es doch gleich mal aus!