|
|
| Zeile 154: |
Zeile 154: |
|
| |
|
| {{Box | [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](***)| '''c)''' Wie groß könnte der Durchschnitt bei einem Median von 3 Toren maximal werden? Überleg dir warum es manchmal sinnvoller sein könnte den Median anzugeben, als den Durchschnitt und umgekehrt. | Arbeitsmethode}} | | {{Box | [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](***)| '''c)''' Wie groß könnte der Durchschnitt bei einem Median von 3 Toren maximal werden? Überleg dir warum es manchmal sinnvoller sein könnte den Median anzugeben, als den Durchschnitt und umgekehrt. | Arbeitsmethode}} |
|
| |
| ===Median===
| |
| {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Der '''Median''' wird auch '''Zentralwert''' genannt. Der Median bezeichnet das Ergebnis, das wenn du nach Häufigkeiten sortierst, in der Mitte liegt. Wenn die Anzahl der Möglichkeiten grade ist, liegen zwei Werte in der Mitte, dann musst du den Durchschnitt dieser beiden Werte ausrechnen.|Merksatz
| |
| | Farbe = {{Farbe|grün}}
| |
| }}
| |
| {{Box|Beispiel Geburtstagskalender|Um den Median zu bestimmen, werden alle Werte der Größe nach sortiert: <math>0,0,1,1,1,2,2,2,3,3,4,6</math>. Da wir eine gerade Anzahl an Ergebnissen haben, müssen wir den Durchschnitt der beiden mittleren Ergebnisse bestimmen, also <math>\frac{2+2}{2}=2</math>.|Hervorhebung1
| |
| }}
| |
|
| |
| {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 3.3 (*): Fußballturnier|'''a)'''{{LearningApp|width=100%|height=500px|app=pfdmx16ic24}}
| |
|
| |
| {{LearningApp|width=100%|height=500px|app=pb3wizu9j24}}|Arbeitsmethode
| |
| | Farbe = {{Farbe|orange}}}}
| |
|
| |
| [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt'''
| |
|
| |
| {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](**)|'''b)''' Was fällt dir auf, wenn du die einzelnen statistischen Kenngrößen von Jasmin und Luca vergleichst? |Arbeitsmethode | Farbe = #CD2990}}
| |
|
| |
| {{Box | [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]](***)| '''c)''' Theo hat in den 5 Spielen auch 3 Tore im Durchschnitt geschossen, er sagt, er hat einen Median von 5 Toren. Überlege wie viele Tore Theo in welchem Spiel geschossen haben könnte, damit die Angaben stimmen. Bestimme anschließend auch Minimum, Maximum und Spannweite. | Arbeitsmethode}}
| |
|
| |
|
| ==Zuordnungen & Weg-Zeit-Diagramme== | | ==Zuordnungen & Weg-Zeit-Diagramme== |
Version vom 13. Mai 2024, 18:42 Uhr
Info
In diesem Lernpfadkapitel wiederholen wir mit dir den Umgang mit Daten, negativen Zahlen und Zuordnungen.
In diesem Kapitel wirst du,
- ...
- ...
- ...
- Zuordnungen in Form von Weg-Zeit-Diagrammen erneut kennenlernen.
- Weg-Zeit-Diagramme lesen sowie erstellen.
- Weg-Zeit-Diagramme miteinander vergleichen.
- Weg-Zeit-Diagramme mit realen Situationen vergleichen und zuordnen.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
- Bei einigen Aufgaben findest du oben links ein kleines Fragezeichen oder eine Glühlampe. Wenn du die Aufgabenstellung nochmal lesen möchtest, klicke auf das Fragezeichen. Wenn du einen Tipp brauchst, klicke auf die Glühlampe.
Viel Spaß!
Zahlen
Zahlenstrahl
Egal wie fein man die Einteilung für einen Zahlenstrahl wählt, es ist immer möglich eine noch feinere Einteilung zu finden.
Beispiel Zahlenstrahl
An dieser Abbildung erkennst du sehr anschaulich, dass die Einteilung des Zahlenstrahles immer feiner wird.
Aufgabe 1.1 (*): Welche Zahl ist am Zahlenstrahl markiert? Zahlen ablesen und benennen
Negative Zahlen
An einem Zahlenstrahl kommen natürlich auch die negativen Zahlen vor, diese kann man auch addieren und subtrahieren.
Beispiel Zahlenstrahl mit negativen Zahlen
Aufgabe 1.2 (*): Addieren und Subtrahieren mit negativen Zahlen
Ordnen von ganzen Zahlen
An einem Zahlenstrahl gilt:
- Nach links werden die Zahlen kleiner
- Nach
rechts werden die Zahlen
größer
Merksatz: Ordnen von ganzen Zahlen
Vervollständige den Merksatz.
An einem Zahlenstrahl gilt:
- Nach links werden die Zahlen kleiner
- Nach rechts werden die Zahlen größer
Runden von ganzen Zahlen
Manchmal kann man Zahlen nicht genau darstellen, dann wird gerundet.
Merksatz: Runden von Zahlen
1. Finde die Rundungsstelle (z.B. runde auf Hunderter oder Zehner)
2. Schau nach, welche Ziffer hinter der Rundungsstelle steht.
Vervollständige den Merksatz.
Ist die erste Ziffer, die hinter der Rundungsstelle steht, eine 0; 1; 2; 3 oder 4, so wird abgerundet.
Ist die erste Ziffer, die hinter der Rundungsstelle steht, eine, 5; 6; 7; 8 oder 9, so wird aufgerundet.
Daten erheben & darstellen
Daten können auf verschiedene Arten dargestellt werden. Du kennst bereits Strichlisten, Häufigkeitstabellen, Säulendiagramme und Kreisdiagramme. Je nach Situation eignet sich oft eine Darstellungsform am meisten.
Aufgabe 2.1 (*): Wie heißt das? Diagramme benennen und Informationen ablesen
Aufgabe 2.2 (**)
a) Bearbeite die Learningapp!
b) Begründe auf dem AB, warum die anderen Diagramme nicht infrage kamen!
Aufgabe 2.3 (***): Lieblings- und Haustiere der 6c
Statistische Kenngrößen
Häufigkeiten
Es gibt zwei verschiedene Arten, wie Häufigkeiten gemessen und verglichen werden: Die absolute Häufigkeit und die relative Häufigkeit.
absolute Häufigkeit
Die absolute Häufigkeit ist die Anzahl, wie oft etwas vorkommt. Du kannst sie zum Beispiel mit Hilfe einer Strichliste zählen.
relative Häufigkeit
Die relative Häufigkeit ist der Anteil von der Gesamtzahl. Dafür wird die absolute Häufigkeit durch die Gesamtzahl dividiert. Die relative Häufigkeit kann als Bruch, Dezimalzahl oder Prozentzahl angegeben werden.
Aufgabe 3.1 (*) : Umrechnen von relativen Häufigkeiten
Aufgabe 3.2 (*) : Geburtstagskalender
Du kannst die Aufgabe nach dem Starten oben links nochmal anzeigen lassen.
Maximum, Minimum und Spannweite
Der kleinste Wert in den Antworten heißt Minimum. Der größte Wert heißt Maximum. Wenn du das Minimum vom Maximum abziehst, erhältst du die Spannweite.
Beispiel Geburtstagskalender
Minimum: Im März und Oktober hat niemand aus der Klasse Geburtstag, deshalb ist das Minimum 0.
Maximum: Im Juli haben am meisten Kinder Geburtstag, nämlich 6. Also ist 6 das Maximum.
Spannweite: Für die Spannweite ziehst du das Minimum vom Maximum ab, also

.
Median
Der Median wird auch Zentralwert genannt. Der Median bezeichnet das Ergebnis, das wenn du nach Häufigkeiten sortierst, in der Mitte liegt. Wenn die Anzahl der Möglichkeiten grade ist, liegen zwei Werte in der Mitte, dann musst du den Durchschnitt dieser beiden Werte ausrechnen.
Beispiel Geburtstagskalender
Um den Median zu bestimmen, werden alle Werte der Größe nach sortiert:

. Da wir eine gerade Anzahl an Ergebnissen haben, müssen wir den Durchschnitt der beiden mittleren Ergebnisse bestimmen, also

.
Aufgabe 3.3 (*): Fußballturnier
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt
b) Theo hat in den 5 Spielen auch 3 Tore im Durchschnitt geschossen, er sagt, er hat in einem Spiel 9 Tore geschossen und einen Median von 3 Toren. Überlege wie viele Tore Theo in welchem Spiel geschossen haben könnte, damit die Angaben stimmen.
c) Wie groß könnte der Durchschnitt bei einem Median von 3 Toren maximal werden? Überleg dir warum es manchmal sinnvoller sein könnte den Median anzugeben, als den Durchschnitt und umgekehrt.
Zuordnungen & Weg-Zeit-Diagramme
Einführung - Was ist eine Zuordnung?
Beispiel: Streckenmessung beim Joggen
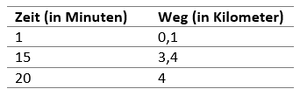
In der Tabelle wird jeweils einem Messzeitpunkt (angegeben in Minuten) eine bereits zurückgelegte Strecke (in Kilometer) zugeordnet.
Zuordnungen findest du überall in deinem Alltag. Oft können sie in Tabellen dargestellt werden, wobei einem Tabellenwert in der linken Spalte genau ein Tabellenwert in der rechten Spalte zugewiesen wird.
Die Tabelle rechts gibt zum Beispiel die Laufzeiten eines Schülers beim Joggen im Sportunterricht an. Hierbei wird einem Zeitpunkt immer genau eine Meteranzahl zugeordnet.
Zuordnungen wie die obige lassen sich auch in einem Koordinatensystem einzeichnen. Wir erhalten dann ein Weg-Zeit-Diagramm.

Das Weg-Zeit-Diagramm stellt die Daten aus der bereits betrachteten Tabelle in einem Koordinatensystem dar und lässt auch Vermutungen über die zurückgelegte Strecke nach nicht gemessenen Zeitpunkten zu.
Merksatz: Zuordnungen im Weg-Zeit-Diagramm
Zu jedem Zeitpunkt gibt es immer nur eine Strecke die zugeordnet werden kann, eine Streckenzahl kann aber mehreren Zeitpunkten zugeordnet werden!
Weg-Zeit-Diagramme lesen & konstruieren
Aufgabe 4.1(*): Weg-Zeit-Diagramme lesen
Die Klasse 5C plant am Wandertag mit einem Bus zum nähst gelegenen Stausee zu fahren. Während der Fahrt messen sie in regelmäßigen Abständen wie viele Kilometer sie bereits gefahren sind und fertigen anhand dieser Daten ein Weg-Zeit-Diagramm an. Im Anschluss an den Wandertag hat die Klassenlehrerin Frau Müller ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten?
Fragen zu Aufgabe 4.1(*): Weg-Zeit-Diagramme lesen
Wie viel km hat der Bus nach 5 Minuten zurückgelegt? 8()
Nach wie vielen Minuten hat der Bus etwa 10km zurückgelegt? 6()
Wie viel km hat der Bus nach 18min zurückgelegt? 14()
Etwa 3km hat der Bus nach wie vielen Minuten zurückgelegt? 2()
Aufgabe 4.2(*): Weg-Zeit-Diagramme konstruieren
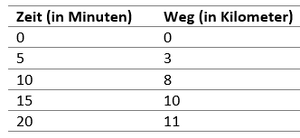
Die zurückgelegte Strecke (in Kilometer) abhängig von der bereits gefahrenen Zeit (in Minuten).
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt
Die Klasse 5A hatte bei ihrem Wandertag eine ähnliche Idee und hat während ihrer Busfahrt auch regelmäßig die Abstände in Kilometern gemessen. Als Ergebnis erhielten sie folgende Tabelle.
Kannst du mithilfe der Tabelle ein Weg-Zeit-Diagramm auf deinem Arbeitsblatt erstellen? Zeichne dazu zunächst ein geeignetes Koordinatensystem und erstelle dann das Weg-Zeit-Diagramm.
Hinweis: In der folgenden
Tipp Box findest du ein Applet um nachzuvollziehen wie aus einer Zuordnung in einer Tabelle ein Weg-Zeit-Diagramm wird, vielleicht hilft es dir ja bei der Bearbeitung der Aufgabe.
Von der Tabelle zum Graphen
Führe die folgenden Schritte 1 bis 8 aus, um zu beobachten wie aus einer Zuordnungstabelle ein Graph im Koordinatensystem werden kann.
Weg-Zeit-Diagramme - Zusammenhänge herstellen
Aufgabe 4.3(**): Weg-Zeit-Diagramme vergleichen
Da der Ausflug der Klasse 5C zum Stausee ein voller Erfolg war, entschließt sich die Klasse 5D im folgenden Jahr ebenfalls zum Stausee zu fahren. Der Busfahrer der 5D im roten Bus nimmt jedoch einen anderen Weg zum Stausee. Glücklicherweise misst auch die 5D in regelmäßigen Abständen die bereits zurückgelegte Strecke und ergänzt diese im Weg-Zeit-Diagramm. Im Anschluss an die Fahrt an den Stausee Frau Müller erneut ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten?
Fragen zu Aufgabe 4.3(**): Weg-Zeit-Diagramme vergleichen
Wie viel Kilometer liegt der rote Bus hinter dem blauen Bus nach 6min? 6()
Welche Farbe hat der Bus, welcher nach 2 Minuten die größere Strecke zurückgelegt hat? blau()
Wie viel Kilometer haben die Busse nach 18 Minuten jeweils zurückgelegt? 14()
Welcher Farbe hat der Bus, welcher in den ersten 6 Minuten am langsamsten fuhr? Der rot()
Weg-Zeit-Diagramme im Sachkontext
Aufgabe 4.4(***): Weg-Zeit-Diagramme zuordnen
Ordne die Weg-Zeit-Diagramme einem passenden Sachkontext, also einer passenden Beschreibung einer realen Situation, zu.








