Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Zuordnungen, Zahlen und Daten: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung |
||
| Zeile 49: | Zeile 49: | ||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
}} | }} | ||
{{Box | |||
| 1 = [[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]Merksatz: Runden und Überschlage bei Dezimalzahlen | |||
| 2 = Vor dem '''Runden''' von Dezimalzahlen muss du festlegen, wie viele Stellen nach dem Komma die gerundete Zahl haben soll. | |||
Vervollständige den Merksatz. | |||
<div class="lueckentext-quiz"> | |||
Ist die erste Ziffer, die du weglässt, 0; 1; 2; 3 oder 4, so wird '''abgerundet'''. | |||
Ist die erste Ziffer, die du weglässt, 5; 6; 7; 8 oder 9, so wird '''aufgerundet'''. | |||
</div> | |||
''Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt.'' | |||
| 3 = Merksatz | |||
| Farbe = {{Farbe|grün|dunkel}} | |||
}} | |||
== Daten erheben & darstellen== | |||
==Daten erheben & darstellen== | |||
Daten können auf verschiedene Arten dargestellt werden. Du kennst bereits '''Strichlisten''', '''Häufigkeitstabellen''', '''Säulendiagramme''' und '''Kreisdiagramme'''. Je nach Situation eignet sich oft eine Darstellungsform am meisten. | Daten können auf verschiedene Arten dargestellt werden. Du kennst bereits '''Strichlisten''', '''Häufigkeitstabellen''', '''Säulendiagramme''' und '''Kreisdiagramme'''. Je nach Situation eignet sich oft eine Darstellungsform am meisten. | ||
| Zeile 83: | Zeile 98: | ||
}} | }} | ||
====relative Häufigkeit ==== | ====relative Häufigkeit==== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Die '''relative Häufigkeit''' ist der Anteil von der Gesamtzahl. Dafür wird die absolute Häufigkeit durch die Gesamtzahl dividiert. Die relative Häufigkeit kann als Bruch, Dezimalzahl oder Prozentzahl angegeben werden.|Merksatz | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Die '''relative Häufigkeit''' ist der Anteil von der Gesamtzahl. Dafür wird die absolute Häufigkeit durch die Gesamtzahl dividiert. Die relative Häufigkeit kann als Bruch, Dezimalzahl oder Prozentzahl angegeben werden.|Merksatz | ||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 3.1 | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 3.1: Umrechnen von relativen Häufigkeiten|{{LearningApp|width=100%|height=500px|app=19569399}}|Arbeitsmethode | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 3.2 | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 3.2: Geburtstagskalender|{{LearningApp|width=100%|height=500px|app=pzs1nja7k24}}|Arbeitsmethode | ||
| Farbe = {{Farbe|orange}} | | Farbe = {{Farbe|orange}} | ||
}} | }} | ||
| Zeile 108: | Zeile 123: | ||
}} | }} | ||
===Durchschnitt=== | ===Durchschnitt === | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Den '''Durchschnitt''' nennt man auch '''arithmetisches Mittel'''. Um ihn zu berechnen, addiert man alle absoluten Häufigkeiten und dividiert diese durch die Anzahl der Möglichkeiten.|Merksatz | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Den '''Durchschnitt''' nennt man auch '''arithmetisches Mittel'''. Um ihn zu berechnen, addiert man alle absoluten Häufigkeiten und dividiert diese durch die Anzahl der Möglichkeiten.|Merksatz | ||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
| Zeile 116: | Zeile 131: | ||
}} | }} | ||
=== Median=== | ===Median=== | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Der '''Median''' wird auch '''Zentralwert''' genannt. Der Median bezeichnet das Ergebnis, das wenn du nach Häufigkeiten sortierst, in der Mitte liegt. Wenn die Anzahl der Möglichkeiten grade ist, liegen zwei Werte in der Mitte, dann musst du den Durchschnitt dieser beiden Werte ausrechnen.|Merksatz | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]]|Der '''Median''' wird auch '''Zentralwert''' genannt. Der Median bezeichnet das Ergebnis, das wenn du nach Häufigkeiten sortierst, in der Mitte liegt. Wenn die Anzahl der Möglichkeiten grade ist, liegen zwei Werte in der Mitte, dann musst du den Durchschnitt dieser beiden Werte ausrechnen.|Merksatz | ||
| Farbe = {{Farbe|grün}} | | Farbe = {{Farbe|grün}} | ||
| Zeile 123: | Zeile 138: | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 3.3 | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] Aufgabe 3.3: Fußballturnier|'''a)'''{{LearningApp|width=100%|height=500px|app=pfdmx16ic24}} | ||
{{LearningApp|width=100%|height=500px|app=pb3wizu9j24}}|Arbeitsmethode | {{LearningApp|width=100%|height=500px|app=pb3wizu9j24}}|Arbeitsmethode | ||
| Zeile 129: | Zeile 144: | ||
}} | }} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] '''b)''' | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]|'''b)''' Was fällt dir auf, wenn du die einzelnen statistischen Kenngrößen von Jasmin und Luca vergleichst? | ||
'''c)''' Warum unterscheidet sich der Median, der Durchschnitt jedoch nicht?|Arbeitsmethode | |||
| Farbe = #CD2990 | | Farbe = #CD2990 | ||
}} | |||
==Zuordnungen & Weg-Zeit-Diagramme== | ==Zuordnungen & Weg-Zeit-Diagramme== | ||
| Zeile 155: | Zeile 168: | ||
}} | }} | ||
=== Weg-Zeit-Diagramme lesen & konstruieren=== | ===Weg-Zeit-Diagramme lesen & konstruieren=== | ||
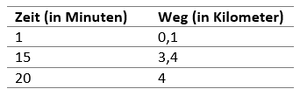
{{Box|Aufgabe 4.1(*): Weg-Zeit-Diagramme lesen|Die Klasse 5C plant am Wandertag mit einem Bus zum nähst gelegenen Stausee zu fahren. Während der Fahrt messen sie in regelmäßigen Abständen wie viele Kilometer sie bereits gefahren sind und fertigen anhand dieser Daten ein Weg-Zeit-Diagramm an. Im Anschluss an den Wandertag hat die Klassenlehrerin Frau Müller ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten? | {{Box|Aufgabe 4.1(*): Weg-Zeit-Diagramme lesen|Die Klasse 5C plant am Wandertag mit einem Bus zum nähst gelegenen Stausee zu fahren. Während der Fahrt messen sie in regelmäßigen Abständen wie viele Kilometer sie bereits gefahren sind und fertigen anhand dieser Daten ein Weg-Zeit-Diagramm an. Im Anschluss an den Wandertag hat die Klassenlehrerin Frau Müller ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten? | ||
| Zeile 196: | Zeile 209: | ||
3=Tipp verbergen}} | 3=Tipp verbergen}} | ||
===Weg-Zeit-Diagramme - Zusammenhänge herstellen === | ===Weg-Zeit-Diagramme - Zusammenhänge herstellen=== | ||
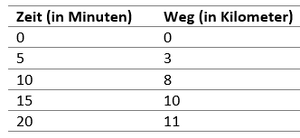
{{Box|Aufgabe 4.3(**): Weg-Zeit-Diagramme vergleichen|Da der Ausflug der Klasse 5C zum Stausee ein voller Erfolg war, entschließt sich die Klasse 5D im folgenden Jahr ebenfalls zum Stausee zu fahren. Der Busfahrer der 5D im roten Bus nimmt jedoch einen anderen Weg zum Stausee. Glücklicherweise misst auch die 5D in regelmäßigen Abständen die bereits zurückgelegte Strecke und ergänzt diese im Weg-Zeit-Diagramm. Im Anschluss an die Fahrt an den Stausee Frau Müller erneut ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten? | {{Box|Aufgabe 4.3(**): Weg-Zeit-Diagramme vergleichen|Da der Ausflug der Klasse 5C zum Stausee ein voller Erfolg war, entschließt sich die Klasse 5D im folgenden Jahr ebenfalls zum Stausee zu fahren. Der Busfahrer der 5D im roten Bus nimmt jedoch einen anderen Weg zum Stausee. Glücklicherweise misst auch die 5D in regelmäßigen Abständen die bereits zurückgelegte Strecke und ergänzt diese im Weg-Zeit-Diagramm. Im Anschluss an die Fahrt an den Stausee Frau Müller erneut ein paar Fragen an die Klasse, kannst du die Fragen mithilfe des Weg-Zeit-Diagramms beantworten? | ||
Version vom 13. Mai 2024, 16:35 Uhr
Zahlen
Zahlenstrahl

negative Zahlen
runden von Zahlen
Manchmal kann man Zahlen nicht genau darstellen, dann wird gerundet.
Daten erheben & darstellen
Daten können auf verschiedene Arten dargestellt werden. Du kennst bereits Strichlisten, Häufigkeitstabellen, Säulendiagramme und Kreisdiagramme. Je nach Situation eignet sich oft eine Darstellungsform am meisten.
Aufgabe 2.2 (**)
a) Bearbeite die Learningapp!
b) Begründe auf dem AB, warum die anderen Diagramme nicht infrage kamen!
Statistische Kenngrößen
Häufigkeiten
Es gibt zwei verschiedene Arten, wie Häufigkeiten gemessen und verglichen werden: Die absolute Häufigkeit und die relative Häufigkeit.
absolute Häufigkeit
relative Häufigkeit
Maximum, Minimum und Spannweite
Durchschnitt
Median
Zuordnungen & Weg-Zeit-Diagramme
Einführung - Was ist eine Zuordnung?
Weg-Zeit-Diagramme lesen & konstruieren
Fragen zu Aufgabe 4.1(*): Weg-Zeit-Diagramme lesen
Wie viel km hat der Bus nach 5 Minuten zurückgelegt? 8()
Nach wie vielen Minuten hat der Bus etwa 10km zurückgelegt? 6()
Wie viel km hat der Bus nach 18min zurückgelegt? 14()
Etwa 3km hat der Bus nach wie vielen Minuten zurückgelegt? 2()
Von der Tabelle zum Graphen
Führe die folgenden Schritte 1 bis 8 aus, um zu beobachten wie aus einer Zuordnungstabelle ein Graph im Koordinatensystem werden kann.

Weg-Zeit-Diagramme - Zusammenhänge herstellen
Fragen zu Aufgabe 4.3(**): Weg-Zeit-Diagramme vergleichen
Wie viel Kilometer liegt der rote Bus hinter dem blauen Bus nach 6min? 6()
Welche Farbe hat der Bus, welcher nach 2 Minuten die größere Strecke zurückgelegt hat? blau()
Wie viel Kilometer haben die Busse nach 18 Minuten jeweils zurückgelegt? 14()
Welcher Farbe hat der Bus, welcher in den ersten 6 Minuten am langsamsten fuhr? Der rot()