Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Geometrische Figuren und Winkel/Geraden, Strecken, Parallelen und Senkrechten: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 8: | Zeile 8: | ||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz| | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz| | ||
Eine '''Gerade''' ist eine gerade Linie, die durch mehrere Punkte gehen kann. Sie hat weder Start- noch Endpunkt, ist also unendlich, und kann deshalb nie vollständig gezeichnet werden. Sie wird mit kleinen Buchstaben, wie g oder h bezeichnet. | Eine '''Gerade''' ist eine gerade Linie, die durch mehrere Punkte gehen kann. Sie hat weder Start- noch Endpunkt, ist also unendlich, und kann deshalb nie vollständig gezeichnet werden. Sie wird mit kleinen Buchstaben, wie g oder h bezeichnet. | ||
Eine Strecke ist eine gerade Linie, die zwischen zwei Punkten verläuft. Sie hat also einen Startpunkt und einen Endpunkt und kann also vollständig gezeichnet werden. Sie wird mit <math>\overline{AB}</math> oder <math>\overline{CD}</math> usw. bezeichnet.|Merksatz}} | Eine '''Strecke''' ist eine gerade Linie, die zwischen zwei Punkten verläuft. Sie hat also einen Startpunkt und einen Endpunkt und kann also vollständig gezeichnet werden. Sie wird mit <math>\overline{AB}</math> oder <math>\overline{CD}</math> usw. bezeichnet.|Merksatz}} | ||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 2: Eigenschaften von Senkrechten und Orthogonalen und Strecken|Fülle den Lückentext aus! | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]] (*) Aufgabe 2: Eigenschaften von Senkrechten und Orthogonalen und Strecken|Fülle den Lückentext aus! | ||
Version vom 12. Mai 2024, 12:42 Uhr
Geraden, Strecken, Parallelen und Senkrechten
Setze die Wörter an den passenden Stellen ein.
Die Aufgabe lautet: "Stelle den Anteil grafisch dar." Was musst du dann tun?
Erinnere dich: Unten im Bruch steht die Gesamtzahl der Kästchen. Man nennt diese Zahl auch Nenner.
Oben steht die Anzahl der gefärbten Kästchen.
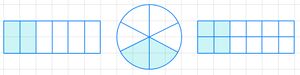
Du zeichnest also zum Beispiel drei gleich große Kästchen. Davon malst du ein Kästchen farbig aus.
Du kannst auch einen Kreis zeichnen.
Teile den Kreis in drei gleich große Teile. Male davon einen Teil aus.
Du kannst den Bruch vor dem Zeichen auch erweitern:
Nun teilst du den Kreis in sechs gleich große Teile. Davon malst du zwei Teile farbig an. Du kannst den Bruch mit jeder anderen Zahl erweitern.
Beim Erweitern muss man Zähler und Nenner mit der gleichen Zahl multiplizieren.
Beim Kürzen muss man Zähler und Nenner mit der gleichen Zahl dividiert.
Zum Addieren und Subtrahieren von Brüchen müssen die Nenner gleich sein. Dann addiert bzw. subtrahiert man die Zähler.

- Wähle das erste Werkzeug "Strecke" in der Leiste aus. Klicke nun zuerst den Punkt A und dann den Punkt B an. Nun hast du die geforderte Strecke gezeichnet.
- Wähle das zweite Werkzeug "Gerade" in der Leiste aus. Klicke nun zuerst den Punkt C und dann den Punkt E an. Nun hast du die geforderte Gerade gezeichnet.
- Was musst du hier zeichnen? Eine Strecke oder eine Gerade? Wähle hierfür das entsprechende Werkzeug aus und gehe wie eben vor.
- Wähle das vierte Werkzeug "Strecke mit fester Länge" aus. Klicke zuerst den Punkt E an. Es öffnet sich ein neues Fenster u nd du musst du die gewünschte Länge deiner Strecke eingeben; hier: 3. Achtung: Du darfst die Einheit cm nicht mit eintippen. Bestätige die Eingabe mit "OK" und die Strecke wird gezeichnet. Geogebra erstellt für das Ende der Strecke den Punkt F.