Digitale Werkzeuge in der Schule/Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6/Flächen und Körper/Umfang berechnen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Kleine Lernstandserhebung zur Doppeljahrgangsstufe 5/6 | Flächen und Körper
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== Umfang berechnen == | == Umfang berechnen == | ||
Auf dieser Seite wiederholen wir, wie man den Umfang von Vierecken berechnet. | Auf dieser Seite wiederholen wir, wie man den Umfang von Vierecken berechnet. Sobald du die Formel herausgefunden und verstanden hast, schreibe sie einmal in dein "Regelheft". | ||
<ggb_applet id="wdgpkuca" width="800" height="580" border="888888" /> | <ggb_applet id="wdgpkuca" width="800" height="580" border="888888" /> | ||
| Zeile 6: | Zeile 6: | ||
In einer Box: Wenn du herausgefunden hast, wie man den Umfang von einem Rechteck berechnen kann, schreibe dir die Lösung auf dem Arbeitsblatt auf. | In einer Box: Wenn du herausgefunden hast, wie man den Umfang von einem Rechteck berechnen kann, schreibe dir die Lösung auf dem Arbeitsblatt auf. | ||
{{Box|1=Umfang des Rechtecks|2=[[Datei:Umfang Rechteck.jpg|rahmenlos|rechts]] | {{Box | ||
| 1 = Umfang des Rechtecks | |||
| 2 = [[Datei:Umfang Rechteck.jpg|rahmenlos|rechts]] Man läuft dr<span style="color:red">UM</span> her<span style="color:red">UM</span>!<br> | |||
'''<big><u>Rechteck</u></big>'''<br> | '''<big><u>Rechteck</u></big>'''<br> | ||
<big>u = a + b + a + b<br> | <big>u = a + b + a + b<br> | ||
= 2·a + 2·b<br> | = 2·a + 2·b<br> | ||
= 2·(a + b)</big><br>|3=Arbeitsmethode}} | = 2·(a + b)</big><br> | ||
| 3 = Arbeitsmethode | |||
}} | |||
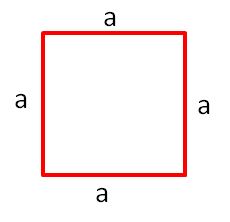
{{Box|1=Umfang des Quadrates|2=[[Datei:Umfang Quadrat.jpg|rechts|rahmenlos]]<br> | {{Box|1=Umfang des Quadrates|2=[[Datei:Umfang Quadrat.jpg|rechts|rahmenlos]]<br> | ||
Version vom 9. Mai 2024, 14:32 Uhr
Umfang berechnen
Auf dieser Seite wiederholen wir, wie man den Umfang von Vierecken berechnet. Sobald du die Formel herausgefunden und verstanden hast, schreibe sie einmal in dein "Regelheft".

In einer Box: Wenn du herausgefunden hast, wie man den Umfang von einem Rechteck berechnen kann, schreibe dir die Lösung auf dem Arbeitsblatt auf.
In einer Box: Wenn du herausgefunden hast, wie man den Umfang von einem Rechteck berechnen kann, schreibe dir die Lösung auf dem Arbeitsblatt auf.
Aufgaben zum Üben
- Braucht man den Umfang oder nicht?

- Umfang von zusammengesetzten Flächen berechnen