Abitur Physik am Gymnasium Trittau/Interferenz an dünnen Schichten: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
GT060 (Diskussion | Beiträge) (Quellen) |
(Verbessert bzgl Brechungsindex) |
||
| Zeile 3: | Zeile 3: | ||
=== Berechnung === | === Berechnung === | ||
[[Datei:Brechnung an dünnen schichten.png|mini]]Die Formel für | [[Datei:Brechnung an dünnen schichten.png|mini]]Die Formel für den Gangunterschied lautet: | ||
<math>\Delta s = 2 \cdot d \cdot \sqrt{ n^2 \cdot sin^2(\alpha)}</math> | <math>\Delta s = 2 \cdot d \cdot \sqrt{ n^2 \cdot sin^2(\alpha)}</math> | ||
Dabei steht n für den Brechungsindex | Dabei steht n für den Brechungsindex.. | ||
Bei Reflektion einer tiefer liegenden Schicht (B) mit Brechungsindex n' gilt allerdings: | Bei Reflektion an einer tiefer liegenden Schicht (B) mit Brechungsindex n' > n gilt allerdings: | ||
<math>\Delta s = 2 \cdot d \cdot \sqrt{ n^2 \cdot sin^2(\alpha)} - \frac{\lambda}{2}</math> | <math>\Delta s = 2 \cdot d \cdot \sqrt{ n^2 \cdot sin^2(\alpha)} - \frac{\lambda}{2}</math> | ||
da | da bei Reflexion am optisch dichteren Medium immer ein Phasensprung der Größe <math>\pi</math>, also ein zusätzlicher Gangunterschied <math>\frac{\lambda}{2}</math> dazukommt. | ||
=== Quellen === | === Quellen === | ||
Aktuelle Version vom 5. März 2024, 10:48 Uhr
Erklärung
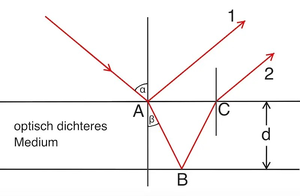
Fällt Licht auf eine dünne Schicht mit einem Brechungsindex von wird es entwieder reflektiert (Punkt A) oder dringt zum Teil in die Schicht ein und wird an einem anderen Punkt (B) reflektiert und gebrochen.
Berechnung
Die Formel für den Gangunterschied lautet:
Dabei steht n für den Brechungsindex..
Bei Reflektion an einer tiefer liegenden Schicht (B) mit Brechungsindex n' > n gilt allerdings:
da bei Reflexion am optisch dichteren Medium immer ein Phasensprung der Größe , also ein zusätzlicher Gangunterschied dazukommt.
Quellen
Formelsammlung S.131
https://www.leifiphysik.de/optik/beugung-und-interferenz/grundwissen/interferenz-duennen-schichten