Benutzer:Buss-Haskert/Vorbereitungskurs ZP 10 Mathematik/Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 189: | Zeile 189: | ||
{{Box|Nullstellen quadratischer Funktionen berechnen|Die Nullstellen sind die Schnittpunkte der Parabel mit der x-Achse, also gilt immer '''f(x) = 0'''. | {{Box|Nullstellen quadratischer Funktionen berechnen|Die Nullstellen sind die Schnittpunkte der Parabel mit der x-Achse, also gilt immer '''f(x) = 0'''. | ||
Du erhältst also immer eine quadratische Gleichung. Wie du diese löst, hast du im 1. Themenblock erarbeitet.|Merksatz}} | Du erhältst also immer eine quadratische Gleichung (rein quadratisch oder gemischt quadratisch). Wie du diese löst, hast du im 1. Themenblock erarbeitet.|Merksatz}} | ||
Beispiele: | |||
{{Box|Beispielrechnungen für Nullstellenberechnungen|Übertrage die nachfolgenden Beispiele zur Nullstellenbrechnung in dein Heft.|Arbeitsmethode}} | |||
<u><big>1. Form: f(x) = ax² </big></u><br> | |||
Beispiel: f(x) = 3x²<br> | |||
f(x) = 0<br> | |||
3x² = 0 |:3<br> | |||
x² = 0 |<math>\surd</math><br> | |||
x = 0 <br> | |||
N(0|0)<br> | |||
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle. | |||
<u><big>2. Form: f(x) = ax² + c </big></u> | |||
Beispiel: f(x) = 0,5x² - 8<br> | |||
f(x) = 0<br> | |||
0,5x² - 8 = 0 |+8<br> | |||
0,5x² = 8 |:0,5<br> | |||
x² = 16 |<math>\surd</math><br> | |||
x<sub>1</sub> = - <math>\sqrt{16}</math> und x<sub>2</sub> = + <math>\sqrt{16}</math><br> | |||
x<sub>1</sub> = -4 und x<sub>2</sub> = +4 | |||
<br> | |||
N<sub>1</sub>(-4|0) und N<sub>2</sub>(4|0)<br> | |||
<u><big>3. Form: Scheitelpunktform f(x) = a(x+d)²+e </big></u> | |||
Beispiel: f(x) = 2(x + 2)² - 18<br> | |||
[[Datei:F(x) = 2(x+2)²-18.png|rechts|rahmenlos|425x425px]] | |||
f(x) = 0<br> | |||
2(x + 2)² - 18 = 0 |+18<br> | |||
2(x + 2)² = 18 |:2<br> | |||
(x + 2)² = 9 |<math>\surd</math><br> | |||
x<sub>1</sub> + 2 = - <math>\sqrt{9}</math> und x<sub>2</sub> + 2 = + <math>\sqrt{9}</math><br> | |||
x<sub>1</sub> + 2 = -3 und x<sub>2</sub> + 2 = 3 |-2<br> | |||
x<sub>1</sub> = - 3 - 2 und x<sub>2</sub> = + 3 - 2 <br> | |||
x<sub>1</sub> = -5 und x<sub>2</sub> = 1 <br> | |||
N<sub>1</sub>(-5|0) und N<sub>2</sub>(1|0)<br> | |||
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).<br> | |||
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann. | |||
<u><big>4. Form: Normalform f(x) = x² + px + q </big></u> | |||
Lösung mit der p-q-Formel:<br> | |||
Normalform: f(x) = x² + px + q<br> | |||
x² + px + q = 0<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{p}{2} \pm \sqrt{\left ( \frac{p}{2} \right )^2-q}</math><br> | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5<br> | |||
x<sub>1/2</sub> = -<math>\tfrac{-6}{2} \pm \sqrt{\left ( \frac{-6}{2} \right )^2-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math> \pm \sqrt{9-5}</math><br> | |||
x<sub>1/2</sub> = 3 <math>\pm \sqrt{4}</math><br> | |||
x<sub>1/2</sub> = 3<math> \pm </math>2<br> | |||
x<sub>1</sub> = 3 - 2 = 1 ; x<sub>2</sub> = 3+2 = 5 | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br> | |||
{{Lösung versteckt|1=<u><big>4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung ) | |||
Beispiel: f(x) = x² -6x + 5<br> | |||
f(x) = 0<br> | |||
x² - 6x + 5 = 0 | quadratische Ergänzung <math>\left ( \frac{6}{2} \right )^2 = 3^2</math><br> | |||
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel <br> | |||
(x - 3)² - 9 + 5 = 0 <br> | |||
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und geht wie in Bsp 3 vor: +4<br> | |||
(x - 3)² = 4 |<math>\surd</math><br> | |||
x<sub>1</sub> - 3 = -2 und x<sub>2</sub> - 3 = 2 |+3<br> | |||
x<sub>1</sub> = -2 + 3 und x<sub>2</sub> = 2 + 3 <br> | |||
x<sub>1</sub> = 1 und x<sub>2</sub> = 5 <br> | |||
N<sub>1</sub>(1|0) und N<sub>2</sub>(5|0)<br>|2=Lösung mit quadratischer Ergänzung|3=Verbergen}} | |||
====Quadratische Funktionen: Punktprobe==== | ====Quadratische Funktionen: Punktprobe==== | ||
Version vom 29. Dezember 2022, 17:57 Uhr
Funktionen
Lineare Funktionen
Diese Eigenschaften werden in folgendem Lied besungen.
Hier heißt die Funktionsgleichung f(x) = mx + n (n statt b, du findest in verschiedenen Büchern verschiedene Bezeichnungen).
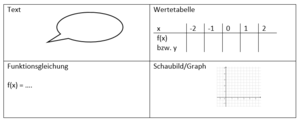
Lineare Funktionen: Wertetabelle
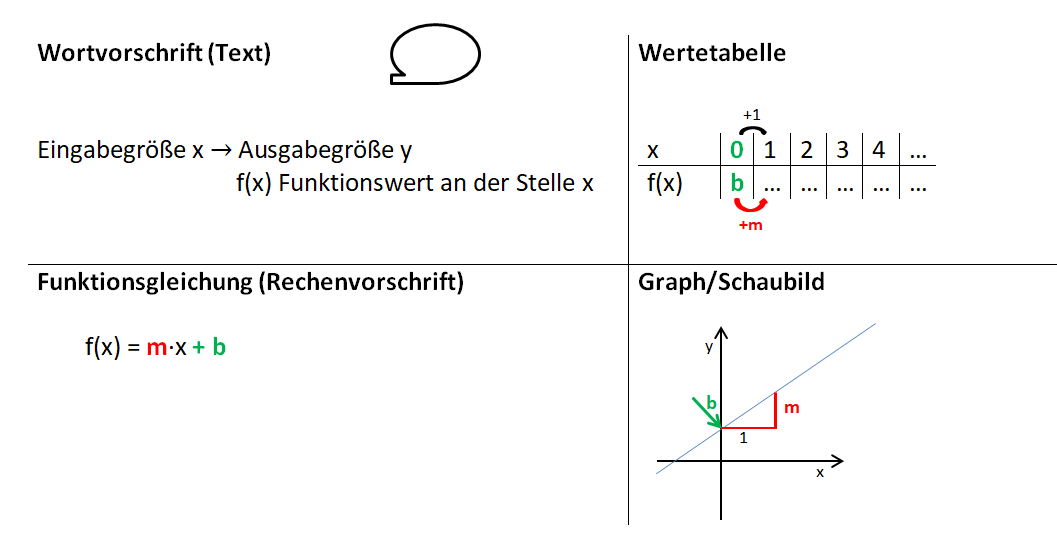
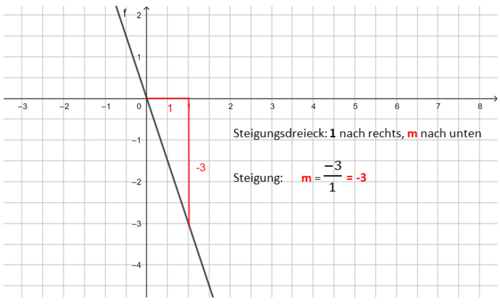
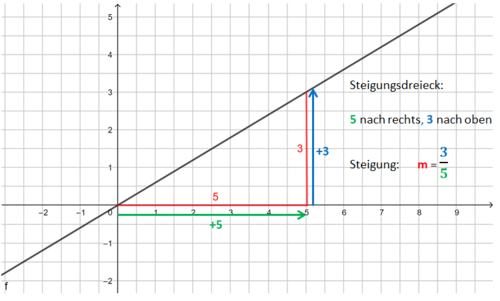
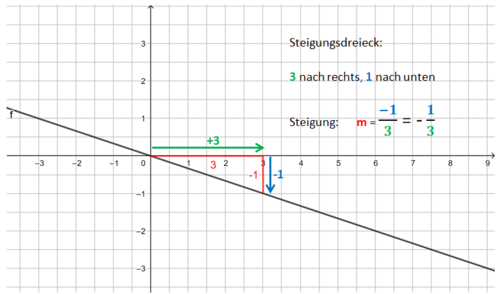
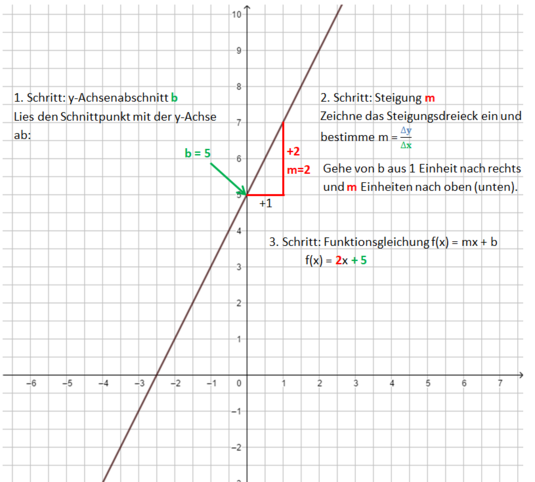
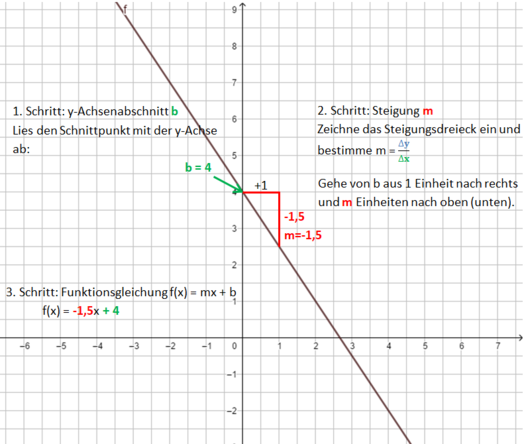
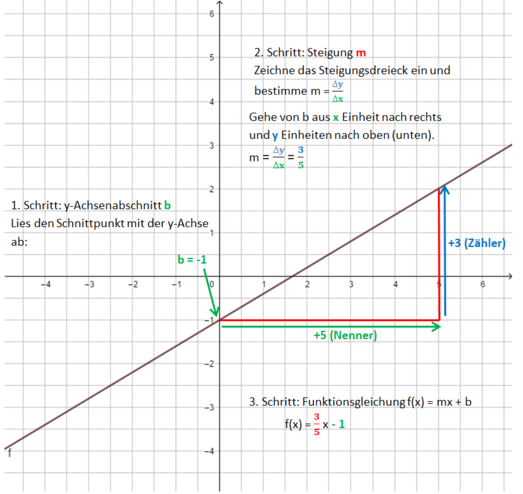
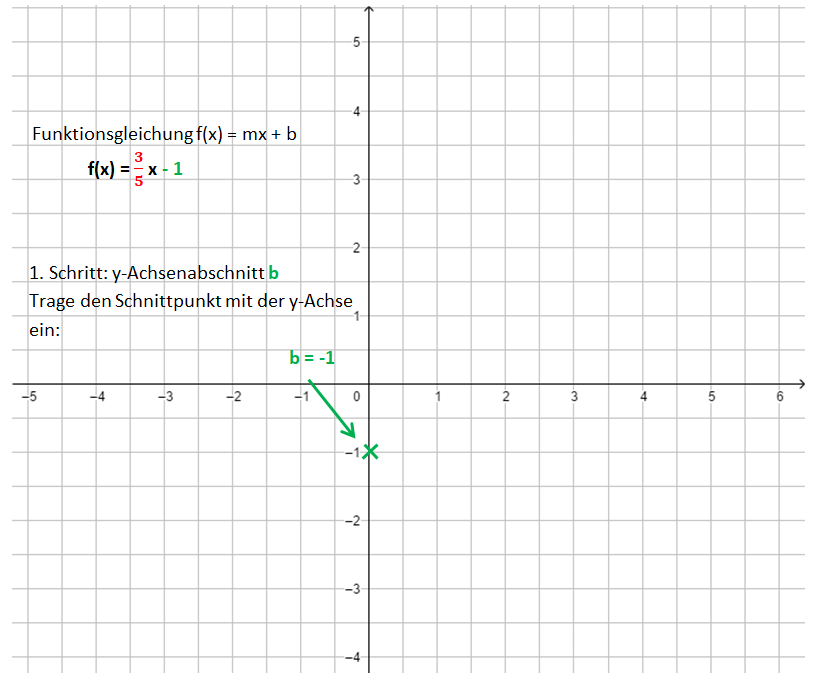
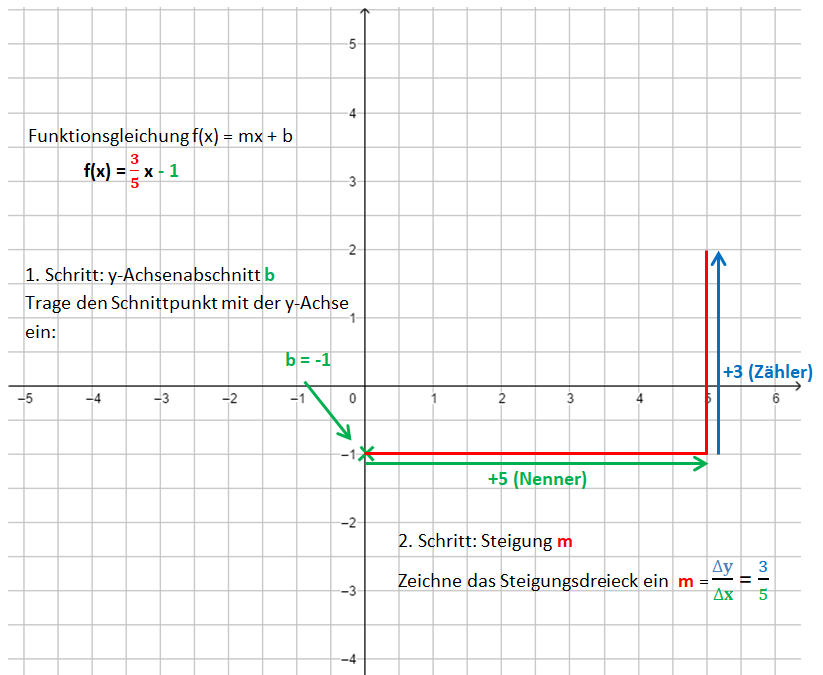
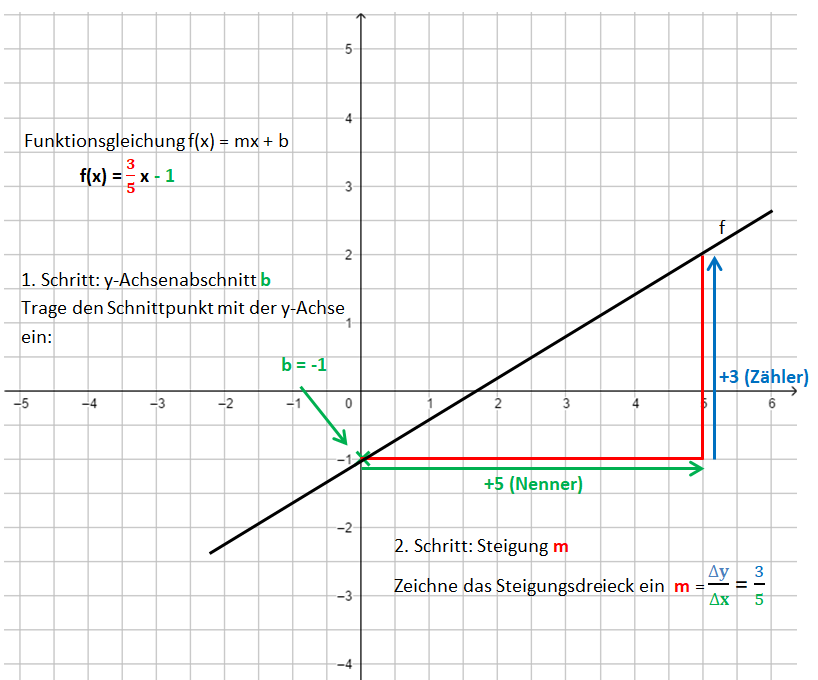
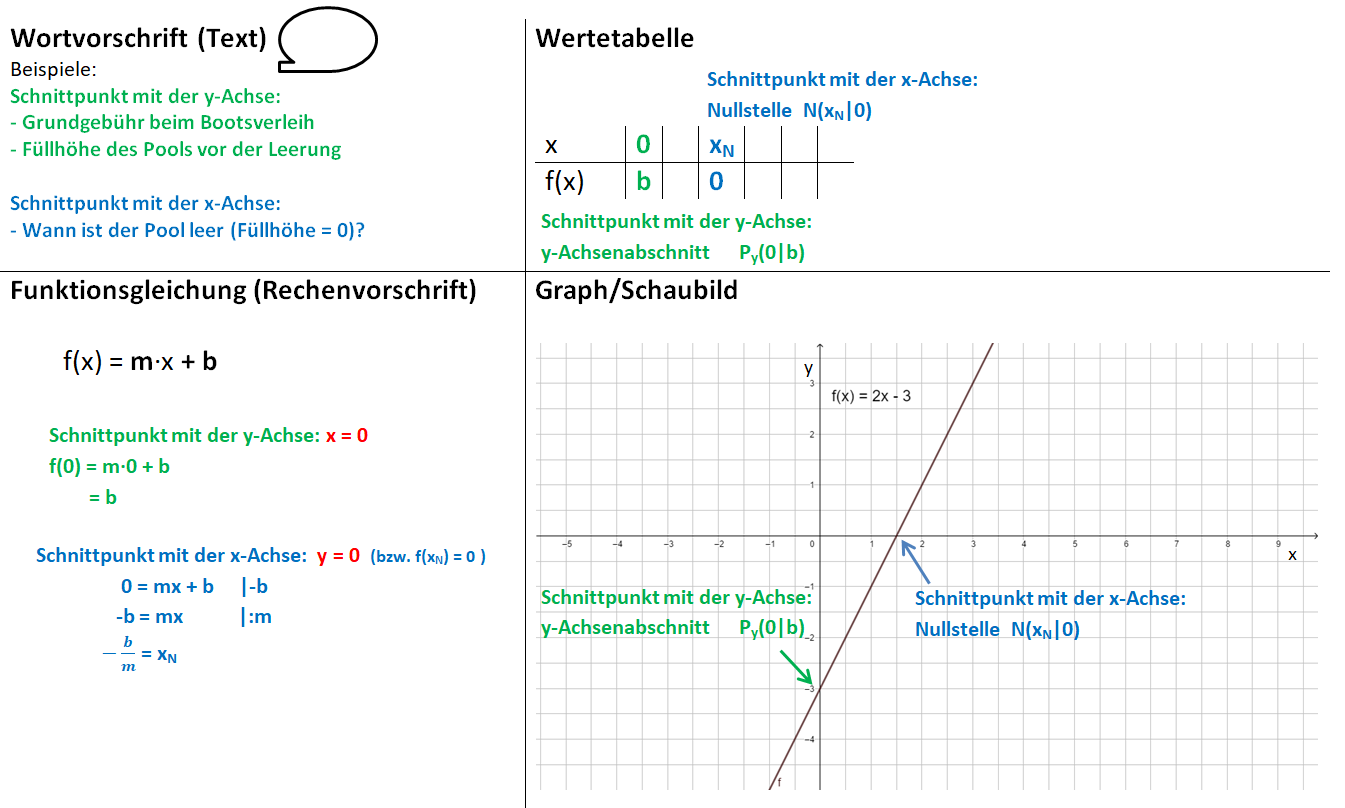
Lineare Funktionen: Gleichung und Graph
Beispiele:
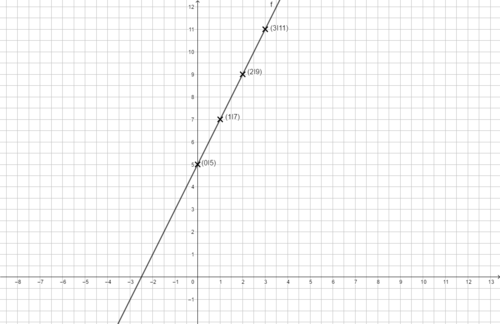
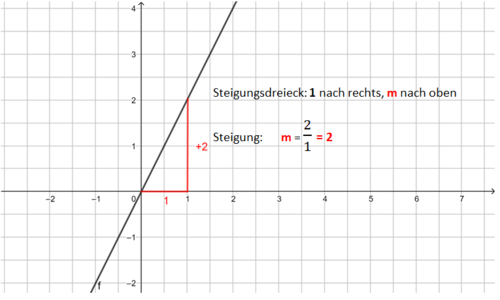
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Du kannst auch mithilfe von zwei Punkte die Gerade zeichnen bzw. die Funktionsgleichung bestimmen. Wie dur vorgehst, zeigt das Video.
Lineare Funktionen: Nullstellen bestimmen
Lineare Funktionen: Punktprobe
Quadratische Funktionen
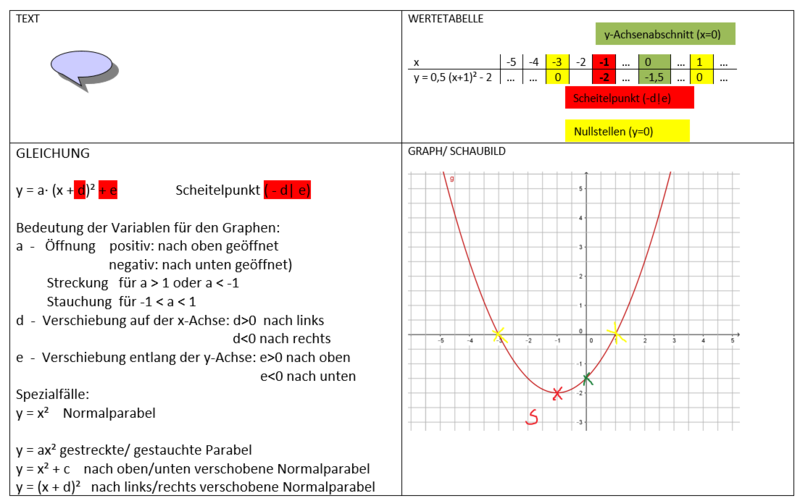
Die Scheitelpunktform quadratischer Funktionen
Quadratische Funktionen: Scheitelpunktform und Normalform
Du kannst die Formen der Quadratischen Funktionen umwandeln:
Beispiel:
f(x) = (x + 3)² - 4 |1. binomische Formel
= x² + 2·x·3 + 3² - 4
= x² + 6x + 9 - 4
= x² + 6x + 5
Die Normalform eignet sich gut zur Nullstellenberechnung, denn hier kannst du die p-q-Formel anwenden.
Beispiel:
f(x) = x² + 8x - 4 |quadratische Ergänzung = 4² = 16
= x² + 8x + 16 - 16 - 4 |1. binomische Formel
= (x + 4)² - 16 - 4
= (x + 4)² - 20
Also lautet der Scheitelpunkt S(-4|-20)
Quadratische Funktionen: Nullstellen bestimmen
Ist die Parabelgleichung in der Scheitelpunktform gegeben, kannst du die Anzahl der Nullstellen erkennen.
Je nach Lage des Scheitelpunktes und der Öffnung der Parabel hat diese keine, eine oder zwei Nullstellen:
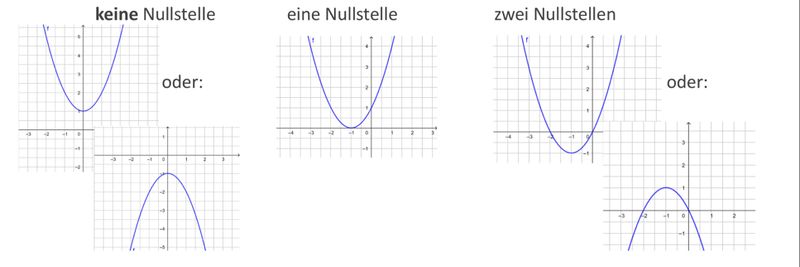
Tipp: Bestimme zunächst die Lage des Scheitelpunktes und die Öffnungsrichtung der Parabel. Ordne dann passend zu:
| keine | f(x) = x² + 3 | f(x) = -2x² - 5 | f(x) = (x+2)² + 1 |
| eine | f(x) = x² | f(x) = (x - 4)² | f(x) = -(x+2)² |
| zwei | f(x) = x² - 3 | f(x) = -2x² + 5 | f(x) = (x+2)² - 1 |
Beispiele:
1. Form: f(x) = ax²
Beispiel: f(x) = 3x²
f(x) = 0
3x² = 0 |:3
x² = 0 |
x = 0
N(0|0)
Natürlich hat jede Parabel mit der Funktionsgleichung f(x) = ax² die Nullstelle N(0|0), denn ihr Scheitelpunkt liegt im Ursprung. Der Scheitelpunkt ist also die Nullstelle.
2. Form: f(x) = ax² + c
Beispiel: f(x) = 0,5x² - 8
f(x) = 0
0,5x² - 8 = 0 |+8
0,5x² = 8 |:0,5
x² = 16 |
x1 = - und x2 = +
x1 = -4 und x2 = +4
N1(-4|0) und N2(4|0)
3. Form: Scheitelpunktform f(x) = a(x+d)²+e
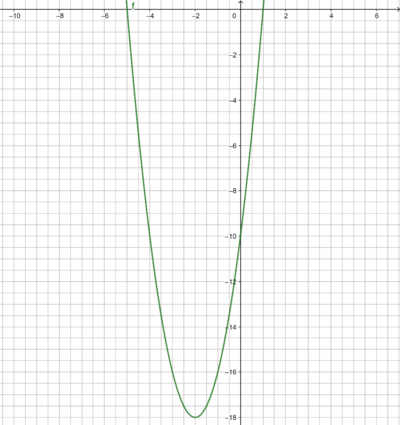
Beispiel: f(x) = 2(x + 2)² - 18
f(x) = 0
2(x + 2)² - 18 = 0 |+18
2(x + 2)² = 18 |:2
(x + 2)² = 9 |
x1 + 2 = - und x2 + 2 = +
x1 + 2 = -3 und x2 + 2 = 3 |-2
x1 = - 3 - 2 und x2 = + 3 - 2
x1 = -5 und x2 = 1
N1(-5|0) und N2(1|0)
Der Scheitelpunkt der Parabel liegt immer in der Mitte zwischen den beiden Nullstellen. Die x-Koordinate des Scheitelpunktes muss also -2 heißen. (x-Koordinate zwischen x = -5 und x = 1).
Dies passt zum Scheitelpunkt S(-2|-18), der aus der Parabelgleichung abgelesen werden kann.
4. Form: Normalform f(x) = x² + px + q
Lösung mit der p-q-Formel:
Normalform: f(x) = x² + px + q
x² + px + q = 0
x1/2 = -
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | pq-Formel mit p=-6 und q=5
x1/2 = -
x1/2 = 3
x1/2 = 3
x1/2 = 32
x1 = 3 - 2 = 1 ; x2 = 3+2 = 5
N1(1|0) und N2(5|0)
4. Form: Normalform f(x) = x² + px + q (mit quadratischer Ergänzung )
Beispiel: f(x) = x² -6x + 5
f(x) = 0
x² - 6x + 5 = 0 | quadratische Ergänzung
x² - 6x + 3² - 3² + 5 = 0 | 2. binomische Formel
(x - 3)² - 9 + 5 = 0
(x - 3)² - 4 = 0 | nun hast du wieder die Scheitelpunktform und geht wie in Bsp 3 vor: +4
(x - 3)² = 4 |
x1 - 3 = -2 und x2 - 3 = 2 |+3
x1 = -2 + 3 und x2 = 2 + 3
x1 = 1 und x2 = 5