Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 183: | Zeile 183: | ||
Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen. | Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen. | ||
[[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst durch | [[Datei:About icon (The Noun Project).svg|15px|middle]] Du kannst durch Klicken, Ziehen und Loslassen mit der Maus die Pyramide drehen. Außerdem kannst du auch die Zahlen genauso verschieben, um sie besser lesen zu können. | ||
<ggb_applet id="psnmcrma" width="1000" height="718" /> | <ggb_applet id="psnmcrma" width="1000" height="718" /> | ||
Version vom 22. November 2022, 18:35 Uhr
Wiederholung
Rechteckigen Flächeninhalt berechnen
Dreieckigen Flächeninhalt berechnen
Oberflächeninhalte berechnen
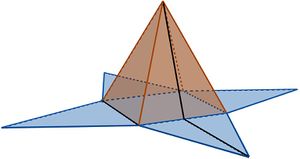
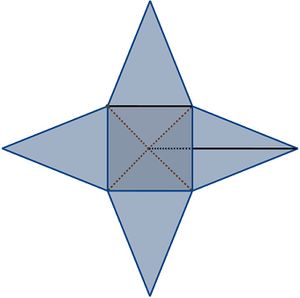
Wie du bereits im vorherigen Kapitel entdeckt hast, lässt sich die Oberfläche einer Pyramide in ein Netz überführen, indem man die Pyramide aufklappt und die Seitenflächen auf eine Ebene faltet.
Das so entstandene Netz besteht somit aus einer Grundfläche und den dreieckigen Seitenflächen, welche zusammen die sogenannte Mantelfläche bilden.
Den Flächeninhalt des gesamten Netzes nennt man den Oberflächeninhalt . Du kannst dir diese Größe als Menge an Verpackung vorstellen, die du benötigst, um das pyramidenförmige Objekt zu umschließen.
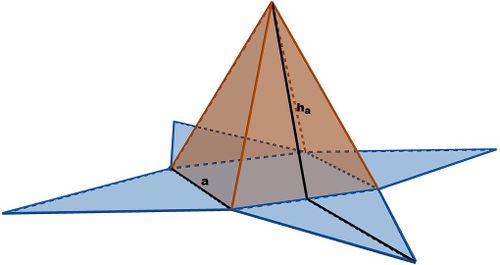
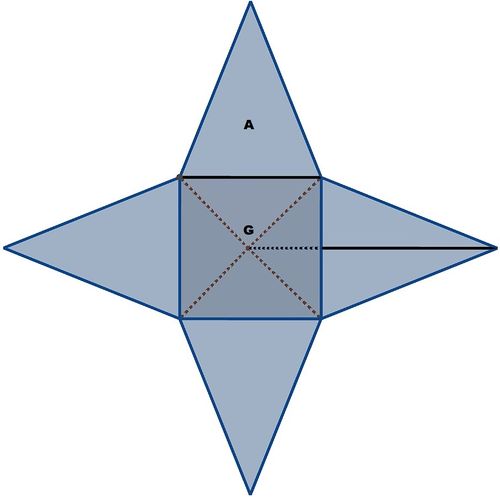
Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken.
Pyramiden schätzen
Vertiefen und Vernetzen