Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 48: | Zeile 48: | ||
{{Box | Aufgabe 4: Dreieckige Flächeninhalte berechnen | | {{Box | Aufgabe 4: Dreieckige Flächeninhalte berechnen | | ||
'''a)''' <math>g=16\text{ m}, h=7\text{ m}</math> | '''a)''' <math>g=16\text{ m}, h=7\text{ m}</math> | ||
| Zeile 136: | Zeile 135: | ||
{{Box | Beispiel: Oberflächeninhalt berechnen | | {{Box | Beispiel: Oberflächeninhalt berechnen | | ||
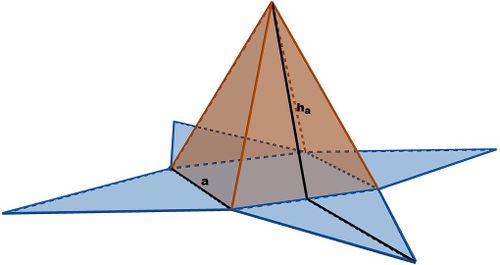
Betrachte die Pyramide rechts, mit einer Kantenlänge von <math>a = 5\text{ cm}</math> und einer Seitenhöhe von <math>h_a = 6\text{ cm}</math>. | Betrachte die Pyramide rechts, mit einer Kantenlänge von <math>a = 5\text{ cm}</math> und einer Seitenhöhe von <math>h_a = 6\text{ cm}</math>. | ||
| Zeile 303: | Zeile 301: | ||
{{Box| | {{Box|Aufgabe 12: Zusammengesetzte Körper| | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Kehre zum Arbeitsblatt zurück und bearbeite dort die Aufgabe 12.''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Kehre zum Arbeitsblatt zurück und bearbeite dort die Aufgabe 12.''' | ||
| Zeile 333: | Zeile 331: | ||
{{Box| | {{Box|Aufgabe 13: Tipi| | ||
[[Datei:Teepee and Clifford King (14059271679).jpg|mini|alternativtext=|Tipi]] | [[Datei:Teepee and Clifford King (14059271679).jpg|mini|alternativtext=|Tipi]] | ||
Version vom 21. November 2022, 17:49 Uhr
Wiederholung
Rechteckigen Flächeninhalt berechnen
Dreieckigen Flächeninhalt berechnen
Oberflächeninhalte berechnen
Lies dir eine der folgenden Situationsbeschreibungen durch und bearbeite anschließend Aufgabe 6.
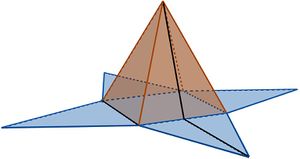
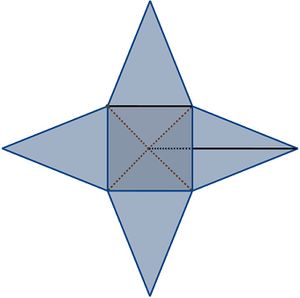
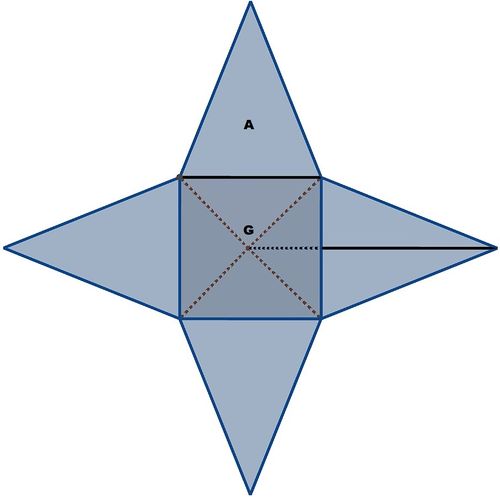
Wie du bereits im vorherigen Kapitel entdeckt hast, lässt sich die Oberfläche einer Pyramide in ein Netz überführen, indem man die Pyramide aufklappt und die Seitenflächen auf eine Ebene faltet.
Das so entstandene Netz besteht somit aus einer Grundfläche und den dreieckigen Seitenflächen, welche zusammen die sogenannte Mantelfläche bilden.
Den Flächeninhalt des gesamten Netzes nennt man den Oberflächeninhalt . Du kannst dir diese Größe als Menge an Verpackung vorstellen, die du benötigst, um das pyramidenförmige Objekt zu umschließen.
Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken.
Pyramiden schätzen
Vertiefen und Vernetzen