Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden vermessen

zurück zur Kapitelauswahl

Info

In diesem Lernpfadkapitel lernst du

• wie du von Pyramiden den Oberflächeninhalt schätzen kannst.
• wie du von Pyramiden den Oberflächeninhalt berechnen kannst.

Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Wiederholung

Info

Um die Oberfläche einer Pyramide zu bestimmen, ist es wichtig, dass du weißt, wie man den Flächeninhalt von Rechtecken und von Dreiecken bestimmt. Wenn du dich noch daran erinnerst, wie man diesen bestimmt, kannst du direkt zu Aufgabe 5 gehen. Wenn du dir noch etwas unsicher bist und eine kurze Wiederholung brauchst, bearbeite die folgenden Aufgaben (Aufgaben 1,2,3 und 4).

Rechteckigen Flächeninhalt berechnen

Aufgabe 1: Flächeninhalt vom Rechteck

Berechne den Flächeninhalt des folgenden Quadrates (denke auch daran, die richtige Einheit anzugeben):

Zur Berechnung des Flächeninhaltes benötigst du nicht die Diagonale.

Die Formel zur Berechnung eines rechteckigen Flächeninhaltes lautet: $A=a \cdot b$

$A=4 \text{ cm} \cdot 3 \text{ cm} =12 \text{ cm²}$

Dreieckigen Flächeninhalt berechnen

Aufgabe 2: Flächeninhalt vom Dreieck

Berechne den Flächeninhalt des folgenden Dreiecks (denke auch daran, die richtige Einheit anzugeben):

Du benötigst zur Berechnung eines dreieckigen Flächeninhaltes die Höhe und die Grundseite.

Die Formel zur Berechnung eines dreieckigen Flächeninhaltes lautet: $A=\tfrac{g \cdot h}{2}$

$A= \tfrac{4 \text{ cm} \cdot 6 \text{ cm}}{2} =12 \text{ cm²}$

Info

In den Aufgaben 3 und 4 hast du noch einmal die Möglichkeit, das Bestimmen von recht- und dreieckigen Flächeninhalten zu üben. Solltest du dich schon sicher fühlen, kannst du auch direkt mit Aufgabe 5 weitermachen.

Aufgabe 3: Rechteckige Flächeninhalte berechnen

a) $a=7\text{ m}, b=5\text{ m}$

$A=35\text{ m}^{2}$

b) $a=90\text{ dm}, b=2\text{ m}$

$A=18\text{ m}^{2}, A=1800\text{ dm}^{2}$

Aufgabe 4: Dreieckige Flächeninhalte berechnen

a) $g=8\text{ m}, h=3\text{ m}$

$A=12\text{ m}^{2}$

b) $g=3\text{ m}, h=800\text{ cm}$

$A=12\text{ m}^{2}, A=1200\text{ dm}^{2}, A=120000\text{ cm}^{2}$

Aufgabe 5: Formeln notieren

Kehre nun zum Arbeitsblatt zurück und trage die Formeln zur Berechnung rechteckiger und dreieckiger Flächeninhalte ein (die vollständigen Formeln stehen jeweils unter "Tipp 2" in Aufgabe 1 und Aufgabe 2).

Oberflächeninhalte berechnen

Lies dir eine der folgenden Kurzgeschichten durch und löse anschließend den nachstehenden Arbeitsauftrag.

1981 initiierte der damalige französische Staatspräsident das Projekt „Grand-Louvre“. Im Rahmen dessen wurde der Architekt Ieoh Ming Pei beauftragt, die heutige Glaspyramide im Zentrum des Palastes zu entwickeln. Die Blaupause steht und die Vision ist klar: Die Pyramide soll komplett mit Glas umfasst werden! Nun geht es darum zu ermitteln, wie viele der rautenförmigen Glasscheiben hergestellt werden müssen.

Die Cheops-Pyramide ist die älteste und größte der drei Pyramiden von Gizeh und wird deshalb auch als „Große Pyramide“ bezeichnet. Diese höchste Pyramide der Welt wurde als Grabmal für den Pharao Cheops etwa 2620 v. Chr. errichtet und gilt heutzutage als eines der sieben Weltwunder der Antike. Natürlich mussten ausreichend Steine gehauen werden, um den Bau zu vollenden. Der zuständige Untertan stand vor der Aufgabe, die passende Anzahl zu berechnen.

Im Zweiten Weltkrieg wurde der St.-Paulus-Dom in Münster durch Bombentreffer schwer beschädigt. In den Jahren 1946 bis 1956 wurde der Dom wieder aufgebaut. Unter anderem mussten die pyramidenförmigen Kirchturmspitzen wieder mit neuen Dachziegeln belegt werden, doch die Materialien in der Nachkriegszeit waren knapp. Somit soll eine möglichst passende Anzahl berechnet werden.

 

Aufgabe 6: Materialien berechnen

Überlege dir bei einer der Geschichten, wie man das Problem mathematisch lösen könnte. Schreibe deine Überlegungen auf und stell dir dabei vor, du müsstest deinen Arbeitgeber von deinen Überlegungen überzeugen.

Kannst du dein Vorgehen auch verallgemeinern und auf die anderen Probleme anwenden? Falls dir dies schwerfällt, schau dir genau den nächsten Abschnitt an!

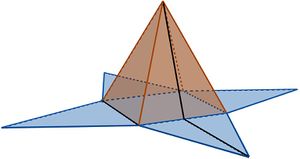
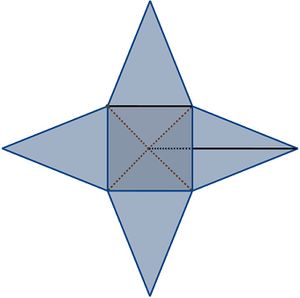
Wie du bereits im vorherigen Kapitel entdeckt hast, lässt sich die Oberfläche einer Pyramide in ein Gitternetz überführen, indem man die Pyramide 'aufklappt' und die Seitenflächen auf eine Ebene projiziert.

Das so entstandene Gitternetz besteht somit aus einer Grundfläche $G$ und den dreieckigen Seitenflächen, welche zusammen die sogenannte Mantelfläche $M$ bilden.

Den Flächeninhalt des gesamten Gitternetzes nennt man den Oberflächeninhalt $O$. Du kannst dir diese Größe als Menge an Verpackung vorstellen, die du benötigst, um das pyramidenförmige Objekt zu umschließen.

Merksatz: Oberflächeninhalt

Der Oberflächeninhalt einer Pyramide lässt sich durch die Summe ihrer Grundfläche und ihrer Mantelfläche berechnen. Als Formel ergibt sich somit:

$O = M + G$.

Die Mantelfläche besteht aus mehreren dreieckigen Seitenflächen. Die Anzahl dieser Seitenflächen ist gleich der Anzahl der Ecken der Grundfläche.

Im Falle einer quadratischen Pyramide, welche ihre Spitze über der Mitte ihrer Grundfläche hat, ergibt sich für die Grundfläche die Fläche eines Quadrates und für ihre Mantelfläche die Flächeninhalte von vier gleich großen Dreiecken.

Beispiel: Oberflächeninhalt berechnen

Sei wie oben rechts eine Pyramide gegeben, mit einer Kantenlänge von $a = 5\text{ cm}$ und einer Seitenhöhe von $h_a = 6\text{ cm}$.

Grundfläche G:

$G = a \cdot a$

$G = 5 \cdot 5 = 25$

$G = 25 \text{ cm²}$.

Seitenfläche A:

$A = \frac{1}{2} \cdot a\cdot h_a$

$A = \frac{1}{2} \cdot 5 \cdot 6 = 15$

$A = 15\text{ cm²}$

Mantelfläche M:

$M = 4 \cdot A$

$M = 4 \cdot 15 = 60$

$M = 60\text{ cm²}$.

Oberfläche O:

$O = G + M$

$O = 25 + 60 = 85$

$O = 85\text{ cm²}$

Idee

Um Aufgabe 6 zu lösen, wäre somit ein geeigneter Ansatz, die Mantelfläche der pyramidenförmigen Gebilde zu berechnen. Anstatt die Materialien einzeln zu zählen, bedarf es demnach nur der Kantenlänge und der Seitenhöhe.

Aufgabe 7: Lückentext 'Rechteckige Pyramide'

Aufgabe 8: Oberflächeninhalte verschiedener Pyramiden berechnen

Kehre nun zum Arbeitsblatt zurück und bearbeite die Aufgabe 8 zum Einüben des Verfahrens.

Aufgabe 9: Tetraeder?

Azra hat zur Berechnung an einer Pyramide mit dreieckiger Grundfläche sehr viele Größen gemessen, um auf alles vorbereitet zu sein. Allerdings sollte sie nur den Oberflächeninhalt berechnen.

Kevin erwidert, dass dies ja viel zu viel Arbeit sei, da man doch nur eine der Seitenflächen benötigt. Schnell berechnet er:

$O = G + 3 \cdot A = \frac{1}{2} \cdot 6.4 \cdot 3.12 + \frac{1}{2} \cdot 15.4 \cdot 6 = 56,109$.

Stimmst du diesem Ergebnis zu oder war Kevin doch etwas zu voreilig? Berechne dazu selbst den Oberflächeninhalt und vergleiche dein Ergebnis!

Tatsächlich unterscheiden sich bei dieser Pyramide die Kantenlängen, da es sich nicht um ein gleichseitiges Dreieck als Grundfläche handelt. Somit sind auch die Seitenflächen nicht deckungsgleich und müssen einzeln berechnet werden.

$O = G + M$

$O = G + A_a + A_b + A_c$

$O = G + \frac{1}{2} \cdot a \cdot h_a + \frac{1}{2} \cdot b \cdot h_b + \frac{1}{2} \cdot c \cdot h_c$

Der Oberflächeninhalt lautet $O = 57,563$

Pyramiden schätzen

Im Alltag kommt es manchmal vor, dass man nicht alle Angaben kennt, die man zur Bestimmung der Oberfläche benötigt. In diesem Abschnitt kannst du deshalb üben, einzelne Angaben oder auch den gesamten Flächeninhalt zu schätzen. Dabei kommt es nicht so sehr darauf an, dass du immer komplett richtig schätzt (das wäre ja auch so gut wie unmöglich), sondern, dass du ein Gefühl für die Größen entwickelst.

Aufgabe 10: Oberfläche von Pyramiden schätzen

Ordne jedem Bild durch Schätzen den passenden Oberflächeninhalt zu (du musst hier nichts rechnen!):

Sortiere die Größen erstmal grob bevor du sie den Bildern zuordnest.

Aufgabe 11: Oberfläche berechnen mit unbekanntem Parameter

Auf dem Bild rechts siehst du das Luxor Hotel und Casino. Es steht in Las Vegas und zeichnet sich vor allem durch seine Pyramidenform aus. Die Außenfassade besteht fast vollständig aus Glas und muss natürlich regelmäßig geputzt werden. Dafür soll eine neue Reinigungsfirma engagiert werden. Diese möchte aber vorab wissen, wie viele Quadratmeter circa zu putzen sind. Du weißt, dass das Gebäude $107 \text{ m}$ hoch ist und $106,7 \text{ m}$ breit.

a) Welche Angabe, die du zur genauen Berechnung der zu reinigenden Fläche benötigst, fehlt?

Achte genau darauf, welche Höhe gegeben ist und welche Höhe du zur Berechnung der Seitenflächen benötigst.

Es fehlt die Höhe $h_a$ der dreieckigen Seitenflächen.

b) Berechne die Größe der zu reinigenden Fläche, indem du die fehlende Angabe schätzt.

Das Luxor Hotel und Casino spielte auch schon in Aufgabe 10 eine Rolle. Vergleiche dein Ergebnis mit der Lösung aus Aufgabe 10, um zu sehen, ob du gut geschätzt hast.

Aufgabe 12

Kehre nun zum Arbeitsblatt zurück und bearbeite die Aufgabe 12.

Aufgabe 13: Oberfläche vom Louvre schätzen

Unter folgendem Link [[1]] findest du eine Streetview-Ansicht vom Louvre. Bestimme nun den Oberflächeninhalt der Glasfläche, indem du die benötigten Parameter vorerst schätzt.

Denke zurück an dein Vorgehen aus Aufgabe 6.

Nutze Personen als Referenzgröße.

Ob du gut geschätzt hast, siehst du im Kapitel 4 "Pyramiden verknüpfen".

Vertiefen und Vernetzen

In diesem Abschnitt findest du vertiefende Aufgaben zu dem Oberflächeninhalt von Pyramiden und darüber hinausgehenden Themen. Neben Pyramiden kommen in diesem Abschnitt auch weitere Körper bzw. Flächen vor, die du zum Teil bereits aus dem Unterricht kennst. Die Aufgaben sind als Knobelaufgaben gedacht, sodass du hier testen kannst, wie fit du im Umgang mit den Oberflächeninhalten von Pyramiden und ähnlichen Körpern bist.

Aufgabe 14: Zusammengesetzte Körper

Die 23 Schülerinnen und Schüler einer fünften Klasse sollen vor Weihnachten in der Schule eigene Nikolaushäuschen bauen, die einen quaderförmigen Körper mit einem Walmdach haben sollen. Ein Modell dieses Häuschens siehst du in dem GeoGebra-Applet abgebildet.

Folgende Daten soll das Häuschen haben: $a=6 \text{ cm}, b=1,2 \text{ dm}, c=0,5 \text{ dm}, d=6 \text{ cm}, h_a=5 \text{ cm}, h_b=5 \text{ cm}$.

Berechne, wie viel Pappe die Lehrkraft mitbringen muss, wenn alle Schülerinnen und Schüler der Klasse ein Häuschen bauen sollen.

Die Dachfläche besteht aus zwei gleich großen Trapezen und zwei gleich großen Dreiecken.

Die Formel für den Flächeninhalt dieser Trapeze lautet: $A=\frac{b+d}{2} \cdot h_b$

Wir berechnen als erstes den Oberflächeninhalt des Quaders. Die Grundfläche berechnet sich aus

$G=a \cdot b=6 \cdot 12=72 \text{ cm²}$.

Als nächstes wird die Mantelfläche des Quaders berechnet.

$M_{Quader}=2 \cdot a \cdot c+2 \cdot b \cdot c=2 \cdot 6 \cdot 5+2 \cdot 12 \cdot 5=60+120=180 \text{ cm²}$

Nun berechnen wir die Mantelfläche des Walmdaches. Zunächst berechnen wir die Fläche des Dreiecks:

$A_{Dreick}=\frac{1}{2} \cdot a \cdot h_a=\frac{1}{2} \cdot 6 \cdot 5=15 \text{ cm²}$.

Nun fehlt noch die Fläche des Trapezes:

$A_{Trapez}=\frac{b+d}{2} \cdot h_b=\frac{12+6}{2} \cdot 5=45 \text{ cm²}$.

Wir erhalten insgesamt für die Mantelfläche des Walmdaches:

$M_{Walmdach}=2 \cdot A_{Dreick}+2 \cdot A_{Trapez}=2 \cdot 15+2 \cdot 45=30+90=120 \text{ cm²}$.

Insgesamt erhalten wir also: $O=G+M_{Quader}+M_{Walmdach}=72+180+120=372 \text{ cm²}$.

Für 23 Schülerinnen und Schüler muss die Lehrkraft also $23 \cdot 372=8556 \text{ cm²}$ Papier mitbringen.

Aufgabe 15: Pyramidenstumpf

Slovak Radio Building

Das Slovak Radio Building in Bratislava (Slowakei) hat die Form eines umgedrehten quadratischen Pyramidenstumpfes. Das Gebäude soll eine neue Glasfassade sowie ein neues Glasdach erhalten, die aus Sicherheitsglas bestehen sollen. Das Gebäude ist an der unteren Kante $22,59 \text{ m}$ breit, an der oberen Kante $74,33 \text{ m}$ breit und ist $42,7 \text{ m}$ hoch. Die Seitenhöhe der Fassade beträgt $49,7 \text{ m}$.

a) Berechne, wie viel Quadratmeter des Sicherheitsglases für die neue Fassade und das Dach benötigt werden. Runde auf zwei Stellen nach dem Komma.

Die Seitenflächen des Gebäudes sind trapezförmig.

Die Formel für die Berechnung des Flächeninhaltes eines Trapezes lautet: $A=\frac{a+c}{2} \cdot h$

Wir berechnen die Lösung nach der oben aufgestellten Formel: $O=M+G.$

Die Mantelfläche besteht hier aus vier identischen Trapezen, mit den Kantenlängen $a=74,33\text{ m}, c=22,59\text{ m}$ und der Höhe $h_a=49,7\text{ m}$. Es gilt somit für eine Seitenfläche:

$A_{Trapez}=\frac{a+c}{2} \cdot h_a=\frac{74,33+22,59}{2} \cdot 49,7=2408,462 \text{ m²} \approx 2408,46 \text{ m²}$.

Für die Mantelfläche folgt dann: $M=4 \cdot A_{Trapez}=4 \cdot 2408,46=9633,84 \text{ m²}$.

Die Grundfläche ist in diesem Fall das Dach des Gebäudes, welches ebenfalls aus Glas bestehen soll:

$G=a^2=74,33 \cdot 74,33=5524,9489 \text{ m²} \approx 5524,95 \text{ m²}$

Zusammen gilt dann: $O=M+G=9633,84+5524,95=15158,79 \text{ m²}$

Es werden insgesamt $15158,79 \text{ m²}$ Sicherheitsglas benötigt.

b) Das Sicherheitsglas kostet im Handel ungefähr $75 \text{ €/m²}$. Bei der Montage der Fassade werden immer einige Glasplatten beschädigt, sodass 2% mehr Glas gekauft wird, als eigentlich für die Fassade benötigt wird. Berechne, wie hoch die Materialkosten sind, die für die neue Fassade entstehen.

Wir berechnen zunächst die zu bestellende Glasmenge: $15158,79 \cdot 1,02=15461,9658 \text{ m²} \approx 15461,97 \text{ m²}$

Nun folgt für den Materialpreis: $15461,97 \cdot 75=1159647,75 \text{ €}$

Das Material für die neue Fassade kostet insgesamt $1159647,75 \text{ €}$

Aufgabe 16: Tipi

Tipi

Für ein Tipi-Modell soll eine Plane hergestellt werden. Das Tipi ist in der Abbildung rechts maßstabsgetreu abgebildet. Zur Vereinfachung kannst du annehmen, dass das Tipi die Form einer regelmäßigen achteckigen Pyramide hat, die an einer der Seitenflächen eine halbrunden Öffnung enthält. Der Boden des Tipis wird nicht mit einer Plane ausgekleidet.

Berechne, wie viel Quadratmeter Zeltplane für ein Tipi benötigt wird.

Schätze die benötigten Größen zur Berechnung der Fläche, indem du den abgebildeten Menschen als Referenzgröße verwendest.

Der gesuchte Flächeninhalt berechnet sich aus der Mantelfläche abzüglich des halbrunden Eingangs.

Bei dem Eingang handelt es sich um einen Halbkreis. Der Flächeninhalt dieses Halbkreises lässt sich mit der Formel $A=\frac{1}{2} \cdot \pi \cdot r^2$ berechnen.

Wir berechnen zunächst die Mantelfläche der achteckigen Pyramide. Dazu müssen wir zunächst die fehlenden Daten schätzen. Wir nehmen an, dass der Mensch ungefähr $1,70 \text{ m}$ groß ist. Wir schätzen daher, dass die Seitenhöhe des Tipis ungefähr $4,1 \text{ m}$ beträgt (da wir die Gesamthöhe auf ungefähr $3,8 \text{ m}$ geschätzt haben). Die Breite einer Grundkante schätzen wir auf ungefähr $1,3 \text{ m}$ (da wir den Durchmesser des Achtecks auf $3,5 \text{ m}$ geschätzt haben). Wir berechnen zunächst den Flächeninhalt einer einzelnen Seitenfläche (also eines Dreiecks) der achteckigen Pyramide:

$A_{Dreieck}=\frac{1}{2} \cdot 1,3 \cdot 4,1=2,665 \text{ m²} \approx 2,67 \text{ m²}$

Als nächstes berechnen wir den Mantelflächeninhalt der Pyramide: $M=8 \cdot A_{Dreieck}=8 \cdot 2,67=21,36 \text{ m²}$

Wir schätzen den Durchmesser des Halbkreises auf $1,5 \text{ m}$. Nun berechnen wir den Flächeninhalt des Halbkreises und ziehen diesen dann von der Mantelfläche ab:

$A_{Kreis}=\frac{1}{2} \cdot 0,75^2 \cdot \pi \approx 0,88 \text{ m²} \Rightarrow A_{gesucht}=21,36-0,88=20,48 \text{ m²}$

Für ein Tipi werden ungefähr $20,48 \text{ m²}$ Zeltplane benötigt.

weiter zum nächsten Kapitel