Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden verknüpfen

Dieser Lernpfad befindet sich aktuell im Aufbau.

Info

Herzlich Willkommen in dem Kapitel „Pyramiden verknüpfen“!

Hier kannst du dein bereits erworbenes Wissen zum Thema Pyramiden vertiefen.

Checkliste - Das brauchst du

Checkliste

Für dieses Kapitel solltest du...

• die Oberfläche einer Pyramide berechnen können.

• den Satz des Pythagoras anwenden können.

Falls du den Satz des Pythagoras noch einmal wiederholen möchtest, kannst du dein Wissen in Aufgabe 1 auffrischen. Wenn du dich schon sicher im Umgang mit dem Satz des Pythagoras fühlst, kannst du direkt mit Aufgabe 2 fortfahren.

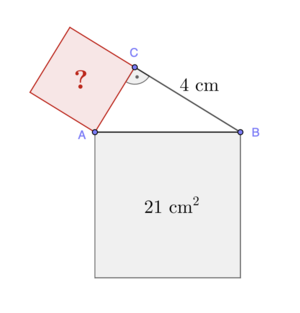
Satz des Pythagoras

Aufgabe 1: Wiederholung des Satzes von Pythagoras

a) Ergänze den Lückentext mit den bereits bekannten Begriffen des Satzes von Pythagoras.

Klicke zum Ausfüllen auf die Lücken und wähle aus den angegebenen Vorschlägen aus. Kontrolliere deine Lösung mit dem blauen Haken.

b) Berechne den Flächeninhalt des roten Quadrats. Nutze für die Berechnung das Arbeitsblatt „Pyramiden verknüpfen“.

Schau dir das Applet an. Kannst du das Applet auf die Aufgabe beziehen?

Du kannst die Eckpunkte A, B und C des Dreiecks verschieben und dir so den Satz des Pythagoras veranschaulichen.

Merke: Für den Flächeninhalt A eines Quadrats mit der Seitenlänge a gilt: $A = a^2$.

$(4 cm)^2 + b^2 = 21cm^2$

$\Leftrightarrow b^2 = 21 cm^2 - (4 cm)^2$

$\Leftrightarrow b^2 = 21 cm^2 - 16 cm^2$

$\Leftrightarrow b^2 = 5 cm^2$

Aufgabe 2: Sightseeing in Paris 1 - Der Louvre

Für diese Aufgabe benötigst du das Arbeitsblatt „Pyramiden verknüpfen“ (Lernpfadaufgaben, S. ???).

Glaspyramide im Innenhof des Louvre.

Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum Louvre teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche.

Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: „Wie lang sind die Edelstahlträger an den Seitenkanten der Pyramide?" Der Touristenführer weiß nur, dass die Pyramide 21 Meter hoch ist.

a) Untersuche, ob diese Angabe genügt, um die Länge eines Stahlträgers zu berechnen. Falls dem nicht so ist, gib Größen an, die zusätzlich benötigt werden.

b) Ein anderer Tourist findet im Internet eine Angabe zur Seitenlänge der quadratischen Grundfläche von 35 Metern. Berechne mithilfe der gegeben Größen die Länge eines Stahlträgers an der Seitenkante der Pyramide.

Zeichne zur Veranschaulichung eine passende Pyramide in dein Heft. Du kannst zur Berechnung der gesuchten Seite den Satz des Pythagoras beliebig oft anwenden.

Überlege dir Hilfsdreiecke innerhalb der Pyramide, in denen du den Satz des Pythagoras anwenden kannst.

Im nachstehenden GeoGebra-Applet kannst du dir durch das Anklicken der einzelnen Boxen mögliche Hilfsdreiecke anzeigen lassen.MANCHMAL WIRD DIE GRÖ?E DES APPLETS ZUFÄLLIG VIEL ZU GROß ODER KLEIN ANGEZEIGT:NACH NEULADEN PASSTS WIEDER

Die Länge eines Stahlträgers der Pyramide beträgt etwa $32,46~\mathrm{m}^2$.

c) Ebenfalls kam die Frage auf, wie viele Quadratmeter Glasfläche die Reinigungsfirma von außen putzen muss. Beantworte die Frage durch mathematische Rechnungen.

Die Größe der Glasfläche entspricht der Mantelfläche der Pyramide.

Du kannst die berechnete Länge eines Stahlträgers aus b) verwenden und damit in einem geeigneten Hilfsdreieck die Seitenhöhe der Pyramide bestimmen.

Eine Glaswand besitzt eine Fläche von etwa $27,34~\mathrm{m}^2$. Die gesamte Glasfläche der Pyramide beträgt demnach rund $109,34~\mathrm{m}^2$.

d) Erkennst du in deiner Rechnung aus b) und c) verschiedene Teilschritte? Markiere und benenne sie in deinen Aufzeichnungen.

Checkliste zur Bestimmung der Mantelfläche

In Aufgabe 4 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet. In dem folgenden Applet wird die allgemeine Vorgehensweise noch einmal zusammengefasst. Bringe die einzelnen Teilschritte in die richtige Reihenfolge und übertrage die Checkliste anschließend auf dein Arbeitsblatt.

Aufgabe 3: Der Eiffelturm

Als nächster Stopp steht der Eiffelturm auf eurer Liste.

Da momentan das Gerüst des Eiffelturms erneuert wird, dienen 4 Stützen in den Torbögen als Stabilisierung. Du möchtest gerne wissen wie lang diese Stützen sind. Dazu entnimmst du einer Informationstafel am Eiffelturm einige wichtige Maße des Bauwerks und versuchst die Berechnung näherungsweise anhand einer Pyramide mit quadratischer Grundfläche durchzuführen.

Du fertigst anhand der Daten eine Skizze an und schätzt die Höhe der Pyramide (grün) auf 140m. Die Stützen markierst du in deiner Zeichnung rot.

Du benötigst eine zweite Hilfspyramide zur Berechnung. Diese ist in der Abbildung orange gekennzeichnet.

Die Stützen haben eine Länge von 44,85 Metern.

Aufgabe 4: Der Würfel

Aus mehreren gleichartigen Pyramiden lässt sich der unten abgebildete Würfel formen. Überlege dir, wie du die Pyramiden zusammensetzen kannst, wie viele du benötigst, um den Würfel auszufüllen und wie diese Pyramiden aussehen.

a) Was für eine Grundfläche hat die Pyramide? Welche Seitenlängen hat die Grundfläche deiner Pyramide?

b) Welche Höhe hat die Pyramide?

Schau dir das Applet an und bediene den Schieberegler an der linken Seite. Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht?

c) Berechne die Länge der orange markierten Strecke. Runde dabei auf 2 Nachkommastellen genau.

Anhand des Würfels und der gegebenen Seitenlänge a kannst du alle Größen herausfinden, die du zur Berechnung benötigst. Du brauchst die Seitenlänge der Grundfläche, sowie die Höhe der Pyramide.

Du benötigst den Satz des Pythagoras zur Berechnung der Seitenlänge.

Die orangene Strecke ist 4,24cm lang.