Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden konstruieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 77: | Zeile 77: | ||
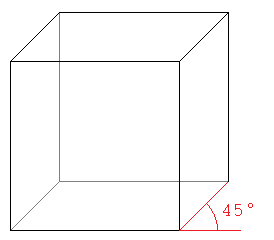
So zeichnest du ein Schrägbild einer Pyramide mit quadratischer Grundfläche. Beginne mit der Grundfläche. Zeichne diese wie gewohnt, die Kanten jedoch, die in die Tiefe (der Blattebene) zeigen sind sind nur halbsogroß, wie die in der Breite. Außerdem wichtig, die Kanten stehen in einem 45 Grad Winkel zueinander. Dieser Winkel wird auch Verzerrungswinkel genannt. Dabei bleibt die Vorderansicht unverändert. Die Seiten- und die Deckfläche werden hingegen verkürzt gezeichnet. Die schräg nach hinten laufenden Kanten sind auch kürzer als im Original. Parallele Kanten bleiben aber parallel. | So zeichnest du ein Schrägbild einer Pyramide mit quadratischer Grundfläche. Beginne mit der Grundfläche. Zeichne diese wie gewohnt, die Kanten jedoch, die in die Tiefe (der Blattebene) zeigen sind sind nur halbsogroß, wie die in der Breite. Außerdem wichtig, die Kanten stehen in einem 45 Grad Winkel zueinander. Dieser Winkel wird auch Verzerrungswinkel genannt. Dabei bleibt die Vorderansicht unverändert. Die Seiten- und die Deckfläche werden hingegen verkürzt gezeichnet. Die schräg nach hinten laufenden Kanten sind auch kürzer als im Original. Parallele Kanten bleiben aber parallel. | ||
|3=Merksatz}} | |3=Merksatz}} | ||
[[Datei:Schrägbild Würfel.png|zentriert|mini]] | |||
'''3.1. Pyramide mit quadratischer Grundfläche''' | '''3.1. Pyramide mit quadratischer Grundfläche''' | ||
Version vom 21. Oktober 2022, 07:06 Uhr
Dieser Lernpfad befindet sich aktuell im Aufbau.
.
Pyramiden konstruieren
Wie ihr im letzten Kapitel schon gelernt habt, Begegnen uns Pyramiden sehr oft im Alltag.
Fallen euch konkrete Beispiele ein?
In diesem Kapitel lernst du Netze und Schrägbilder kennen.
Beides findet unter anderem in der Architektur und dem Bauingenieurwesen Anwendung.
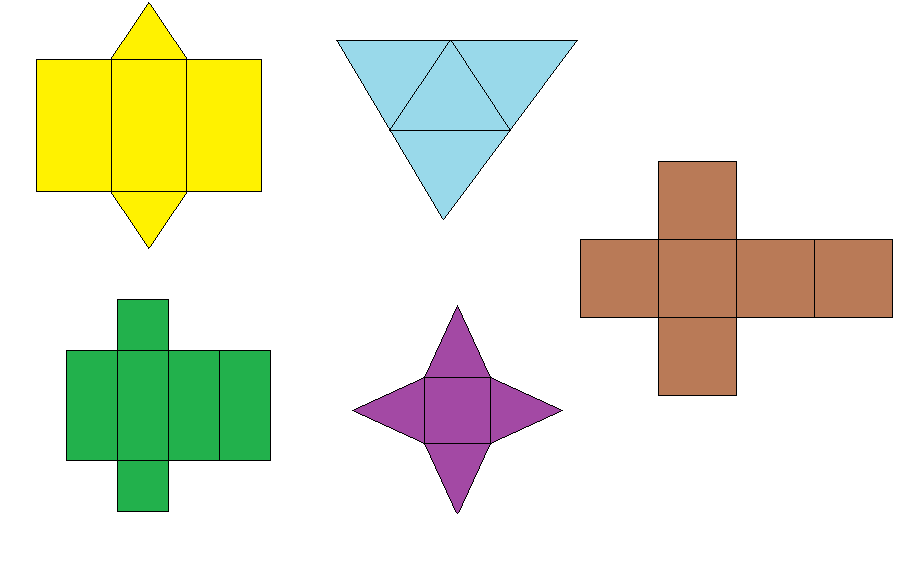
0. Netze zuordnen
Das Netz eines Körpers dient dazu, dessen Flächen (perspektivisch unverzerrt) in der Ebene darzustell
Versch. Pyramiden/Körper: Netze zuordnen? Wo tauchen die Maße der Pyramide im Netz wieder auf? SuS mehr entdecken lassen, weniger vorgeben
===1. Netze entwerfen=== NOTATION AUS DEM SCHULBUCH!
1.1. Pyramide mit quadratischer Grundfläche
Ziel: Schritt für Schritt das Netz einer Pyramide mit quadratischer Grundfläche erstellen a) Zeichne zuerst ein Quadrat.
b) Zeichne als nächstes die Diagonalen in das Quadrat ein. Der Schnittpunkt der Diagonalen kennzeichnest du mit einem "S". (Verwirrende Bezeichnung "S"?)
c) Markiere nun auf den Seiten des Quadrats die Punkte, die auf der Mitte der Seiten liegen, indem du folgendes für alle vier Seiten tust: Lege das Geo-Dreieck so, dass eine Gerade entsteht, die durch S und senkrecht durch die jeweilige Seite verläuft. Somit erhältst du die Punkte, die mittig auf den Seiten liegen. Trage diese Punkte ab und nenne sie A, B, C bzw. D.
d) Zeichne nun, von den vier mittig auf den Seiten liegenden Punkten A bis D ausgehend, jeweils eine 4cm-lange Strecke ein; diese beginnt jeweils in den Punkten A (bzw. B, C, D), steht senkrecht auf der jeweiligen Seite des Quadrats und führt vom Quadrat weg. (Bezeichnung der Punkte?)
e) Verbinde nun die "Enden" der soeben erstellten Strecken mit den nächstliegenden Ecken des Quadrats, sodass vier Dreiecke entstehen, die das Quadrat umschließen.
1.2. Tetreader
...
2. Körper herstellen
Du hast schon Netze kennengelernt. Überlege dir nun, wie du daraus einen Körper erstellen kannst.

2.1. Pyramide mit quadratischer Grundfläche
Ziel: aus dem Aufgabe 1.1. erstellten Netz einen Körper basteln a) Nimm das Netz, was du in Aufgabe 1.1 erstellt hast und lege es vor dich hin. Falls du diese Aufgabe übersprungen hast, gehe zurück und zeichne ein Netz.
b) Schneide das Netz aus.
c) Falte die Seitenflächen entlang der Kanten des Quadrats, jeweils an den Punkten A,B,C und D.
d) Jetzt kannst du die Seitenflächen an der oberen Spitze zusammenfügen. Das ist dann die Spitze deiner Pyramide.
e) Du kannst deine Pyramide an den Seiten mit etwas Tesafilm fixieren, wenn du möchtest.
2.2. Tetraeder erkunden
Implementierung von Applet wie Geogebra: Pyramide zeichnen (3D), mit Regler so verschieben, dass es Tetraeder wird: Was fällt euch auf.
Idee: Ecken der Grundflächen mit Regler verändern.
3. Schrägbilder skizzieren
3.1. Pyramide mit quadratischer Grundfläche
Ziel: die räumliche Zeichnung (also das Schrägbild) einer Pyramide mit quadratischer Grundfläche anfertigen
a) Zeichne das Schrägbild eines Quaders.
b) Zeichne auf der Fläche, der der Grundfläche gegenüberliegt (sozusagen die "Dachfläche") die beiden Diagonalen ein. Bezeichne deren Schnittpunkt mit S.
c) Verbinde S mit den unteren vier Ecken des Quaders.
3.2. Pyramide mit n-eckiger Grundfläche
Ziel: das Schrägbild einer Pyramide mit n-eckiger Grundfläche anfertigen
a) Überlege dir, welche Grundfläche deine Pyramide haben soll (Bsp.: dreieckige, quadratische, sechseckige Grundfläche).
b) ("Stützendes Schrägbild", z.B. Quader, vllt doch ungeeignet?)
4 Sicherung
Lückentext zu Fachinhalten wie Netz, Seitenfläche,…